«Математика стрелок»
Вероятно, вам известен вопрос-шутка: «Как правильнее сказать: три да четыре суть пять или три да четыре есть пять?» И когда под веселый смех окружающих вопрошаемый выбирает второй вариант, вы, к его великому смущению, напоминаете, что согласно арифметике три да четыре будет семь, а не пять. Спрашиваемый попал в ловушку, так как подчеркнутой интонацией слов «суть» и «есть» его внимание было отвлечено от арифметики в сторону грамматики.
Но подождите торжествовать, сейчас и вы узнаете, что три да четыре не всегда в сумме дает семь,
Дело в том, что величины бывают скалярные и векторные. Первые характеризуются только числом, например длина, объем, время. Вторые характеризуются не только числом, но и направлением.
Скалярные величины складываются арифметически (три кубических метра да четыре кубических метра всегда будет семь кубических метров) . Векторные величины складываются геометрически.
Поясним это на простом примере (см. рис. 1). Поперек реки плывет лодка. Если бы вода в реке была неподвижна, то лодка перемещалась бы каждую секунду, например, на |AB| = 4 м. В действительности же вода в реке течет и сносит лодку по течению за то же время, скажем, на |AD| = 3 м. В результате лодка оказывается в точке C. Каково будет перемещение лодки за секунду по отношению к берегу в текущей воде?
Перемещение есть величина векторная. В самом деле, ведь важно знать не только расстояние, на которое сместится лодка, но и направление перемещения.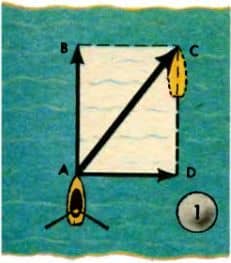 
Искомое перемещение лодки показано на рисунке 1 отрезком AC.
Вектор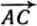 
есть сумма векторов 
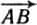и 
: 
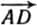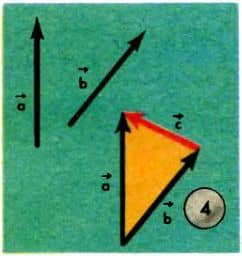Над векторными величинами в отличие от скалярных принято ставить стрелку.
На чертеже векторы обозначают не простым отрезком, а отрезком направленным — в виде стрелки, указывающей, куда направлен вектор. Поскольку в рассматриваемом примере слагаемые векторы направлены под прямым углом друг к другу, то для нахождения длины результирующего вектора можно воспользоваться известной теоремой Пифагора. Таким образом,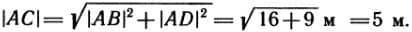 
На рисунке 1 показано сложение векторов по правилу параллелограмма.
Слагаемые векторы являются сторонами параллелограмма, а результирующий вектор есть диагональ параллелограмма. Сложение векторов можно производить и иначе — по правилу треугольника. Такой способ сложения векторов показан на рисунке 2. К концу вектора 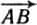приставляют начало вектора 
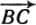и затем соединяют вектором 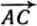начало первого вектора с концом второго. Вектор 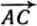есть сумма векторов 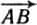и 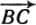. Нетрудно сообразить, что оба правила сложения векторов приводят к одному и тому же результату.
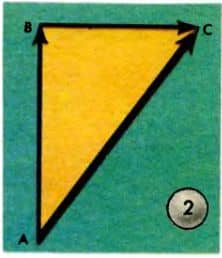На рисунках 1 и 2 угол между слагаемыми векторами равнялся 90°. В общем случае угол между слагаемыми векторами может быть каким угодно. Чем меньше этот угол, тем, очевидно, больше длина результирующего вектора (при заданных длинах слагаемых векторов). Если рассматриваемый угол равен нулю, длина результирующего вектора максимальна; она равна арифметической сумме длин слагаемых векторов.
Если же этот угол равен 180° (слагаемые векторы направлены в противоположные стороны), длина результирующего вектора минимальна; она равна арифметической разности длин слагаемых векторов. При этом результирующий вектор направлен в сторону вектора большей длины.
Для лучшего закрепления сказанного о сложении векторов представим ту же задачу в такой форме. Пловец пытается быстро переплыть реку шириной 200 м. Скорость пловца в стоячей воде равна 20 м/мин. Пловец старался плыть перпендикулярно течению, но течение реки каждую минуту относило его на 12 м от цели. Поэтому он достигает противоположного берега в точке C (рис. 3, а).
Если же пловец будет стремиться плыть под некоторым углом к линии AB так, что течение все время будет сносить его на эту линию, то, плывя с той же скоростью по отношению к воде, он окажется в конце концов в точке B (рис. 3, б). В каком случае пловец скорее достигнет противоположного берега?
Рассчитав, вы, к своему удивлению, получите такие ответы: в первом случае переправа займет 10 мин, а во втором 12,5 мин. Кратчайшая дорога не всегда скорейшая!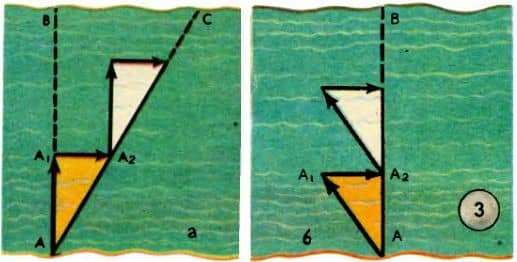 
В следующей беседе нам понадобится умение вычитать векторы.
Покажем, как это надо делать (см. рис. 4). Пусть из вектора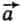 
надо вычесть вектор 
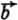. Приставьте начало вектора 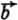к началу вектора 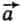, сохраняя, конечно, их направления. Затем проведите вектор 
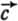от конца вектора 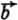(вычитаемого) к концу вектора 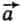(уменьшаемого).
Полученный вектор 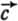и есть разность векторов 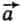и 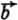, в чем легко убедиться, проверив вычитание сложением: 
(1 votes, average: 5,00 out of 5)