Механические колебания
Колебания являются очень распространенным видом движения. Это покачивание веток деревьев на ветру, вибрация струн у музыкальных инструментов, движение поршня в цилиндре двигателя автомобиля, качания маятника в настенных часах и даже биения нашего сердца.
Рассмотрим колебательное движение на примере двух маятников — нитяного и пружинного.
Нитяной маятник изображен на рисунке 30. Он представляет собой шарик, прикрепленный к тонкой, легкой нити. Если этот шарик сместить в сторону от положения равновесия и отпустить, то он начнет Колебаться,
На рисунке 31 изображен пружинный маятник. Он представляет собой груз, способный колебаться под действием силы упругости пружины.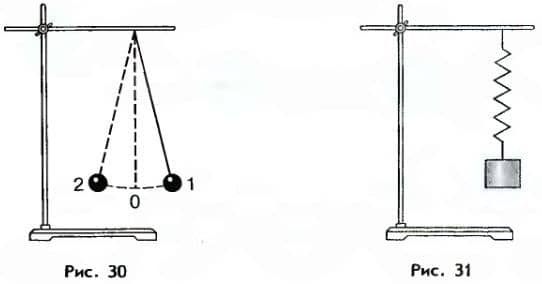 
Колебательное движение характеризуют амплитудой, периодом и частотой колебаний:
A — амплитуда; T — период; ν — частота.
Амплитуда колебаний — это максимальное расстояние, на которое удаляется колеблющееся тело от своего положения равновесия. Амплитуда колебаний измеряется в единицах длины — метрах, сантиметрах и т. д.
Период колебаний — это время, за которое совершается одно колебание. Период колебаний измеряется в единицах времени — секундах, минутах и т. д.
Частота колебаний — это число колебаний, совершаемых за 1 с. Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний равна 1 Гц, то это означает, что за каждую секунду совершается одно колебание.
Если же, например, частота ν = 50 Гц, то это означает, что за каждую секунду совершается 50 колебаний.
Для периода T и частоты ν колебаний справедливы те же формулы, что и для периода и частоты обращения, которые рассматривались при изучении равномерного движения по окружности (см. § 6).
1. Чтобы найти период колебаний, надо время t, за которое совершено несколько колебаний, разделить на число n этих колебаний: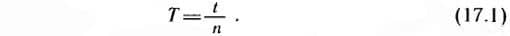 
2. Чтобы найти частоту колебаний, надо число колебаний разделить на время, в течение которого они произошли: 
При подсчете числа колебаний на практике следует четко понимать, что представляет собой одно (полное) колебание. Если, например, маятник начинает двигаться из положения 1 (см. рис. 30), то одним колебанием является такое его движение, когда он, пройдя положение равновесия 0, а затем крайнее положение 2, возвращается через положение равновесия 0 снова в положение 1.
Сравнивая формулы (17.1) и (17.2), мы видим, что период и частота колебаний — величины взаимно обратные, т. е.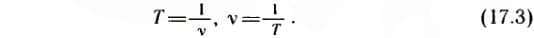 
В процессе колебаний положение тела непрерывно меняется. График зависимости координаты колеблющегося тела от времени называют Графиком колебаний. По горизонтальной оси на этом графике откладывают время t, по вертикальной — координату x. Модуль этой координаты показывает, на каком расстоянии от положения равновесия находится колеблющееся тело (материальная точка) в данный момент времени.
При переходе тела через положение равновесия знак координаты меняется на противоположный, указывая тем самым, что тело оказалось по другую сторону от среднего положения.
О форме графика колебаний можно судить на основе следующих опытов.
Соединим пружинный маятник с пишущим устройством (например, кисточкой) и начнем перед колеблющимся телом равномерно перемещать бумажную ленту (рис. 32). Кисточка нарисует на ленте линию, которая по форме будет совпадать с графиком колебаний.
Для записи колебаний нитяного маятника можно воспользоваться установкой, изображенной на рисунке 33. Маятником здесь служит воронка с песком. Если под колеблющейся воронкой перемещать бумажную ленту (или деревянную доску), высыпающийся из воронки песок оставит на ней характерный след.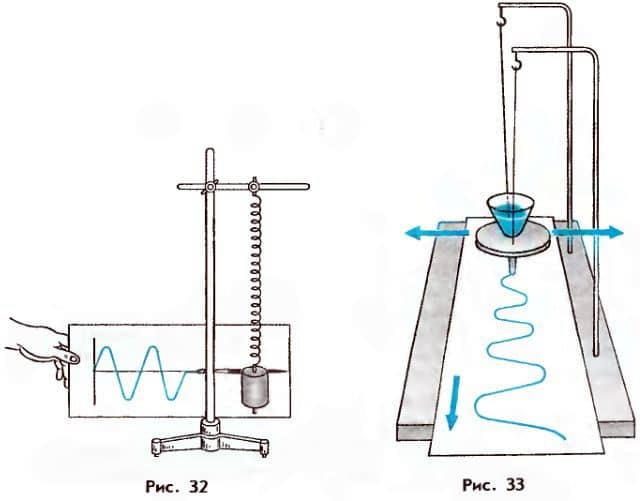 
При достаточно малом трении и на протяжении небольших интервалов времени графиком колебаний каждого из маятников является синусоидальная кривая, или кратко синусоида.
По графику колебаний можно определить все характеристики колебательного движения. Так, например, график, изображенный на рисунке 34, описывает колебания с амплитудой A=5 см, периодом F=4 с и частотой ν = 1/T = 0,25 Гц.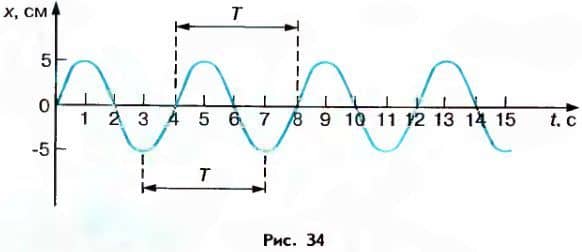 
1. Приведите примеры колебаний. 2. Что называют амплитудой колебаний? 3. Что такое период колебаний?
4. Что называют частотой колебаний? 5. Как называется единица частоты колебаний? 6. Чем отличается пружинный маятник от нитяного?
7. Какая сила заставляет опускаться нитяной маятник после того, как он был выведен из положения равновесия? Почему он не останавливается в положении равновесия? 8. Под действием какой силы происходят колебания пружинного маятника?
(1 votes, average: 5,00 out of 5)