Относительное движение брошенных тел. Отскок от наклонной плоскости
1. Относительное движение брошенных тел
Пусть в некоторый момент (t = 0) из точки A на высоте h начинает падать яблоко (рис. 12.1). Лежащий на траве юный стрелок в тот же момент стреляет из пружинного пистолета, намереваясь попасть «в яблочко».
Пистолет находится в точке B на расстоянии d от вертикали, вдоль которой падает яблоко, а скорость пули по модулю равна v0.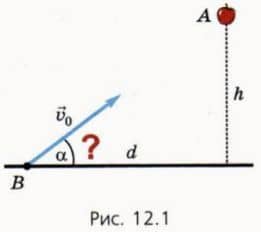 
1) Под каким углом а к горизонту надо направить пулю?
2) В какой момент времени пуля попадет в яблоко?
Найдем сначала ответы на эти вопросы
? 1. Объясните, почему пуля может попасть в яблоко при условии, что
Tg α = h/d. (1)
Эта удивительно простая формула утверждает, что целиться надо точно в яблочко — так, будто ни пуля, ни яблоко не чувствуют притяжения Земли! Для того чтобы пуля попала в яблоко, значение имеет (казалось бы) только направление ее начальной скорости.
? 2. Объясните, почему до попадания пули в яблоко они будут двигаться в течение времени
T = AB/v0. (2)
Здесь AB = √(d2 + h2) — расстояние между пулей и яблоком в начальный момент.
Подсказка. Воспользуйтесь тем, что t = d/v0x = d/(v0cos α).
Формула (2) тоже замечательна своей простотой: как будто бы яблоко и правда замерло на месте в ожидании пули, а пуля летела к яблоку, не чувствуя земного притяжения!
Найдем теперь физическую разгадку этой «простоты» и покажем, как можно было найти угол α и время полета устно.
Поскольку яблоко и пуля движутся с ускорением свободного падения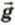 
, их скорости в момент времени t в векторном виде выражаются формулами 
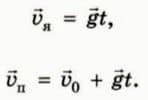Перейдем в систему отсчета, связанную с яблоком.
Скорость яблока в этой системе отсчета остается равной нулю, а скорость пули относительно яблока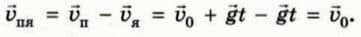 
Итак, до попадания в яблоко пуля движется относительно яблока с постоянной скоростью 
0, то есть прямолинейно и равномерно!
Вот почему целиться надо «точно в яблочко», и вот почему время полета пули до попадания в яблоко равно начальному расстоянию между ними, деленному на начальную скорость пули! Мы видим, что полученные выше формулы (1), (2) можно было записать сразу, без вычислений.
Остается проверить: действительно ли модуль начальной скорости пули не имеет значения для попадания в яблоко?
? 3. При какой начальной скорости пули она может попасть в яблоко?
Подсказка. Время полета пули до попадания в яблоко должно быть меньше времени падения яблока на землю.
Докажем, что тела, брошенные под любыми углами к горизонту с любыми начальными скоростями, движутся друг относительно друга с постоянной (по модулю и по направлению) скоростью, то есть прямолинейно равномерно.
Действительно, пусть начальные скорости двух тел равны 01 и 02. Тогда их скорости в момент времени t выражаются в векторном виде формулами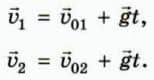 
Скорость второго тела относительно первого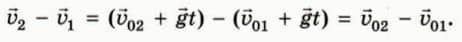 
Эта формула показывает, что относительная скорость тел не зависит от времени, то есть тела движутся друг относительно друга с постоянной скоростью.
Свидетелями этого интересного явления мы становимся, наблюдая во время фейерверков за разноцветными огненными шарами (рис. 12.2). 
Они имеют форму шаров именно потому, что образующие их светящиеся ракеты движутся друг относительно друга с постоянными скоростями! Знание «секрета» относительного движения брошенных тел позволяет легко решать задачи, кажущиеся на первый взгляд довольно трудными.
? 4. Из одной точки одновременно бросили два тела — первое под углом 15º к горизонту, а второе — под углом 75º к горизонту. Начальная скорость каждого тела 20 м/с. Траектории тел лежат в одной плоскости.
Попробуйте на все следующие вопросы (кроме а) ответить устно. а) Изобразите на одном чертеже начальные скорости тел и найдите начальную скорость второго тела относительно первого. Чему она равна по модулю? б) Будет ли эта относительная скорость изменяться во время полета тел? в) Какой формулой в единицах СИ выражается зависимость расстояния d между телами во время полета?
г) Через какой промежуток времени после броска расстояние между движущимися телами стало равным 10 м? д) Объясните, почему эти тела не могут столкнуться в полете.
2. Отскок мяча от наклонной плоскости
Мяч свободно падает без начальной скорости с высоты h на наклонную плоскость с углом наклона α, отскакивает от нее и затем снова ударяется о плоскость (рис. 12.3).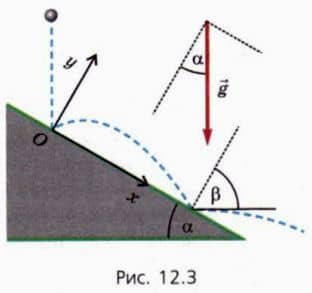 
Будем считать, что в результате столкновения мяча с плоскостью модуль скорости мяча не изменяется, а угол отражения равен углу падения. (Углы падения и отражения — это углы между скоростью мяча и перпендикуляром к наклонной плоскости непосредственно перед ударом мяча о плоскость и после удара.)
Выясним: 1) чему равен промежуток времени τ между ударами? 2) чему равно расстояние d между точками ударов?
Обычно при рассмотрении ситуаций, в которых речь идет о наклонной плоскости, удобно направить ось x вдоль наклонной плоскости вниз, а ось y — перпендикулярно наклонной плоскости вверх (см. рис. 12.3).
Обозначим 0 скорость мяча непосредственно перед первым ударом о плоскость, а 1 — скорость сразу после удара. Угол отражения мяча от наклонной плоскости после первого удара равен α, а угол отражения после второго удара мы обозначим β (мы его тоже найдем).
? 5. Объясните, почему зависимость проекций скорости мяча от времени между ударами задается уравнениями
Vx = vx1 + gxt = (v0 + gt) sin α, vy = vy1 + gyt = (v0 — gt) cos α.
? 6. Объясните, почему зависимость координат мяча от времени между ударами задается уравнениями
X = vx1t + gxt2/2 = (v0 + gt/2)t sin α; y = vy1t + gyt2/2 = (v0 — gt/2)t cos α.
? 7. Получите формулу для промежутка времени τ между первым и вторым ударами мяча о плоскость:
Τ = 2(v0/g).
Подсказка. Воспользуйтесь тем, что при ударе мяча о плоскость координата мяча y = 0.
Итак, промежуток времени между ударами не зависит от угла наклона плоскости α! Он определяется только модулем скорости в момент падения мяча, то есть начальной высотой h.
? 8. Выразите расстояние d между точками первых двух ударов мяча о плоскость через v0, α и g.
? 9. Объясните, почему расстояние между точками второго и третьего ударов мяча о плоскость равно 2d.
? 10.Расстояния между точками последовательных ударов мяча о плоскость относятся, как 1 : 2 : 3 : 4…. Объясните, как получается это отношение.
Найдем соотношение между углом наклона плоскости α и углом β отражения мяча после второго удара (рис. 12.3).
Для этого надо найти проекции скорости мяча сразу после второго удара о плоскость.
? 11.Объясните, почему проекции скорости мяча сразу после второго удара о плоскость выражаются формулами
Vx = 3v0 sin α, vy = v0 cos α.
Подсказка. Воспользуйтесь тем, что в результате удара о плоскость проекция скорости мяча на ось x не изменяется, а проекция скорости на ось y изменяет знак, а также формулами зависимости проекций скорости мяча от времени и выражением для промежутка времени τ между двумя ударами.
? 12. Обоснуйте формулу
Tg β = 3tg α.
Подсказка. Воспользуйтесь тем, что сразу после второго удара
Tg β = vx/vy.
? 13.Чему равен угол наклона плоскости α, если сразу после второго удара скорость мяча направлена горизонтально?
Подсказка. Воспользуйтесь тем, что в таком случае α + β = 90º, поэтому tg β = 1/tg α.
Дополнительные вопросы и задания
В задачах этого параграфа предполагается, что сопротивлением воздуха можно пренебречь.
14. С высоты 20 м одновременно бросили горизонтально в противоположных направлениях два камешка. Начальная скорость первого 10 м/с, а второго — 20 м/с. Чему, будет равно расстояние между камешками через 1 с; 2 с; 3 с?
15. Лежащий на земле футбольный мяч после удара приобрел скорость 10 м/с под углом 45º к горизонту и ударился о вертикальную стену, находящуюся на расстоянии 3 м от начальной точки. Траектория мяча лежит в плоскости, перпендикулярной стене. Считайте, что при ударе о стену горизонтальная проекция скорости мяча изменила знак, а модуль скорости не изменился.
а) В какой момент произошел удар мяча о стену: при его подъеме или при спуске? б) На какой высоте мяч ударился о стену? в) Чему была равна скорость мяча при ударе?
г) На каком расстоянии от стены упал бы мяч, если бы он пролетел сквозь стену, не изменив скорости? д) На каком расстоянии от стены упал мяч после удара?
(1 votes, average: 5,00 out of 5)