Применение первого закона термодинамики к различным процессам
С помощью первого закона термодинамики можно делать важные заключения о характере протекающих процессов. Рассмотрим различные процессы, при которых одна из физических величин остается неизменной (изопроцессы). Пусть система представляет собой идеальный газ.
Это самый простой случай.
Изохорный процесс. При изохорном процессе объем не меняется и поэтому работа газа равна нулю. Изменение энергии согласно уравнению (4.11) равно количеству переданной теплоты:
ΔU = Q. (4.12)
Если газ нагревается, то Q > 0 и ΔU > 0, его внутренняя энергия
Изотермический процесс. При изотермическом процессе (T = const) внутренняя энергия идеального газа (4.1) не меняется. Согласно формуле (4.11) все переданное системе количество теплоты идет на совершение работы:
Q = A’. (4.13)
Если газ получает теплоту (Q > 0), то он совершает положительную работу A’ > 0. Если, напротив, газ отдаст теплоту окружающей среде (термостату), то Q < 0 и A’ < 0. Работа же внешних сил над газом в последнем случае положительна.
Изобарный процесс. При изобарном процессе согласно формуле (4.11) передаваемое системе количество теплоты идет на изменение внутренней энергии системы и совершение работы при постоянном давлении.
Если газ нагревается (Q > 0), то он расширяется и совершает положительную работу (A’ > 0).
Одновременно увеличивается его внутренняя энергия (ΔU > 0).
При охлаждении (Q > 0) газ сжимается и внешние силы совершают над ним положительную работу (A > 0), его внутренняя энергия уменьшается (ΔU < 0).
Адиабатный процесс. С рассмотренными выше изопроцессами вы ознакомились в третьей главе, до изучении первого закона термодинамики. Теперь речь пойдет о процессе, протекающем в системе, не обменивающейся теплотой с окружавшими телами.
Процесс в теплоизолированной системе называют адиабатным.
При адиабатном процессе Q = 0 и согласно (4.10) изменение внутренней энергии происходит только за счет совершении работы:
ΔU = A. (4.14)
Конечно, нельзя окружить систему оболочкой, абсолютно не допускающей теплопередачи. Но в ряде случаев можно считать реальные процессы очень близкими к адиабатным. Для этого они должны протекать достаточно быстро, так, чтобы за время процесса не произошло заметного теплообмена между системой и окружающими телами.
Согласно уравнению (4.14) при совершении над системой положительной работы, например при сжатии газа, внутренняя энергия его увеличивается. Это означает повышение температуры газа. Наоборот, при расширении сам газ совершает положительную работу (A’ > 0) и внутренняя энергия его уменьшается — газ охлаждается.
Нагревание газа при быстром сжатии можно продемонстрировать с помощью прозрачного цилиндра с плотно пригнанным поршнем (рис. 46). Если положить на дно цилиндра смоченный эфиром кусочек ватки и быстро опустить поршень вниз, то пары эфира воспламенятся.  Нагревание воздуха при быстром сжатии нашло применение в двигателях Дизеля.
Нагревание воздуха при быстром сжатии нашло применение в двигателях Дизеля.
В этих двигателях отсутствует система зажигания горючей смеси, необходимая для обычных бензиновых двигателей внутреннего сгорания. В цилиндр засасывается не горючая смесь, а атмосферный воздух. К концу такта сжатия в цилиндр с помощью специальной форсунки впрыскивается жидкое топливо (рис. 47).
К этому моменту температура воздуха так велика, что горючее воспламеняется.
При работе мощных компрессоров, сжимающих воздух, температура воздуха настолько увеличивается, что приходится прибегать к специальной системе охлаждения цилиндров. Адиабатное охлаждение газов при расширении используется в машинах для сжижения газов.
Охлаждение газа при адиабатном расширении происходит в грандиозных масштабах в атмосфере Земли. Нагретый воздух поднимается вверх и расширяется, так как атмосферное давление падает с увеличением высоты. Это расширение сопровождается значительным охлаждением.
В результате водяные пары конденсируются и образуются облака.
Теплообмен в замкнутой системе. Рассмотрим теплообмен внутри системы, состоящей из нескольких тел, имеющих первоначально различные температуры, например теплообмен между водой в сосуде и опущенным в воду горячим железным шариком. Будем считать, что система достаточно изолирована от окружающих тел и ее внутренняя энергия не меняется (замкнутая система).
Никакой работы внутри системы не совершается. Тогда согласно первому закону термодинамики (4.10) изменение энергии любого тела системы равно количеству теплоты, отданной или полученной этим телом до наступления теплового равновесия внутри системы ΔUi = Qi. Складывая подобные выражения для всех тел системы и учитывая, что суммарная внутренняя энергия не меняется (ΔU1 + ΔU2 + ΔU3 + … = 0), получим следующее уравнение:
Q1 + Q2 + Q3 + … = 0. (4.15)
Это уравнение носит название уравнения теплового баланса. Здесь Q1, Q2, Q3 … — количества теплоты, полученные или отданные телами. Эти количества теплоты выражаются формулой (4.5) или формулами (4.6), (4.7), (4.8), (4.9), если в процессе теплообмена происходят превращения вещества из жидкого состояния в газообразное или твердое (или, напротив, образуется жидкость).
Уравнение теплового баланса вначале было открыто экспериментально при наблюдении теплообмена между телами в калориметре приборе, максимально изолирующем тела от воздействий окружающей среды. С устройством калориметра вы познакомились в VII классе.
1. Как формулируется первый закон термодинамики? 2. В каких случаях изменение внутренней энергии отрицательно? 3. В каком случае работа газа будет больше: при изотермическом расширении от объема V1 до объема V2 или при изобарном расширении от объема V1 до объема V2? 4. Почему нельзя говорить, что система обладает запасом определенного количества теплоты или работы?
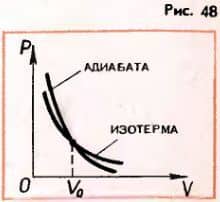
5. Какой процесс называют адиабатным? 6. На рисунке 48 изображены зависимости давления от объема при адиабатном и изотермическом процессах. Почему адиабата идет круче изотермы?
7. Запишите уравнение теплового баланса.