Расчет электрических цепей
1. Смешанное соединение проводников
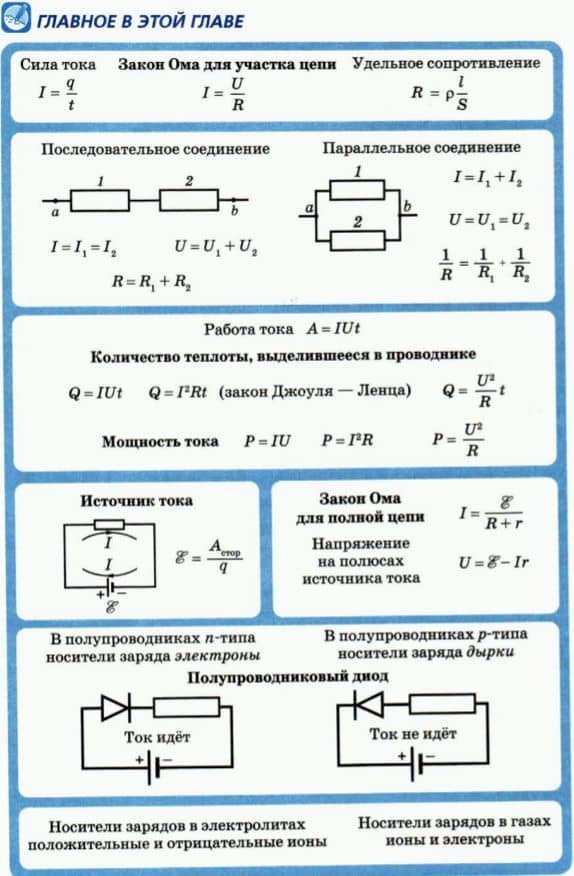
Рассмотрим электрическую схему на рисунке 61.1. Некоторые проводники в ней соединены последовательно друг с другом, а некоторые — параллельно.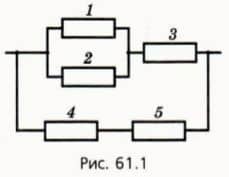 
? 1. Какие проводники в этой схеме соединены последовательно друг с другом? Какие — параллельно?
Соединение проводников, при котором часть проводников соединена последовательно друг с другом, а часть — параллельно, называют смешанным. При расчете сопротивления смешанного соединения проводников часто используют
Например, схему, изображенную на рисунке 61.1, можно преобразовать по следующему плану: 1. Заменить участок цепи с резисторами 1 и 2 одним резистором с сопротивлением, которое мы обозначим R12. 2. Заменить участок цепи, содержащий резисторы с сопротивлениями R12 и R3, одним резистором с сопротивлением, которое мы обозначим R123. 3. Заменить участок цепи с резисторами 4 и 5 одним резистором с сопротивлением, которое мы обозначим R45. 4. Заменить участок цепи с резисторами сопротивлением R123 и R45 одним резистором.
Его сопротивление и будет равно сопротивлению всего участка цепи.
? 2. В цепи, схема которой изображена на рисунке 61.1, сопротивление каждого резистора, выраженное в омах, примите равным номеру этого резистора. Начертите схемы, соответствующие каждому пункту намеченного выше плана; найдите R12, R123, R45 и сопротивление всего участка.
Не всегда с первого взгляда на электрическую схему можно распознать вид соединения проводников.
В таком случае полезно найти точки с одинаковым потенциалом (например, соединенные проводами, сопротивление которых в таких задачах считают обычно пренебрежимо малым). Затем надо перечертить схему, объединив точки с одинаковым потенциалом.
Рассмотрим, например, схему участка цепи, изображенную на рисунке 61.2.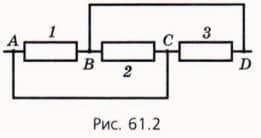 
Точки А и С соединены проводом с пренебрежимо малым сопротивлением, поэтому потенциалы этих точек равны. То же можно сказать и о точках В и D.
Следовательно, схему можно перечертить, объединив точки А и С в одну точку (обозначим ее АС), а точки В и D объединив в точку ВD. При этом, согласно исходной схеме, один конец каждого из трех резистов соединен с точкой АС, а другой — с точкой BD (рис. 61.3). 
Теперь мы видим, что резисторы соединены параллельно.
? 3. Перенесите в тетрадь рисунок 61.2 и отметьте на нем направление тока в каждом резисторе, считая, что потенциал точки А выше потенциала точки D.
? 4. На рисунке 61.4 изображена схема участка электрической цепи. Сопротивление каждого резистора, выраженное в омах, равно номеру резистора. Обратите внимание: потенциалы точек А и С различны.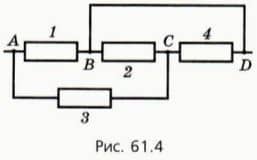 
а) Перечертите схему, изображенную на рисунке 61.4, так, чтобы легко было распознать вид соединения резисторов.
б) Найдите сопротивление всего участка цепи.
К сожалению, не всякую электрическую схему можно поэтапно упрощать, используя только формулы для последовательного и параллельного соединений. На рисунке 61.5 приведен пример схемы участка цепи, которую нельзя упростить таим образом.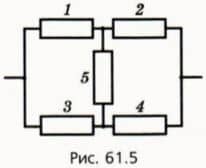 
Но для некоторых частных случав можно найти сопротивление и такого участка цепи уже известными нам способами. Чтобы догадаться, каковы эти случаи, заменим резистор 5 идеальным вольтметром (рис. 61.6). (Напомним, что идеальным считают вольтметр, сопротивление которого можно принять бесконечно большим.)
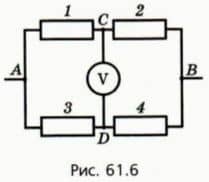
? 5. Разность потенциалов между точками А и В равна 21 В. Сопротивления резисторов, выраженные в омах, равны их номерам. а) Чему равна разность потенциалов между точками А и С? б) Чему равна разность потенциалов между точками А и D? в) Каковы показания вольтметра? г) Резистором с каким сопротивлением надо заменить резистор 4, чтобы показания вольтметра были равны нулю?
? 6. Объясните, почему показания вольтметра будут равны нулю независимо от напряжения между точками А и В, если сопротивления резисторов на схеме, изображенной на рисунке 61.6, удовлетворяют соотношению
R1/R2 = R3/R4. (1)
Схему, изображенную на рисунке 61.6, называют мостиком Уитстона. С ее помощью можно измерить сопротивление одного из четырех резисторов, подбирая сопротивления остальных трех так, чтобы выполнялось соотношение (1).
? 7. Для сопротивлений резисторов 1 — 4 в цепи, изображенной на рисунке 61.5, выполняется соотношение (1). а) Объясните, почему сопротивление данного участка цепи не зависит от сопротивления резистора 5. б) Сопротивления резисторов 1 и 3 равны соответственно 10 Ом и 15 Ом. Подберите такие значения сопротивлений резисторов 2 и 4, чтобы сопротивление всего участка было равно 24 Ом независимо от сопротивления резистора 5.
2. Максимальная мощность во внешней цепи
? 8. К источнику с ЭДС ξ и внутренним сопротивлением r подключено внешнее сопротивление R (рис. 61.7).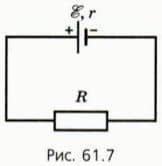 
а) Выразите мощность тока во внешней цепи через ξ, r и R. б) Используя производную, найдите, при каком R мощность тока во внешней цепи будет максимальной.
Эту задачу можно решить и без помощи производной. Для этого надо воспользоваться формулой для мощности тока во внешней цепи
P = UI,
Где U — напряжение на внешнем сопротивлении (напомним, что оно равно напряжению на полюсах источника тока), I — сила тока в цепи.
? 9. Объясните, почему мощность тока во внешней цепи выражается формулой
P = (ξ — Ir)I. (2)
Подсказка. Выразите напряжение на полюсах источника через ξ, I, r, используя закон Ома для всей цепи.
Правая часть равенства (2) представляет собой квадратичную функцию от силы тока I. Графиком ее является парабола.
? 10. Начертите график зависимости P(I) при изменении силы тока I от нуля до максимального значения (равного силе тока при коротком замыкании). а) При каком значении I достигается максимум функции P(I)?
б) Какому сопротивлению внешней цепи соответствует это значение I? Подсказка. Воспользуйтесь законом Ома для всей цепи.
Итак, максимальная мощность тока во внешней цепи достигается, когда сопротивление внешней цепи равно внутреннему сопротивлению источника тока.
? 11. Чему при этом равен КПД источника тока?
3. Конденсаторы в цепи постоянного тока
Постоянный ток не может идти через конденсатор, потому что между его обкладками находится диэлектрик. Однако между обкладками конденсатора, включенного в цепь постоянного тока, может существовать разность потенциалов, и тога конденсатор будет заряженным. Начнем с самых простых случаев, когда в цепи, помимо конденсатора, есть только один резистор.
? 12. На рисунке 61.8 изображена схема электрической цепи. ЭДС источника тока ξ = 12 В, его внутреннее сопротивление r = 2 Ом, сопротивление резистора R = 10 Ом, электроемкость конденсатора С = 2 мкФ.
61.8 а) Чему равна разность потенциалов между точками А и В? б) Чему равна разность потенциалов между точками А и D? в) Чему равен заряд конденсатора? г) Каков знак заряда обкладки конденсатора, соединенной с резистором?
? 13. На рисунке 61.9 изображена схема электрической цепи. ЭДС источника тока ξ, его внутреннее сопротивление r, сопротивление резистора R, электроемкость конденсатора C.
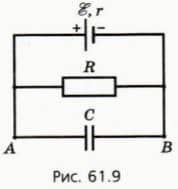а) Чему равна разность потенциалов между точками А и В? б) Чему равен заряд конденсатора?
Рассмотрим теперь более сложный случай, когда в цепи есть несколько резисторов, причем они по-разному подключены к конденсатору.
? 14. В цепи (рис. 61.10) ЭДС источника ξ = 6 В, его внутреннее сопротивление r = 1 Ом, сопротивления резисторов R1 = 3 Ом, R2 = 5 Ом, R3 = 12 Ом, электроемкость конденсатора C = 8 мкФ.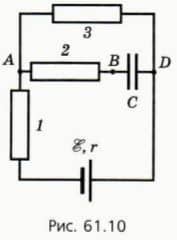 
а) Перенесите схему в тетрадь и обозначьте, через какие элементы цепи идет ток. б) Какова сила тока в резисторе 3? в) Чему равна разность потенциалов между точками А и D? г) Чему равна разность потенциалов между точками А и В? д) Чему равно напряжение на конденсаторе?
е) Чему равен заряд конденсатора? ж) Каков знак заряда обкладки конденсатора, соединенной с резистором 2?
Дополнительные вопросы и задания
15. На рисунке 61.11 изображена схема участка электрической цепи. Сопротивление каждого резистора 1 Ом. Используя метод эквивалентного преобразования схем: а) начертите схемы последовательного упрощения данной схемы, содержащие меньше резисторов; б) для каждой схемы рассчитайте ее сопротивление и найдите общее сопротивление всего участка.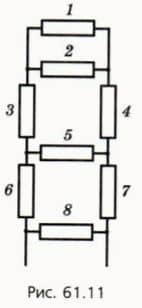 
16. На схеме участка цепи, изображенной на рисунке 61.5, сопротивления резисторов R1 = 20 Ом, R2 = 100 Ом, R3 = 10 Ом, R4 = 50 Ом, R5 = 80 Ом. Каково общее сопротивление участка цепи?
17. Сопротивление внешней цепи в 4 раза больше того значения, при котором мощность тока во внешней цепи максимальна. а) Чему равен КПД источника тока? б) Во сколько раз при этом мощность тока во внешней цепи меньше максимально возможной? 
(1 votes, average: 5,00 out of 5)