Решение задач кинематики. Задача «погоня»
Прежде чем приступить к рассмотрению конкретных задач о погоне, договоримся о следующем. Будем называть погоней ситуацию, когда два тела движутся в одном направлении друг за другом. Например, один автомобиль на прямой дороге стремится догнать другой, хищник гонится за своей добычей и т. п. Решение задачи «погоня» заключается в ответе на вопрос: может ли одно тело догнать другое, и если может, то где и когда?
Мы видим, что при решении задачи «погоня» необходимо дополнительно выяснять, может ли одно из тел догнать другое. Только в случае
Будем считать, что одно тело догнало другое, если в некоторый момент времени положения этих тел в пространстве совпали. Это означает, что в выбранной системе отсчета координаты убегающего и догоняющего тел стали равными.
Рассмотрим теперь следующую задачу о погоне. Пусть по ровному полу в сторону своей норки по прямой бежит мышка со скоростью, модуль которой |vм| = 1 м/с (рис. 25).
Вслед за мышкой вдоль этой же прямой гонится кот со скоростью, модуль которой |vк| = 3 м/с. Необходимо выяснить, удастся ли коту поймать мышку, если в тот момент, когда мы начали наблюдение, расстояние между ними составляло l1 = 6 м, а расстояние от мышки до се норки — l2 = 2 м.
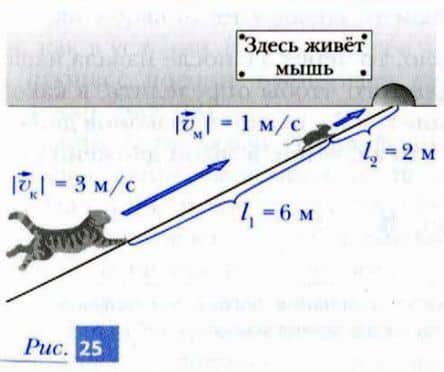
Прежде чем ответить на вопрос задачи, попробуем ответить на более простой вопрос. Представим себе, что норки нет. Тогда понятно, что кот в конце концов догонит мышку, так как его скорость больше.
Выясним, в какой момент времени (когда?) и в какой точке пространства (где?) это произойдет.
Отметим, что в этом случае последовательность действий при решении задачи «погоня» будет такой же, что и при решении задачи «встреча».
Шаг 1. Введем систему отсчета. В качестве тела отсчета выберем пол, а за начало отсчета примем место, в котором находился кот в момент начала наблюдения. Координатную ось X направим от этого места в направлении норки мыши.
В качестве единицы длины выберем 1 м. Включим часы (секундомер) в момент начала наблюдения. Эта ситуация изображена на рис. 26.
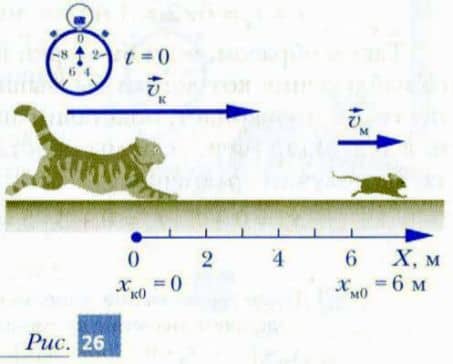Шаг 2. Определим начальные координаты движущихся тел. Ясно, что в момент включения секундомера (при t = 0) начальная координата кота xк0 = 0, а мышки — xм0 = 6 м.
Шаг 3. Определим значения скоростей равномерного движения тел. Так как и кот, и мышка движутся в положительном направлении оси X, то их координаты в нашей системе отсчета с течением времени увеличиваются. Поэтому значения скоростей обоих тел положительны. На рис. 26 мы изобразили их скорости векторами (отрезками со стрелочками на концах, показывающими направление движения).
При этом отрезок, изображающий вектор скорости кота, в три раза длиннее отрезка, изображающего вектора скорости мышки (объясните почему).
Шаг 4. Запишем в аналитическом виде зависимости координат от времени для равномерно движущихся тел (кота и мышки) с учетом известных нам начальных координат и значений скоростей. Ясно, что
Xк = xк0 + vк — t = 0 + 3 — t, xм = xм0 + vм — t = 6 + 1 — t.
Шаг 5. Представим в виде уравнения условие задачи — ситуацию, в которой при отсутствии норки кот догнал мышку в некоторый момент времени t = tд. Это означает, что в этот момент их координаты стали равны. В нашем случае условие задачи будет иметь вид:
Xк = xм.
Шаг 6. Объединим полученные выражения и присвоим им номера и названия:
Xк = xк0 + vк — t = 0 + 3 — t, (1) (закон движения кота) xм = xм0 + vм — t = 6 + 1 — t, (2) (закон движения мышки) xк = xм. (3) (условие успешного для кота завершения погони)
Шаг 7. Решение уравнений.
Подставляя выражение для xк из уравнения (1) и xм из уравнения (2) в уравнение окончания погони (3), получим:
0 + 3 — t = 6 + 1 — t.
Решим полученное уравнение.
(3 — 1) — t = 6 2 — t = 6 t = tд = 6/2 = 3 (с).
Таким образом, если бы норки не было, то через 3 с после начала нашего наблюдения кот догнал бы мышку. Для того чтобы определить, в каком месте это произойдет, подставим значение tд = 3 с в один из законов движения тел. Например, если мы подставим это значение в закон движения кота, то получим уравнение
Xк = 0 + 3 — tд = 0 + 3 — 3 = 9 (м).
Такое же значение координаты места окончания погони мы получим, если подставим значение времени tд в закон движения мышки:
Xм = 6 + 1 — tд = 6 + 1 — 3 = 9 (м).
Найденное нами значение координаты окончания погони означает, что при отсутствии норки кот поймает мышку на расстоянии 9 м от начала отсчета. Однако по условию задачи расстояние от этого места до норки равно l1 + l2 = 6 + 2 = 8 (м). Следовательно, при заданных условиях мышка достигнет точки с координатой xн = 8 м и спрячется в норке раньше, чем кот догонит ее.
Мы можем определить и тот момент времени tн когда мышка окажется в норке. Для этого, как мы уже знаем, надо записать в аналитическом виде зависимость координаты мышки от времени и условие попадания мышки в норку:
Xм = xм0 + vм — t = 6 + 1 — t, (2) (закон движения мышки) xм = xн = 8. (4) (условие попадания мышки в норку)
Для того чтобы найти момент времени tн, исходя из условия попадания мышки в норку (равенства координат мышки и ее норки), подставим выражение для xм из уравнения (2) в уравнение (4):
6 + 1 — t = 8, 1 — t = 8 — 6, t = tн = 2 (с).
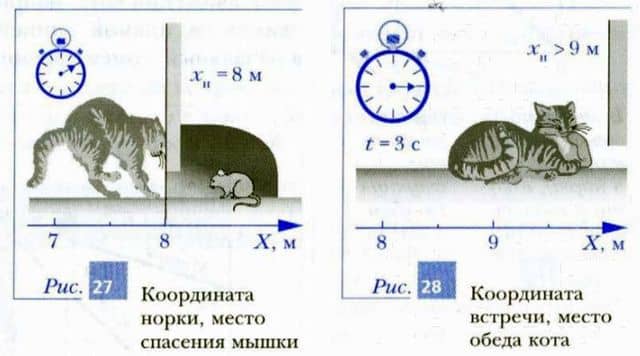
Получается, что мышка окажется в норке через 2 с после начала нашего наблюдения, т. е, на 1 с раньше, чем кот ее настигнет. Таким образом, при тех величинах, которые даны в задаче, кот останется голодным (рис. 27).
Если норка будет удалена от мышки не на 2 и, как в условии задачи, а более чем на 3 м, то процесс погони закончится для мышки плачевно (рис. 28).
Решим ту же задачу графическим методом начиная с шага 4. Напомним, что после первых трех шагов мы имеем систему отсчета, начальные координаты кота xк0 = 0 и мышки xм0 = 6 м, а также значения их скоростей vк = 3 м/с и vм = 1 м/с.
Шаг 4. Построим систему координат, состоящую из оси времени t и оси координаты X. Отметим начало отсчета и нанесем на оси метки, соответствующие единицам времени (с) и расстояния (м). Отметим на оси X начальные координаты кота xк0 = 0 и мышки xм0 = 6 м (рис. 29).
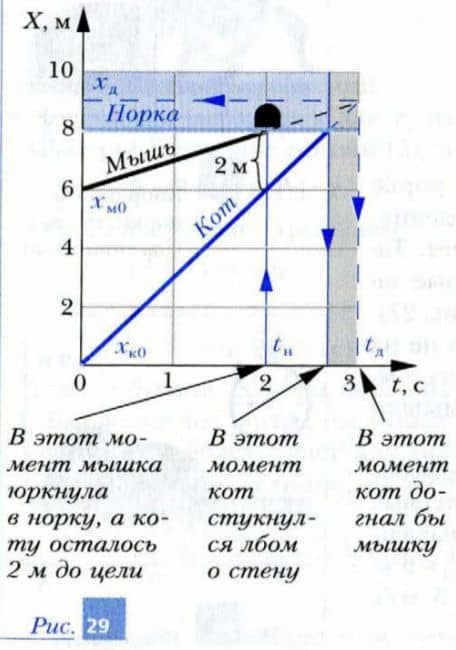Шаг 5. Так как по условию значение скорости мышки vм = 1 м/с, то ее координата с каждой секундой будет увеличиваться на 1 м. Построим несколько точек графика движения мышки для моментов времени, например, t1 = 1 с и t2 = 2 с. Ясно, что им соответствуют координаты:
Xм1 = 6 + 1 — 1 = 7 (м), xм2 = 6 + 1 — 2 = 8 (м).
Соединив эти точки, мы получим график движения мышки (см. рис. 29).
Значение скорости кота равно 3 м/с. Поэтому значение его координаты с каждой секундой увеличивается на 3 м. Построим несколько точек графика движения кота, например для моментов времени t1 = 1 с и t2 = 2 с. Соединив их прямой линией с точкой, соответствующей положению кота в начальный момент времени, получим график движения кота.
Как вы уже догадались, точка пересечения графиков движения является точкой окончания погони. Из рис. 29 видно, что кот догонит мышь через время tд = 3 с после начала наблюдения.
А произойдет это (при отсутствии норки) в точке с координатой xд = 9 м. То есть полученные нами графическим и аналитическим методами результаты совпали.
Отметим, что на рис. 29 можно изобразить и закон движения норки. Так как в нашей системе отсчета координата норки xн = 8 м не изменяется, то ее закон движения графически представляет собой прямую, параллельную оси времени. Как видно из рисунка, мышка юркнула в норку (это будет точка пересечения графиков движения мышки и норки, равенство их координат) на 1 с раньше, чем кот догонит ее.
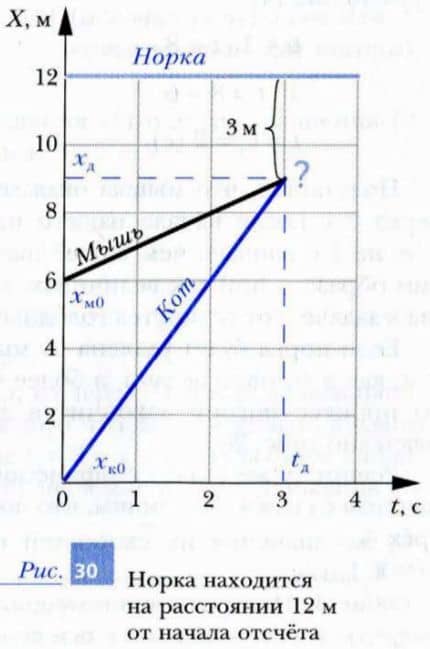
Если бы координата норки была больше координаты, в которой кот догоняет мышь, например xн1 = 12 м, то картина, как вы понимаете, выглядела бы иначе. Посмотрите на рис. 30 и объясните, что произошло бы в этом случае.
Итоги Решение задачи «погоня» заключается в ответе на вопрос: может ли одно из тел догнать другое, и если может, то в какой точке пространства и в какой момент времени это произойдет?
При аналитическом способе решения задачи «погоня» момент окончания погони и координата места погони определяются из равенства координат в законах движения тел, записанных в аналитическом виде.
Вопросы
В чем состоит отличие задачи «погоня» от задачи «встреча»? В чем их сходство? Расскажите, как по графикам движения двух тел в задаче «погоня» определить, в какой момент одно тело догонит другое.
Упражнения
Как будут выглядеть графики движения, если тела движутся друг за другом с одинаковыми скоростями 15 м/с, а в начальный момент расстояние между телами l0 = 10 м? Через какое время мотоциклист, движущийся со скоростью 100 км/ч, догонит велосипедиста, едущего в том же направлении со скоростью 20 км/ч, если в начальный момент времени расстояние между ними было равно 160 км? Лыжник юношеской сборной города Москвы, который идет со скоростью 5 м/с, отстает на 40 м от лыжника сборной города Санкт-Петербурга, который идет со скоростью 3 м/с. Кто из лыжников придет к финишу первым, если расстояние от идущего впереди лыжника до финиша равно 60 м?
(1 votes, average: 5,00 out of 5)