Силы упругости
1. Проявление сил упругости и их природа
Как вы уже знаете из курса физики основной школы, силы упругости связаны с деформацией тел, то есть изменением их формы и (или) размеров.
Связанная с силами упругости деформация тел не всегда заметна (подробнее мы остановимся на этом ниже). По этой причине свойства сил упругости изучают обычно, используя для наглядности пружины: их деформация хорошо видна на глаз.
Поставим опыт
Подвесим к пружине груз (рис. 15.1, а). (Будем считать, что массой пружины можно пренебречь.) Пружина растянется, то
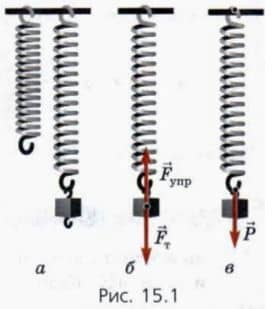
На подвешенный груз действуют сила тяжести 
Т и приложенная со стороны растянутой пружины сила упругости Упр (рис. 15.1, б). Она вызвана деформацией пружины.
Согласно третьему закону Ньютона на пружину со стороны груза действует такая же по модулю, но противоположно направленная сила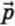 
(рис. 15.1, в). Эта сила — вес груза: ведь это сила, с которой тело растягивает вертикальный поднес (пружину).
Силы Упр и 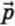, с которыми груз и пружина взаимодействуют друг с другом, связаны третьим законом Ньютона и поэтому имеют одинаковую физическую природу. Следовательно, вес — это тоже сила упругости. (Действующая на пружину со стороны груза сила упругости (вес груза) обусловлена деформацией груза. Эта деформация незаметна, если грузом является гиря или брусок. Чтобы деформация груза стала тоже заметной, можно в качестве груза взять массивную пружину: мы увидим, что она растянется.) Действуя на пружину, вес груза растягивает ее, то есть является причиной ее деформации. (Во избежание недоразумений подчеркнем еще раз, что пружину, к которой подвешен груз, растягивает не приложенная к грузу сила тяжести груза, а приложенная к пружине со стороны груза сила упругости (вес груза).)
На этом примере мы видим, что силы упругости являются и следствием, и причиной упругой деформации тел: — если тело деформировано, то со стороны этого тела действуют силы упругости (например, сила Упр на рисунке 15.1, б); — если к телу приложены силы упругости (например, сила на рисунке 15.1, в), то это тело деформируется.
? 1. Какие из изображенных на рисунке 15.1 сил а) уравновешивают друг друга, если груз покоится? б) имеют одинаковую физическую природу? в) связаны третьим законом Ньютона? г) перестанут быть равными по модулю, если груз будет двигаться с ускорением, направленным вверх или вниз?
Всегда ли деформация тела заметна?
Как мы уже говорили, «коварная» особенность сил упругости состоит в том, что связанная с ними деформация тел далеко не всегда заметна.
Поставим опыт
Деформация стола, обусловленная весом лежащего на нем яблока, незаметна на глаз (рис. 15.2).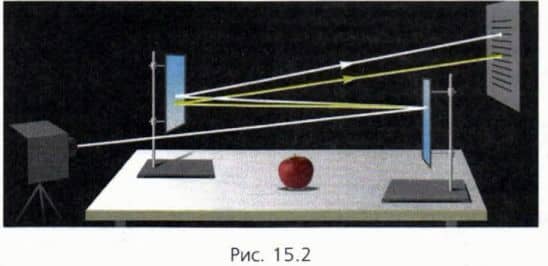 
И тем не менее она есть: только благодаря силе упругости, возникшей вследствие деформации стола, он удерживает яблоко! Деформацию стола можно обнаружить с помощью остроумного опыта. На рисунке 15.2 белые линии схематически обозначают ход луча света, когда яблока на столе нет, а желтые линии — ход луча света, когда яблоко лежит на столе.
? 2. Рассмотрите рисунок 15.2 и объясните, благодаря чему деформацию стола удалось сделать заметной.
Некоторая опасность состоит в том, что, не заметив деформации, можно не заметить и связанной с ней силы упругости!
Так, в условиях некоторых задач фигурирует «нерастяжимая нить». Под этими словами подразумевают, что можно пренебречь только величиной деформации нити (увеличением ее длины), но нельзя пренебрегать силами упругости, приложенными к нити или действующими со стороны нити. На самом деле «абсолютно нерастяжимых нитей» нет: точные измерения показывают, что любая нить хоть немного, но растягивается.
Например, если в описанном выше опыте с грузом, подвешенным к пружине (см. рис. 15.1), заменить пружину «нерастяжимой нитью», то под весом груза нить растянется, хотя ее деформация и будет незаметной. А следовательно, будут присутствовать и все рассмотренные силы упругости.
Роль силы упругости пружины будет играть сила натяжения нити, направленная вдоль нити.
? 3. Сделайте чертежи, соответствующие рисунку 15.1 (а, б, в), заменив пружину нерастяжимой нитью. Обозначьте на чертежах силы, действующие на нить и на груз.
? 4. Два человека тянут в противоположные стороны веревку с силой 100 Н каждый. а) Чему равна сила натяжения веревки? б) Изменится ли сила натяжения веревки, если один ее конец привязать к дереву, а за другой конец тянуть с силой 100 Н?
Природа сил упругости
Силы упругости обусловлены силами взаимодействия частиц, из которых состоит тело (молекул или атомов). Когда тело деформируют (изменяют его размеры или форму), расстояния между частицами изменяются. Вследствие этого между частицами возникают силы, стремящиеся вернуть тело в недеформированное состояние.
Это и есть силы упругости.
2. Закон Гука
Поставим опыт
Будем подвешивать к пружине одинаковые гирьки. Мы заметим, что удлинение пружины пропорционально числу гирек (рис. 15.3).
Это означает, что деформация пружины прямо пропорциональна силе упругости.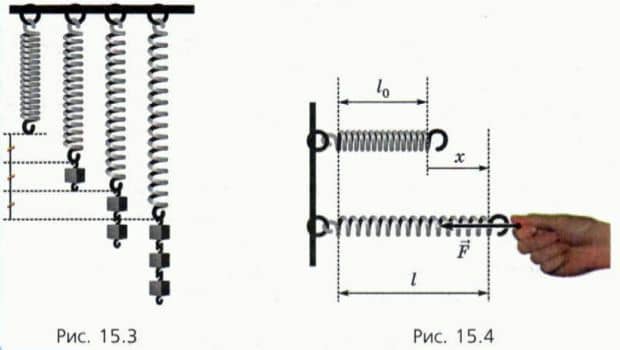 
Обозначим деформацию (удлинение) пружины
X = l — l0, (1)
Где l — длина деформированной пружины, а l0 — длина недеформированной пружины (рис. 15.4). Когда пружина растянута, x > 0, а проекция действующей со стороны пружины силы упругости Fx < 0. Следовательно,
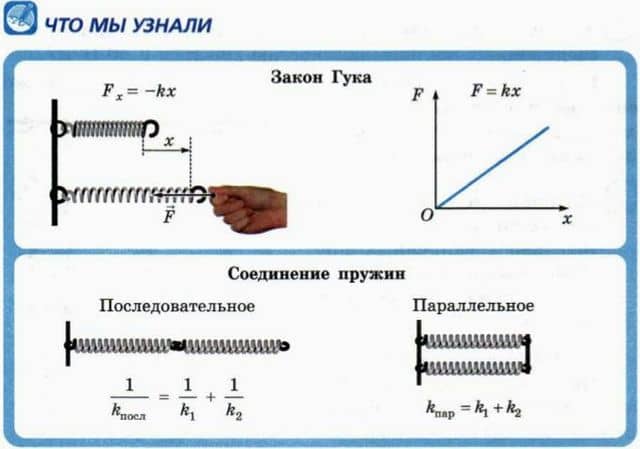
Fx = — kx. (2)
Знак «минус» в этой формуле напоминает, что приложенная со стороны деформированного тела сила упругости направлена противоположно деформации этого тела: растянутая пружина стремится сжаться, а сжатая — растянуться.
Коэффициент k называют жесткостью пружины. Жесткость зависит от материала пружины, ее размеров и формы. Единица жесткости 1 Н/м.
Соотношение (2) называют законом Гука в честь английского физика Роберта Гука, открывшего эту закономерность. Закон Гука справедлив при не слишком большой деформации (величина допустимой деформации зависит от материала, из которого изготовлено тело).
Формула (2) показывает, что модуль силы упругости F связан с модулем деформации x соотношением
F = kx. (3)
Из этой формулы следует, что график зависимости F(x) — отрезок прямой, проходящий через начало координат.
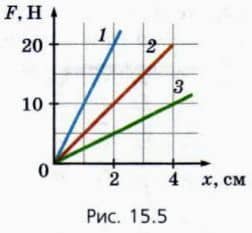
? 5. На рисунке 15.5 приведены графики зависимости модуля силы упругости от модуля деформации для трех пружин. а) У какой пружины наибольшая жесткость? б) Чему равна жесткость самой мягкой пружины?
? 6. Груз какой массы надо подвесить к пружине жесткостью 500 Н/м, чтобы удлинение пружины стало равным 3 см?
Важно отличать удлинение пружины x от ее длины l. Различие между ними показывает формула (1).
? 7. Когда к пружине подвешен груз массой 2 кг, ее длина равна 14 см, а когда подвешен груз массой 4 кг, длина пружины равна 16 см. а) Чему равна жесткость пружины? б) Чему равна длина недеформированной пружины?
3. Соединение пружин
Последовательное соединение
Возьмем одну пружину жесткостью k (рис, 15.6, а). Если растягивать ее силой (рис. 15.6, б), ее удлинение выражается формулой
X = F/k.
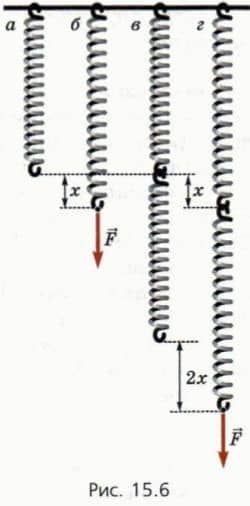Возьмем теперь вторую такую же пружину и соединим пружины, как показано на рисунке 15.6, в. В таком случае говорят, что пружины соединены последовательно.
Найдем жесткость kпосл системы из двух последовательно соединенных пружин.
Если растягивать систему пружин силой , то сила упругости каждой пружины будет равна по модулю F. Общее же удлинение системы пружин будет равно 2x, потому что каждая пружина удлинится на x (рис. 15.6, г).
Следовательно,
Kпосл = F/(2x) = ½ F/x = k/2,
Где k — жесткость одной пружины.
Итак, жесткость системы из двух одинаковых последовательно соединенных пружин в 2 раза меньше, чем жесткость каждой из них.
Если последовательно соединить пружины с разной жесткостью, то силы упругости пружин будут одинаковы. А общее удлинение системы пружин равно сумме удлинений пружин, каждое из которых можно рассчитать с помощью закона Гука.
? 8. Докажите, что при последовательном соединении двух пружин 1/kпосл = 1/k1 + 1/k2, (4) где k1 и k2 — жесткости пружин.
? 9. Чему равна жесткость системы двух последовательно соединенных пружин жесткостью 200 Н/м и 50 Н/м?
В этом примере жесткость системы двух последовательно соединенных пружин оказалась меньше, чем жесткость каждой пружины. Всегда ли это так?
? 10. Докажите, что жесткость системы двух последовательно соединенных пружин меньше жесткости любой из пружин, образующих систему.
Параллельное соединение
На рисунке 15.7 слева изображены параллельно соединенные одинаковые пружины.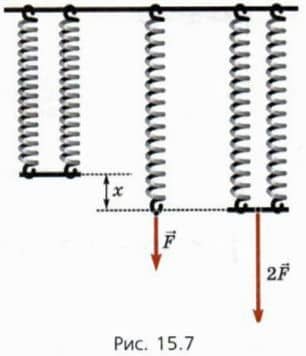 
Обозначим жесткость одной пружины k, а жесткость системы пружин kпар.
? 11. Докажите, что kпар = 2k.
Подсказка. См. рисунок 15.7.
Итак, жесткость системы из двух одинаковых параллельно соединенных пружин в 2 раза больше жесткости каждой из них.
? 12. Докажите, что при параллельном соединении двух пружин жесткостью k1 и k2
Kпар = k1 + k2. (5)
Подсказка. При параллельном соединении пружин их удлинение одинаково, а сила упругости, действующая со стороны системы пружин, равна сумме их сил упругости.
? 13. Две пружины жесткостью 200 Н/м и 50 Н/м соединены параллельно. Чему равна жесткость системы двух пружин?
? 14. Докажите, что жесткость системы двух параллельно соединенных пружин больше жесткости любой из пружин, образующих систему.
Дополнительные вопросы и задания
15. Постройте график зависимости модуля силы упругости от удлинения для пружины жесткостью 200 Н/м.
16. Тележку массой 500 г тянут по столу с помощью пружины жесткостью 300 Н/м, прикладывая силу горизонтально. Трением между колесами тележки и столом можно пренебречь. Чему равно удлинение пружины, если тележка движется с ускорением 3 м/с2?
17. К пружине жесткостью k подвешен груз массой m. Чему равно удлинение пружины, когда груз покоится?
18. Пружину жесткостью k разрезали пополам. Какова жесткость каждой из образовавшихся пружин?
19. Пружину жесткостью k разрезали на три равные части и соединили их параллельно. Какова жесткость образовавшейся системы пружин?
20. Докажите, что жесткость и последовательно соединенных одинаковых пружин в n раз меньше жесткости одной пружины.
21. Докажите, что жесткость n параллельно соединенных одинаковых пружин в n раз больше жесткости одной пружины.
22. Если две пружины соединить параллельно, то жесткость системы пружин равна 500 Н/м, а если эти же пружины соединить последовательно, то жесткость системы пружин равна 120 Н/м. Чему равна жесткость каждой пружины?
23. Находящийся на гладком столе брусок прикреплен к вертикальным упорам пружинами жесткостью 100 Н/м и 400 Н/м (рис. 15.8). В начальном состоянии пружины не деформированы.
Чему будет равна действующая на брусок сила упругости, если его сдвинуть на 2 см вправо? на 3 см влево? 
(1 votes, average: 5,00 out of 5)