Скорость прямолинейного равномерного движения
Представим себе, что мы имеем дело с равномерно движущимся по прямой велосипедистом, который проезжает за каждую секунду не 5 м (как в предыдущем параграфе), а, например, 10 м. При этом выбрана та же система отсчета. Тогда зависимость координаты фары от времени будет выглядеть несколько иначе, так как в правой части полученного нами выражения на месте числа 5 будет стоять число 10:
X = x0 + 10 * t.
Если при этом включить секундомер в момент времени, когда координата фары будет, например, x0 = 15 м, то мы получим следующее выражение:
X = 15 + 10 * t.
Как
Для этого, используя выражение x = 15 + 10 * t, найдем координаты фары велосипедиста в моменты времени t0 = 0, t1 = 1 с, t2 = 2 с и т. д. Полученные точки соединим прямой линией (рис. 16).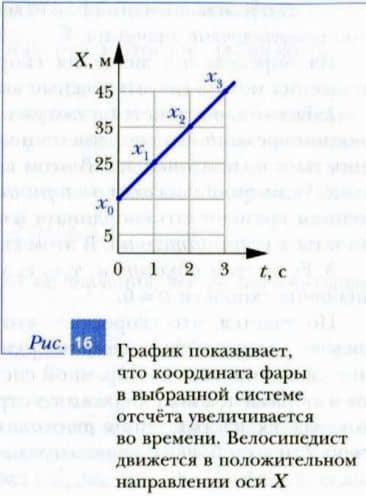 
Из этого графика видно, что начальная координата фары за каждую секунду увеличивается на 10 м. Значит, велосипедист движется в положительном направлении оси X. Если бы он ехал в отрицательном направлении оси X, то координата фары уменьшалась бы с течением времени. В этом случае изменение координаты было бы отрицательными и зависимость координаты фары от времени имела бы вид:
X = x0 — 10 * t.
Таким образом, в зависимости от направления движения изменение координаты тела (разность между значениями его координаты в последующий и предыдущий моменты времени) может быть как положительной, так и отрицательной величиной. Если же конечная и начальная координаты тела совпадают, то изменение координаты этого тела равно нулю.
В зависимости от направления движения изменение координаты тела может быть как положительной, так и отрицательной величиной.
В общем случае зависимость координаты тела от времени для прямолинейного равномерного движения имеет вид:
X = x0 + v * t.
Закон прямолинейного равномерного движения содержит постоянную величину v. Как вы понимаете, она численно равна изменению координаты тела за единицу времени.
Если тело движется равномерно прямолинейно, то физическую величину v, численно равную изменению его координаты за единицу времени, называют значением скорости равномерного прямолинейного движения.
В СИ единица скорости — метр в секунду (сокращенное обозначение — м/с).
Значение скорости показывает, насколько быстро изменяет свою координату равномерно движущееся тело, т. е. какое расстояние проходит оно за каждую секунду. В рассмотренных примерах о движении велосипедиста скорость v имела значения 5 и 10 м/с. Ясно, что для других тел она может принимать другие значения.
Ранее мы рассматривали примеры, в которых скорость муравья составляла 2 см/с. Кроме того, вы знаете, что скорость, например, автомобилей, поездов, самолетов измеряют в километрах в час (100 км/ч, 60 км/ч, 900 км/ч). Так как СИ устанавливает единицу этой физической величины метр в секунду (м/с), другие единицы могут быть приведены к общепринятой единице через коэффициенты.
Например, 1 м/с = 3,6 км/ч (если автомобиль движется по дороге со скоростью 30 м/с, то его скорость составляет 30 * 3,6 = 108 км/ч).
Из определения значения скорости равномерного прямолинейного движения можно сделать важные выводы.
Если тело движется в положительном направлении оси X, то с течением времени его координата увеличивается. Значит, изменение координаты x положительно. В этом случае значение скорости v > 0. Если тело движется в отрицательном направлении оси X, то с течением времени его координата уменьшается. Значит, изменение координаты x отрицательно. В этом случае значение скорости v < 0. Если тело покоится, т. е. его координата остается постоянной, то значение скорости v = 0.
Получается, что скорость — это величина, которая не только характеризует быстроту изменения координаты тела, но и показывает направление движения тела в выбранной системе отсчета. Поэтому скорость принято изображать в виде отрезка со стрелкой в конце. Направление стрелки совпадает с направлением движения тела.
При этом чем больше значение скорости, тем больше длина отрезка, изображающего скорость.
Величины, которые характеризуются не только числовым значением, но и направлением, называют векторными. Таким образом, скорость — вектор. Векторы обозначаются буквой со стрелкой над ней.
Например, скорость обозначают символом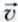 
.
Для изображения вектора скорости тела поступают следующим образом. Вначале выбирают отрезок, длина которого соответствует модулю единичной скорости 1 м/с, — единичный отрезок (рис. 17).
Теперь, чтобы изобразить скорость, равную, например, 5 м/с, нужно нарисовать отрезок, длина которого в 5 раз больше единичного. Чтобы изобразить скорость, равную 1/3 м/с, нужно начертить отрезок, длина которого в 3 раза меньше единичного. 
Число, выраженное в единицах скорости и равное отношению длины отрезка, изображающего данную скорость, к длине отрезка, изображающего единичную скорость, называют модулем скорости.
Модуль скорости 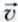принято записывать в виде |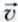|. В приведенном примере 
.
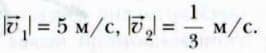Модуль скорости, в отличие от ее значения, всегда положителен или равен нулю.
Например, модуль скорости, имеющей значение -5 м/с, равен 5 м/с.
Подведем итоги.
Если значение скорости положительно, то скорость направлена в положительном направлении оси X. В этом случае ее изображают отрезком со стрелкой. Направленной в положительном направлении оси X. Так направлен вектор скорости велосипедиста на рис. 18.
Наоборот, если значение скорости отрицательно, то она направлена в отрицательном направлении оси X. Тогда ее изображают отрезком со стрелкой, направленной в отрицательном направлении оси X (вектор скорости бегуна на рис. 18).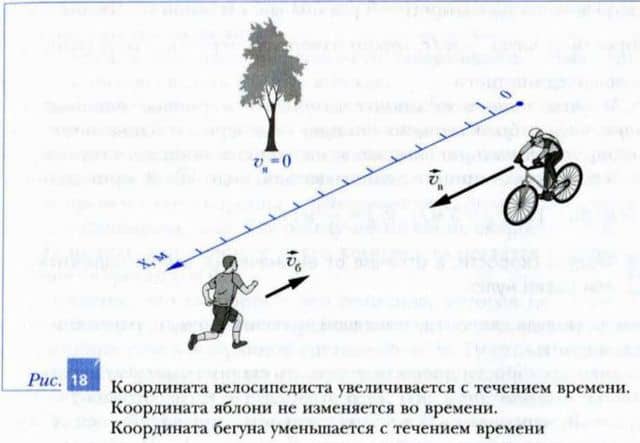 
Длины векторов изображаются на рисунке в масштабе. Так, на рис. 18 длина вектора скорости велосипедиста в два раза больше длины вектора скорости бегуна.
Поскольку скорость измеряют в метрах в секунду (м/с), длина отрезка со стрелкой (вектор скорости) не имеет отношения к расстояниям между телами, которые измеряют в метрах.
Отметим особо, что если тело покоится, то его координата в выбранной системе отсчета не изменяется. В этом случае говорят, что скорость движения тела равна нулю.
Представив закон движения тела в аналитическом виде x = x0 + v * t, в котором известны начальная координата x0 и значение скорости v, мы полностью описали прямолинейное равномерное движение тела.
Теперь можно сформулировать приведенное ранее определение равномерного прямолинейного движения иначе.
Если координата тела изменяется с течением времени по закону x = x0 + vt, при этом x0 и v не зависят от времени, то тело движется вдоль оси X равномерно.
Постоянная величина v в этом выражении равна значению скорости равномерного прямолинейного движения вдоль оси X.
Эта формулировка определения равномерного прямолинейного движения является более удобной при решении конкретных задач.
Итоги
Зависимость координаты тела от времени при равномерном прямолинейном движении имеет вид: x = x0 + vt, где x0 — начальная координата тела, v — значение скорости равномерного прямолинейного движения, t — рассматриваемый момент времени, x — координата тела в момент времени t.
Если тело движется равномерно прямолинейно, то физическую величину v, численно равную изменению его координаты за единицу времени, называют значением скорости равномерного прямолинейного движения.
В СИ единица скорости — метр в секунду (м/с).
Скорость — векторная величина, которая характеризуется не только своим модулем, но и направлением.
Если значение скорости положительно, то скорость направлена в положительном направлении оси X. Если же значение скорости отрицательно, то скорость направлена в отрицательном направлении оси X.
Вопросы
В чем заключается аналитический способ описания движения? Запишите закон прямолинейного равномерного движения в аналитической форме. Что такое значение скорости равномерного прямолинейного движения? Что оно характеризует? Что означает утверждение, что движение тела описано полностью? Приведите пример. Можно ли однозначно утверждать, что тело покоилось в течение промежутка времени от момента времени t = 0 с до момента времени t = 10 с, если изменение его координаты за этот промежуток времени равно нулю? Приведите примеры возможных ситуаций.
Упражнения
Найдите зависимости координаты тел от времени, используя для этого графики движения тел на рис. 19. Объясните, в каком направлении двигалось тело в выбранной системе отсчета в этих случаях. Движется ли тело в случае в?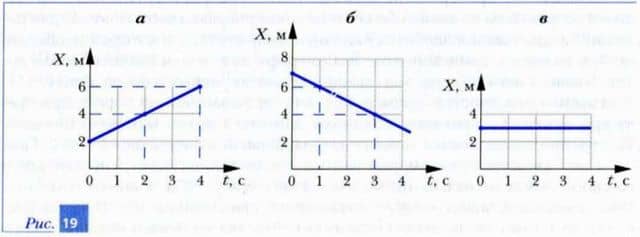 
Постройте графики движения тел, используя следующие законы движения: а) x = 3 +2t; б) x = 30 — 5t; в) x = 7. В этих законах время выражено в секундах, а расстояние — в метрах. Объясните, в какую сторону двигались тела (если двигались) в выбранной системе отсчета и на сколько изменялись их координаты за каждую секунду в упражнениях 1 и 2. Чему равны значения скоростей тел, зависимости координат которых от времени даны в упражнениях 1 и 2. Выразите в метрах в секунду значения скоростей: 3,6; 36; 72 км/ч. Выразите в километрах в час значения скоростей: 10; 20; 25 м/с. Запланируйте и проведите эксперимент по определению скорости течения ручья на его прямолинейном участке длиной 10 метров, используя закон прямолинейного равномерного движения.
(1 votes, average: 5,00 out of 5)