Сложение скоростей и переход в другую систему отсчета при движении на плоскости
1. Сложение скоростей
Пусть человек идет поперек плота, плывущего по реке. При этом скорость человека относительно плота перпендикулярна скорости течения (рис. 9.1, вид сверху).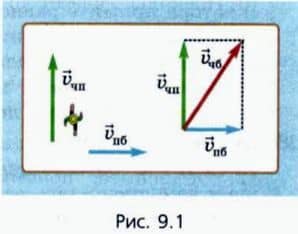 
Из правила сложения скоростей (см. § 3) следует:
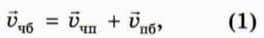где 
Чб — скорость человека относительно берега, Чп — скорость человека относительно плота,
На рисунке 9.1 справа показано, как графически найти скорость человека относительно берега (красная стрелка). Мы видим, что человек движется не перпендикулярно берегу, поскольку его (вместе с плотом) сносит течением.
Во время переправы через реку лодку тоже сносит течением. Если скорость Лв лодки относительно воды направлена перпендикулярно течению, то ее скорость Лб относительно берега (красная стрелка) будет направлена не перпендикулярно берегу, а под некоторым углом α к этому перпендикуляру (рис. 9.2).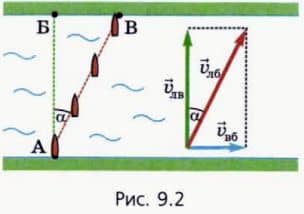 
Поэтому лодка попадет не в точку Б, находящуюся точно напротив начальной точки А, а в точку В, которая расположена ниже точки Б по течению.
На рисунке 9.2 для наглядности изображены некоторые промежуточные положения лодки, чтобы было видно, что она все время держит курс перпендикулярно берегу, но течение сносит ее во время переправы.
? 1. Моторная лодка переправляется через реку шириной 60 м. Скорость лодки относительно воды направлена перпендикулярно берегу и равна 2 м/с, а скорость течения равна 1 м/с. а) Сколько времени займет переправа? б) Насколько снесет лодку по течению за время переправы?
в) Какой угол составляет скорость лодки относительно берега с перпендикуляром к берегу?
Обратите внимание: если скорость лодки относительно воды перпендикулярна берегу, течение не влияет на время переправы.
? 2. Объясните, почему переправа через реку занимает кратчайшее время, когда скорость лодки относительно воды направлена перпендикулярно берегу (хотя при этом переправа происходит не по кратчайшему пути относительно берега).
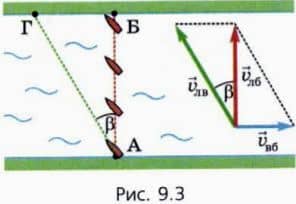
Рассмотрим теперь, как надо направить скорость лодки относительно воды, чтобы лодка попала в точку Б, расположенную точно напротив начальной точки А (рис. 9.3).
В таком случае скорость Лб лодки относительно берега должна быть перпендикулярна берегу (красная стрелка). А для этого необходимо, чтобы скорость Лв лодки относительно воды была направлена под некоторым углом β к линии АБ — немного навстречу течению.
На рисунке 9.3 изображены некоторые промежуточные положения лодки, чтобы показать, что во время переправы киль лодки остается параллельным линии АГ, где точка Г расположена выше точки Б по течению, однако течение сносит лодку так, что она попадает в точку Б.
? 3. Моторная лодка переправляется через реку шириной 60 м так, что попадает в точку Б, находящуюся точно напротив начальной точки А. Скорость лодки относительно воды равна 2 м/с, а скорость течения равна 1 м/с. а) Какой угол составляет скорость лодки относительно воды с перпендикуляром к берегу? б) Чему равна скорость лодки относительно берега?
в) Сколько времени занимает переправа?
Мы видим, что переправа по кратчайшему пути (относительно берега), занимает большее время, чем в случае, когда скорость лодки относительно воды направлена перпендикулярно берегу. Чтобы двигаться точно поперек течения, лодке приходится бороться с ним.
? 4. Может ли лодка попасть из точки А в точку Б, если ее скорость относительно воды меньше скорости течения или равна ей? Дайте пояснительный чертеж.
Итак, мы видим, что даже в случае, когда течение или ветер направлены перпендикулярно траектории лодки, корабля или самолета (относительно земли), это все-таки тормозит движение. Правда, если скорость ветра мала по сравнению со скоростью самолета, то задержка при боковом ветре существенно меньше, чем при встречном ветре той же скорости.
? 5. В безветренную погоду перелет самолета из города Л в город К занимает 1 ч. Во время полета дует ветер, скорость которого в 10 раз меньше скорости самолета относительно воздуха. Сколько времени будет длиться перелет, если ветер: а) встречный? б) перпендикулярен трассе полета?
2. Переход в другую систему отсчета
На рисунке 9.4 схематически изображено положение двух кораблей в море и показаны их скорости 1 и 2. 
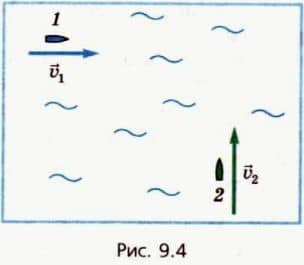
Может ли произойти столкновение этих кораблей, если они будут продолжать следовать своими курсами? А если нет, то каким будет минимальное расстояние dmin между ними?
Если рассматривать движение кораблей в системе отсчета, связанной с Землей, ситуация представляется непростой: надо следить одновременно за двумя кораблями, не пропустив момент наибольшего их сближения.
Однако эта ситуация значительно упрощается, если перейти в систему отсчета, связанную с любым из кораблей — например, с кораблем 2 (рис, 9.5).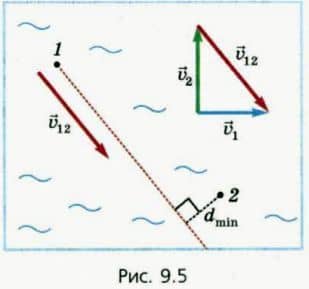 
В этой системе отсчета корабль 2 покоится, поэтому надо следить за движением только одного корабля — корабля 1. Чтобы найти его скорость 12 относительно корабля 2, нужно, как мы уже знаем, вычесть из скорости 1 скорость 2: 
В правой верхней части рисунка 9.5 показано, как графически найти скорость 12.
В системе отсчета, связанной с кораблем 2, корабль 1 движется вдоль прямой, параллельной его скорости 12 в этой системе отсчета (красный пунктир).
Мы видим, что кораблям, к счастью, столкновение не грозит. А проведя перпендикуляр из положения корабля 2 к красному пунктиру, мы найдем и минимальное расстояние между кораблями dmin.
? 6. На рисунке 9.6 изображено положение автобуса (А) и такси (Т) в некоторый момент времени и обозначены их скорости. Две клетки соответствуют 100 м или 10 м/с.
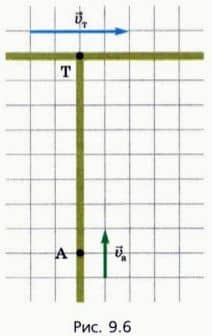Связанную с автобусом систему отсчета называем далее для краткости «система А». а) Перенесите рисунок в тетрадь и найдите графически скорость такси в системе А. б) Начертите траекторию движения такси в системе А. в) Найдите модуль скорости такси в системе А. г) Найдите графически и аналитически наименьшее расстояние между такси и автобусом.
Подсказка. Воспользуйтесь подобием треугольников скоростей и перемещений в системе А.
Дополнительные вопросы и задания
По реке плывет квадратный плот со стороной a (рис. 9.7). По периметру плота идет человек со скоростью vч относительно плота. Скорость течения равна vт.
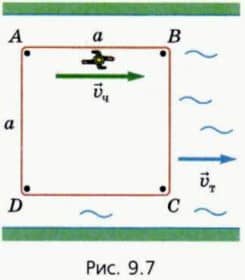а) Найдите выражение для пути, пройденного человеком относительно берега, если он двигался от А к В; от В к С; от С к D; от D к А. б) Найдите отношение пути, пройденного человеком относительно берега, к пути, пройденному им относительно плота, если: 1) vч = 2vт; 2) vч = 0,5vт.
8. Человек на моторной лодке отправляется из точки А с намерением попасть в точку В (рис. 9.8).
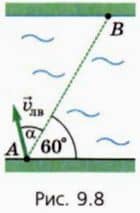а) Скорость лодки относительно воды в 2 раза больше скорости течения. Под каким углом α к линии АВ должна быть направлена скорость лодки относительно воды? б) При какой минимальной скорости лодки относительно воды она сможет попасть в точку В, если скорость течения равна 1 к/с?
Под каким углом к линии АВ надо в этом случае направить киль лодки?
(1 votes, average: 5,00 out of 5)