Свободное падение тел
Падение тел — один из самых часто наблюдаемых видов движения. Изучать падение тел люди начали очень давно. Роняя на землю различные предметы, они установили, что отпущенные без начальной скорости предметы падают вертикально вниз. (Напомним, что вертикалью называют линию отвеса, неподвижного относительно Земли.)
На основании этого был сделан вывод: такое движение является прямолинейным. Сложнее было установить закон движения падающего тела.
Дело в том, что воздух мешает телам падать, оказывая сопротивление их движению. Это подтверждают
Чтобы понять, как зависит сопротивление воздуха от массы и формы падающих тел, проведем ряд экспериментов.
Вначале уроним с одинаковой высоты пустой пакет из-под молока и такой же пустой пакет, смятый в малый комок. Легко убедиться, что смятый в комок пакет упадет на Землю быстрее. Из этого сделаем первый вывод: при падении двух тел с одинаковыми массами окружающий воздух оказывает меньшее сопротивление тому телу, у которого размеры меньше.
Теперь сравним падение одинаковых по форме тел, одно из которых тяжелее другого. Возьмем две одинаковые пластиковые бутылки, одну из которых заполним водой, а другую оставим пустой. Закроем бутылки крышками и сравним их падение с одинаковой высоты. Бутылка с водой упадет быстрее пустой бутылки.
Таким образом, мы приходим ко второму выводу: при одинаковой формы тел сопротивление воздуха падению для тяжелого тела будет менее заметным.
Проведем третий эксперимент. Во время движения автомобиля выставим ладонь наружу через окно. Мы почувствуем, что чем больше скорость автомобиля, тем сильнее будет давить на ладонь встречный воздух.
Это позволяет сделать третий вывод: сопротивление воздуха движению тела увеличивается с увеличением скорости движения.
В этом параграфе мы будем рассматривать падение только таких тел, для которых сопротивлением воздуха можно пренебречь. Чтобы это можно было делать, должны соблюдаться следующие условия: 1) тела должны иметь достаточно малые размеры;
2) тела должны быть достаточно тяжелыми; 3) тела должны падать с небольшой высоты (меньше 100 м), чтобы не успеть разогнаться до больших скоростей, при которых велико сопротивление воздуха движению.
При описании падения таких тел пренебрегают сопротивлением воздуха и считают падение свободным. (Строгое определение свободного падения будет дано позднее, в главе «Силы в механике».)
Многочисленные эксперименты показывают, что свободно падающие тела движутся с ускорением, направленным вертикально вниз. Для этого ускорения принято использовать специальное обозначение g («же»). Модуль ускорения свободного падения вблизи поверхности Земли примерно равен g ≈ 9,81 м/с2 и несколько изменяется в зависимости от географического положения места падения тела. Однако для тех задач, которые мы с вами пока будем решать, эта зависимость несущественна.
Поэтому будем считать, что модуль ускорения свободного падения одинаков во всех точках над поверхностью Земли и равен 10 м/с2.
Таким образом, свободное падение по вертикали является прямолинейным равноускоренным движением.
Свободно падающие тела движутся с ускорением, направленным вертикально вниз.
Мы уже освоили решение задач на прямолинейное равноускоренное движение. Поэтому воспользуемся нашими знаниями и закрепим их на конкретных примерах. Разделим все задачи о свободном падении на два типа:
1) задачи, в которых направления движения тела и ускорения свободного падения совпадают (эти задачи назовем «падение» ); 2) задачи, в которых направления движения тела и ускорения свободного падения противоположны (эти задачи назовем «подъем»).
Ускорение свободного падения всегда направлено вертикально вниз. Поэтому если тело меняет направление своего движения, то рассматриваемый промежуток времени нужно разделить на интервалы так, чтобы на каждом из них тело двигалось только в одном направлении.
Задача «Падение»
С крыши дома высотой h = 45 м срывается и летит вниз сосулька. Определите: а) время падения сосульки; б) скорость сосульки в момент приземления.
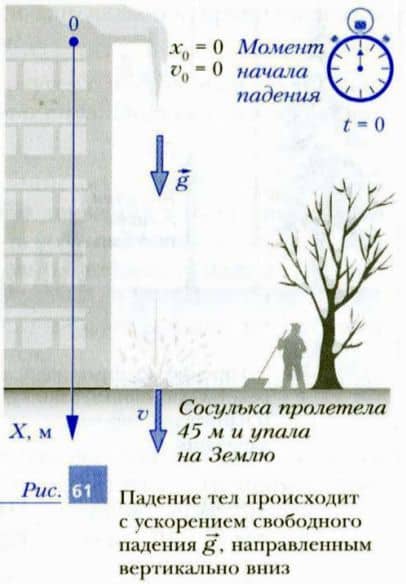
Шаг 1. Выберем систему отсчета так, как показано на рис. 61.
Шаг 2. Начальная координата сосульки x0 = 0.
Шаг 3. Начальная скорость сосульки v0 = 0.
Так как ускорение свободного падения направлено вниз, т. е. в положительном направлении оси X, то его значение будет положительным. В соответствии со сказанным ранее будем считать a = g = 10 м/с2.
Шаг 4. Зависимость координаты сосульки от времени имеет вид:
X = x0 + v0 — t + (a — t2) / 2 = 0 + 0 — t + (g — t2) / 2 = (g — t2) / 2 = (10 — t2) / 2 = 5 — t2.
Шаг 4*. Значение скорости сосульки изменяется со временем:
V = v0 + g — t = 0 + 10 — t = 10 — t.
Видно, что значение скорости падающей сосульки положительно и за каждую секунду увеличивается на 10 м/с. Таким образом, когда тело падает, оно разгоняется.
Шаг 5. Условие окончания падения имеет вид:
X = h = 45 м.
Это означает, что в момент падения t координата сосульки будет равна x = h = 45 (м). Сосулька, пролетев вдоль стены дома расстояние, равное его высоте, окажется на Земле.
Шаг 6. Запишем вместе полученные уравнения, присвоив каждому номер и название:
X = 5 — t2, (1) (закон движения сосульки) v = 10 — t, (2) (зависимость скорости от времени) x = 45. (3) (условие окончания падения)
Шаг 7. Решение уравнений. Чтобы определить время падения сосульки, подставим в условие окончания падения (3) зависимость координаты тела от времени из уравнения (1):
5 — t2 = 45, t2 = 9, t = 3 с.
Таким образом, сосулька окажется на Земле через время t = 3 с после начала падения. Для нахождения скорости сосульки в момент удара о Землю подставим найденное время в зависимость скорости от времени (2):
V = 10 — 3 = 30 (м/с).
Значит, сосулька подлетает к Земле со скоростью, имеющей значение v = 30 м/с.
Значение скорости получилось положительным. Следовательно, скорость направлена в положительном направлении оси X, т. е. вертикально вниз.
Задача «Подъем»
Праздничная новогодняя ракета в результате мгновенного сгорания ее порохового заряда начинает подниматься (взлетать) с Земли вертикально с начальной скоростью, имеющей значение v0 = 50 м/с. Определите максимальную высоту подъема ракеты.

Шаг 1. Выберем ось X так, как показано на рис. 62. Часы (секундомер) включим в момент старта.
Шаг 2. Начальная координата ракеты x0 = 0.
Шаг 3. Значение начальной скорости ракеты v0 = 50 м/с.
Шаг 4. Зависимость координаты ракеты от времени имеет вид:
X = x0 + v0 — t + (a — t2) / 2 = x0 + v0 — t — (g — t2) / 2 = 0 + 50 — t — (10 — t2) / 2.
Внимание! Направление вектора ускорения свободного падения противоположно положительному направлению оси X. Поэтому значение ускорения тела отрицательно (тело тормозится).
Шаг 4*. Значение скорости ракеты изменяется со временем:
V = v0 + a — t = v0 — g — t = 50 — 10 — t.
Значение начальной скорости ракеты положительно, т. е. скорость направлена вверх. При этом значение скорости уменьшается со временем — с каждой секундой она становится меньше на 10 м/с. Иначе говоря, когда тело поднимается вверх, оно тормозится.
Шаг 5. В самой верхней точке подъема скорость ракеты становится равной нулю. Поэтому условие окончания «подъема» имеет вид: v = 0.
После этого ракета начинает падать (с этого момента начинается задача «падение»).
Шаг 6. Объединим полученные уравнения, присвоив каждому номер и название:
X = 50 — t — 5 — t2, (1) (закон движения ракеты) v = 50 — 10 — t, (2) (зависимость скорости от времени) v = 0. (3) (условие окончания подъема)
Шаг 7. Решение уравнений. Определить из уравнения (1) высоту, на которую поднялась ракета, мы не можем, так как неизвестно время подъема. Его мы можем найти из уравнений (2) и (3).
Для этого подставим в условие окончания подъема (3) зависимость скорости от времени (2). Получим:
50 — 10 — t = 0, 10 — t = 50, t = 5 с.
Таким образом, ракета поднималась в течение t = 5 с. Теперь найдем ее координату в момент времени t = 5 с (т. е. максимальную высоту подъема). Для этого подставим найденное время подъема в закон движения (1):
X = 50 — 5 — 5 — 52 = 125 (м).
Ответ: ракета поднялась на высоту 125 м.
Отметим, что ускорение поднимающейся вверх ракеты постоянно, направлено вниз и по модулю равно |g| = 10 м/с2. Таким образом, движение происходит с ускорением свободного падения. Поэтому такое движение тела начиная с момента старта также является свободным падением.
Итоги
Свободное падение по вертикали является прямолинейным равноускоренным движением.
Свободно падающие тела движутся с постоянным ускорением g, направленным вертикально вниз. Модуль этого ускорения |g| ≈ 9,8 м/с2 ≈ 10 м/с2.
Если положительное направление оси X выбрать так, чтобы оно совпадало с направлением движения тела, то все задачи о свободном падении тел вдоль вертикали (так же как и задачи о любом равноускоренном прямолинейном движении) можно свести к задачам двух типов: 1) задача «падение». В этом случае g > 0 и значение скорости тела со временем увеличивается;
2) задача «подъем». В этом случае g < 0 и значение скорости тела со временем уменьшается.
Задачу, в которой поднимающееся вертикально вверх тело, достигнув верхней точки, затем начинает падать (например, брошенный вверх камень), следует разбить на две задачи: 1) «подъем» до верхней точки; 2) «падение» из верхней точки.
Вопросы
Имеются два тела одинаковых формы и размеров, но первое существенно легче второго. Какое из этих двух тел раньше упадет, если они начинают падать с нулевой начальной скоростью с одной и той же высоты? Почему? Какие условия должны выполняться, чтобы движение тела можно было считать свободным падением? Как скорость свободно падающего тела изменяется со временем? Куда направлено ускорение свободно падающего тела? Куда может быть направлен вектор скорости при вертикальном свободном падении? Что общего между задачей «падение» и задачей «разгон» из предыдущего параграфа? Что общего между задачей «подъем» и задачей «торможение» из предыдущего параграфа?
Упражнения
1. Изучите выводы о влиянии воздуха на падающие тела. Предложите свои эксперименты для проверки справедливости этих выводов. Сформулируйте цель каждого эксперимента.
Обсудите эти эксперименты в классе, проведите их.
2. Заполните таблицу для падающей сосульки из задачи 1 («падение»). Как изменяются со временем: а) значение скорости; б) координата сосульки? 
3. Упавший с крыши дома камень летит к Земле в течение времени t = 4 с. Определите: а) высоту дома; б) скорость подлета камня к Земле.
4. Заполните таблицу для поднимающейся вертикально вверх ракеты из задачи 2 («подъем»). Как изменяются со временем: а) значение скорости; б) координата ракеты? 
5. На рис. 63 и 64 приведены графики зависимостей значения скорости от времени для задач «падение» сосульки и «подъем» ракеты. Объясните с помощью графиков, как изменялись скорости этих тел в процессе движения. 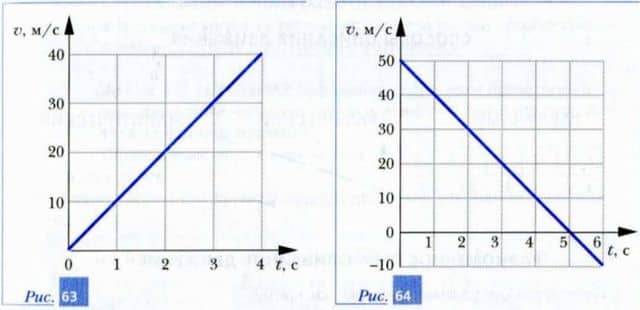
6. Запланируйте и проведите эксперимент с целью подтвердить гипотезу о прямолинейности свободного падения тел из состояния покоя относительно Земли. Используйте отвес. Сформулируйте, каким условиям должны удовлетворять тела, чтобы их движение можно было считать свободным падением.
7. Решите задачу «подъем» в общем виде. Получите выражения для времени подъема и его высоты. Представьте их в виде: t = v0/g, h = v02 / (2 — g).
Проведите анализ полученных результатов.
8. Решите задачу «падение» в общем виде. Получите выражения для времени падения и конечной скорости. Представьте их в виде: t2 = (2 — h) / g, v2 = 2 — g — h.
Проведите анализ полученных результатов.
