Взаимодействие тел. Третий закон Ньютона
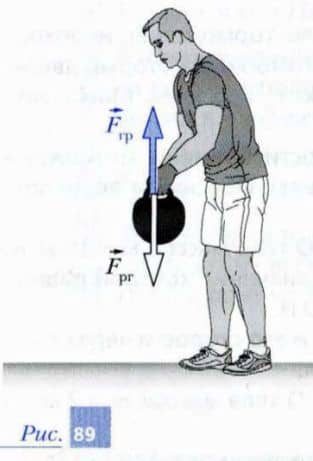
Представьте себе, что вы поднимаете гирю, действуя на нее рукой с некоторой силой Fгр, направленной вверх (рис. 89). В этом случае вы почувствуете, что гиря тоже действует на вашу руку.
При этом гиря будет тянуть вашу руку вниз с силой Fрг.
Индексы «г» (гиря) и «р» (рука) в записи Fгр означают, что эта сила действует на гирю (первый индекс) со стороны руки (второй индекс). Соответственно индексы «р» и «г» в записи силы Fрг означают, что эта сила действует на руку (первый индекс) со стороны гири (второй индекс). Такую систему обозначения
Оказывается, силы в природе всегда возникают парами. Если первое тело действует на второе, то второе тело действует на первое. Таким образом, действие двух тел друг на друга всегда имеет взаимный характер.
При этом говорят, что два тела взаимодействуют друг с другом. Отметим, что силы взаимодействия приложены к разным телам.
Эти силы подчиняются конкретным правилам, которые Ньютон сформулировал в виде фундаментального закона природы. В настоящее время этот закон называют третьим законом Ньютона.
Два тела взаимодействуют друг с другом с силами: 1) равными по модулю; 2) противоположными по направлению;
3) лежащими на одной прямой.
Строго говоря, в третьем законе Ньютона также сказано, что силы взаимодействия двух тел всегда являются силами одной природы. Но об этом мы поговорим с вами позднее, когда изучим виды существующих в природе сих.
Подчеркнем еще раз, что силы, о которых говорится в третьем законе Ньютона, приложены к равным телам, т. е. к телам, которые взаимодействуют друг с другом. Поэтому эти силы не могут уравновесить друг друга.
Силы взаимодействия двух тел приложены к разным телам и поэтому не уравновешивают друг друга.
Обратим внимание на то, что, в отличие от второго закона Ньютона, в котором речь идет об одном теле, в третьем законе речь идет о двух взаимодействующих друг с другом телах.
Применим третий закон Ньютона к силам, изображенным на рис. 89.
В соответствии с первым пунктом |Fрг| = |Fгр|. То есть модуль силы, с которой на руку действует гиря, равен модулю силы, с которой на гирю действует рука.
В соответствии со вторым пунктом Fгр = — Fрг. Действительно, сила Fгр, с которой рука действует на гирю, направлена вверх, а сила Fрг, с которой гиря действует на руку, направлена в противоположную сторону — вниз.
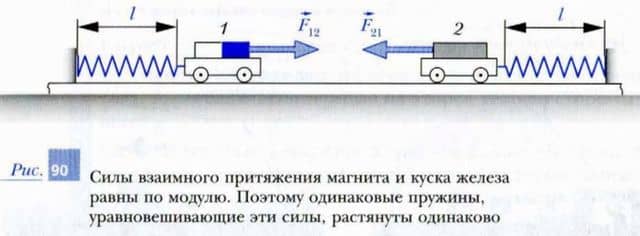
Как вы уже знаете, два тела могут взаимодействовать друг с другом не только при касании, но и на расстоянии. Например, кусок железа и магнит (рис. 90), расположенные на разных тележках, притягиваются друг к другу.
При этом силы их взаимодействия удовлетворяют третьему закону Ньютона: они равны по модулю, противоположны по направлению и лежат на одной прямой.
Со временем мы убедимся в том, что с помощью второго и третьего законов Ньютона можно вывести большинство законов механики и решать практически все механические задачи. Уже в следующей главе, посвященной видам сил в механике, вы увидите, насколько эффективно использование законов Ньютона.
Поясним, как надо использовать законы Ньютона при решении задач, на следующем простом примере.
На рис. 91 изображен локомотив, толкающий перед собой вагон массой m = 40 т по горизонтальному участку железнодорожного пути. В результате действия локомотива вагон движется по рельсам с ускорением, модуль которого |a| = 1 м/с2.
Найдем силу Fлв, действующую на локомотив со стороны вагона, считая, что в горизонтальном направлении других действий на вагон нет.

Решение. Выберем систему отсчета, связанную с рельсами: направим ось X по ходу движения локомотива. Поскольку рельсы неподвижны относительно Земли, связанную с ними систему отсчета можно считать инерциальной. Будем считать вагон и локомотив точечными телами.
Направление ускорения вагона совпадает с положительным направлением оси X. Поэтому значение a этого ускорения положительно, а значение Fвл силы, действующей на вагон со стороны локомотива, согласно второму закону Ньютона удовлетворяет соотношению m — a = Fвл. Следовательно,
Fвл = m — a = 40000 кг — 1 м/с2 = 40 кН.
Теперь можно определить силу Fлв, действующую на локомотив со стороны вагона. Согласно третьему закону Ньютона модуль этой силы равен найденному нами значению Fвл. Направлена же сила Fлв противоположно силе Fвл, т. е. противоположно направлению ускорения a вагона.
Итоги Если первое тело действует на второе, то второе тело при этом действует на первое. Про такие тела говорят, что они взаимодействуют друг с другом.
Третий закон Ньютона. Два тела взаимодействуют друг с другом с силами: 1) равными по модулю;
2) противоположными по направлению; 3) лежащими на одной прямой.
Кратко этот закон может быть записан в виде: F12 = — F21, где F12 — сила, действующая на первое тело со стороны второго тела, F21 — сила, действующая на второе тело со стороны первого.
Силы, о которых говорится в третьем законе Ньютона, приложены к разным телам, т. е. к телам, которые взаимодействуют друг с другом. Поэтому эти силы не могут уравновешивать друг друга.
Вопросы
Приведите примеры взаимодействующих тел. Сформулируйте третий закон Ньютона. Какими свойствами обладают силы взаимодействия? Могут ли силы взаимодействия уравновесить друг друга? Чему равна сумма сил взаимодействия двух тел?
Упражнения
Определите силу (модуль и направление), с которой давит на спинку сиденья водитель массой m = 80 кг, если его автомобиль разгоняется по прямолинейному горизонтальному участку дороги с ускорением a = 4 м/с2. Считайте, что в горизонтальном направлении на водителя действует только спинка сиденья. Определите, с какой силой действует на ремень безопасности водитель массой m = 100 кг, если после нажатия на педаль тормоза его автомобиль сбрасывает скорость от 108 км/ч до нуля за 6 с на прямолинейном горизонтальном участке дороги. Считайте, что в горизонтальном направлении на водителя действует только ремень безопасности.
