Зависимость силы упругости от деформации. Закон Гука
Зависимость сил упругости от деформации была установлена экспериментально английским физиком Робертом Гуком в середине XVII в. Давайте и мы обратимся к опыту.
Подвесим к потолку легкий резиновый шнур длиной l0 (рис. 99, а). К нижнему концу шнура прикрепим груз небольшой массы m. Начнем постепенно отпускать груз, чтобы он медленно двигался вниз, а шнур все больше и больше растягивался.
Когда мы перестанем удерживать груз, длина шнура станет равной l1, а груз будет висеть неподвижно в системе отсчета, связанной с Землей (рис. 99, б). Величина Δl1
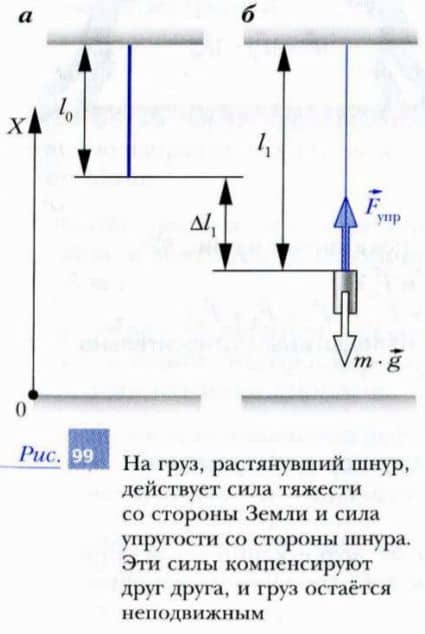
Определим силу, с которой тело массой m действует на шнур. Для этого воспользуемся известными нам законами Ньютона. Так как ускорение груза равно нулю, то согласно второму закону Ньютона сумма всех сил, действующих на груз, равна нулю.
Иначе говоря, силы, действующие на груз, скомпенсировали (уравновесили) друг друга. Выясним, какие это силы. Во-первых, как мы уже знаем, на груз действует сила тяжести, равная по модулю m — g и направленная вертикально вниз в отрицательном направлении оси X. Во-вторых, на груз действует сила упругости растянутого шнура.
Именно эта сиаа компенсирует (уравновешивает) действие силы тяжести. Запишем второй закон Ньютона для груза с учетом того, что его ускорение равно нулю, а сила тяжести направлена в отрицательном направлении оси X:
0 = Fупр — m — g.
Следовательно, значение силы упругости Fупр = m — g, т. е. положительно. Поэтому сила упругости шнура, действующая на груз, направлена в положительном направлении оси X — вертикально вверх. При этом нижний конец деформированного шнура сместился в отрицательном направлении оси X — вниз.
Таким образом, сила упругости шнура направлена в сторону, противоположную вызвавшему ее смещению. Иначе говоря, шнур стремится вернуться в исходное, нерастянутое состояние.
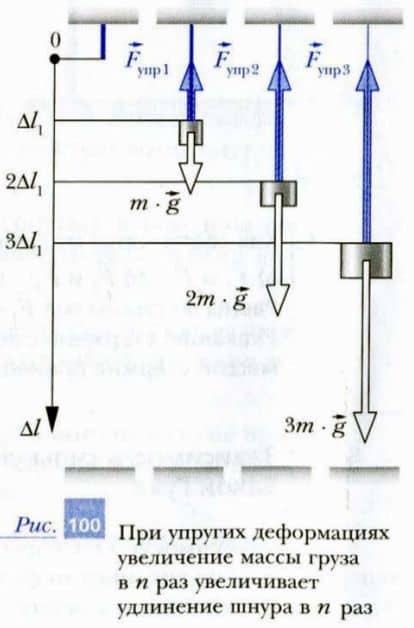
Снимем висящий груз. Если деформация шнура была упругой, то длина шнура станет первоначальной. Аккуратно подвесим на шнур груз массой 2m.
Измерим длину растянутого шнура l2. Если шнур деформировался упруго, то удлинение шнура Δl2 = l2 — l0 под действием силы 2m — g будет равно 2Δl1 (рис. 100). Продолжая увеличивать массы подвешиваемых грузов, можно прийти к следующему выводу: при упругих деформациях шнура увеличение в n раз массы подвешиваемого груза приводит к увеличению удлинения шнура также в n раз.
Следовательно, удлинение шнура при упругих деформациях пропорционально модулю силы упругости.
При упругих деформациях отношение модуля силы упругости |Fупр| к удлинению шнура Δl является постоянным. Это отношение характеризует упругие свойства деформируемого тела и называется коэффициентом жесткости (жесткостью) этого тела.
Обычно коэффициент жесткости обозначают латинской буквой k. Так как перемещение Δl незакрепленного конца шнура направлено в сторону, противоположную силе Fупр этот факт часто записывают в виде:
Fупр = — k — Δl.
Гук опытным путем установил: Для любого тела при упругих деформациях эти деформации прямо пропорциональны вызывающим их силам. F = k — Δl.
Это утверждение называют законом Гука.
Отметим, что в шнуре или нити силы упругости возникают лишь при попытке увеличить их длину (растянуть). В пружинах и стержнях силы упругости возникают не только при их растяжении, но и при сжатии.
При упругих деформациях сжатия и растяжения жесткость тела не изменяется. Поскольку при растяжении длина тела увеличивается, а при сжатии уменьшается, в первом случае удлинение тела считают положительным (Δl > 0), а во втором — отрицательным (Δl 0.
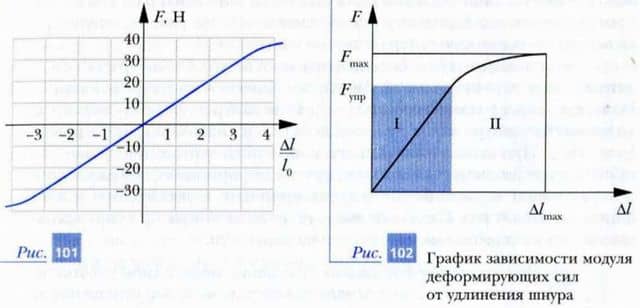
Эксперименты показывают, что для любого тела существует определенное критическое значение модуля деформирующих его сил Fкр, начиная с которого деформации тела перестают быть упругими. То есть после прекращения действия деформирующих сил, модули которых превышали Fкр, размеры (и форма) тела не возвращаются к исходным. В этом случае в теле остаются остаточные деформации.
При действии на тело таких сил его жесткость перестает быть постоянной (возможно даже разрушение тела).
На рис. 102 показан примерный вид графика зависимости модуля деформирующих сил F от удлинения шнура Δl. Обратим внимание на то, что на этом графике выделяются две области. В пределах области I график имеет вид прямой линии, проходящей через начало координат.
Эту область называют областью малых деформаций, или малых деформирующих сил. В этой области выполняется закон Гука. Область II область больших деформаций, или больших деформирующих сил, ограничена точкой (Δlmax, Fmax), в которой происходит разрыв шнура.
В этой области зависимость силы упругости от величины деформаций не является линейной.
В области I деформации шнура являются упругими, в области II — пластическими.
Итоги
Закон Гука. Для любого тела при упругих деформациях эти деформации прямо пропорциональны вызывающим их силам. F = k — Δl, где k — коэффициент жесткости (жесткость) тела.
Вопросы
В каких случаях возникают силы упругости? Куда направлены эти силы при деформациях сжатия и растяжения? Зарисуйте примеры таких деформаций и укажите на рисунках направления действующих сил упругости. Как соотносятся силы упругости и силы, вызывающие деформации? Что такое жесткость тела? При каких деформациях жесткость тела не изменяется? Приведите примеры тел различной жесткости.
Упражнения
1. Определите жесткость пружины при упругих деформациях, используя рис. 101. Считайте длину недеформированной пружины l0 = 1 см.
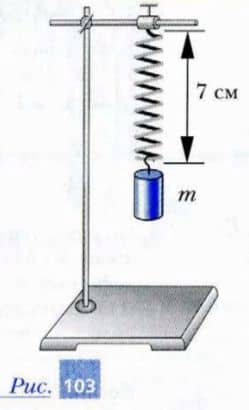
2. Определите массу груза на пружине, прикрепленной к неподвижному штативу (рис. 103). Жесткость пружины k = 3 Н/см.
Длина недеформированной пружины l0 = 5 см.
3. Каково соотношение между силами упругости, действующими на руку и стол со стороны сжатой пружины (см. рис. 96), если пружина в сжатом состоянии покоится относительно Земли? Рассмотрите два случая: а) пружина легкая; б) пружина тяжелая.
