Применение условий равновесия твердого тела
Рассмотрим примеры того, как можно на практике применить условия равновесия твердого тела.
Пример 1. Равноплечие весы
Еще с древнейших времен для определения массы тел люди использовали равноплечие весы (рис. 137). Понять принцип их работы просто, если воспользоваться вторым условием равновесия твердого тела.
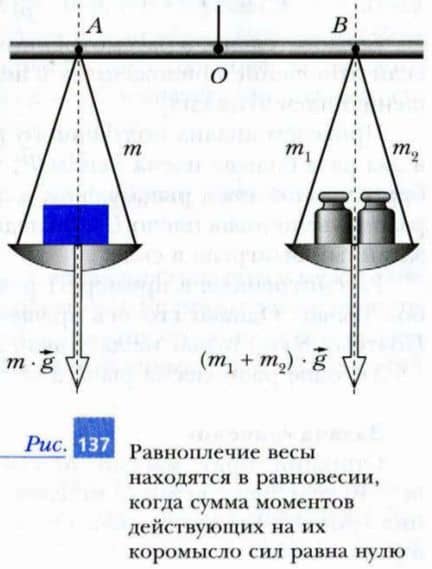
Коромысло весов может поворачиваться вокруг оси, проходящей через точку O. На равных расстояниях от оси вращения
M — g — OA — (m1 + m2) — g — OB = 0
Так как плечо OA силы тяжести груза равно плечу OB силы тяжести гирь, то уравнение обратится в тождество при условии, что m = m1 + m2. Таким образом, равноплечие весы будут находиться в равновесии, если суммарная масса гирь будет равна массе взвешиваемого груза.
Если массы груза и гирь не равны друг другу, то коромысло весов начнет разворачиваться в сторону большего по модулю момента силы тяжести (в сторону большей массы). Чашка весов с большей массой начнет опускаться. Добавляя (или уменьшая) число гирь известной массы, можно достичь равновесия и таким образом измерить неизвестную массу груза.
Пример 2. Рычаг
Рычагом называют твердое тело, способное вращаться вокруг неподвижной оси (или опоры). Применение рычага позволяет получить выигрыш в силе — преодолеть действие большей силы, приложив меньшую силу. Каким образом это можно сделать?
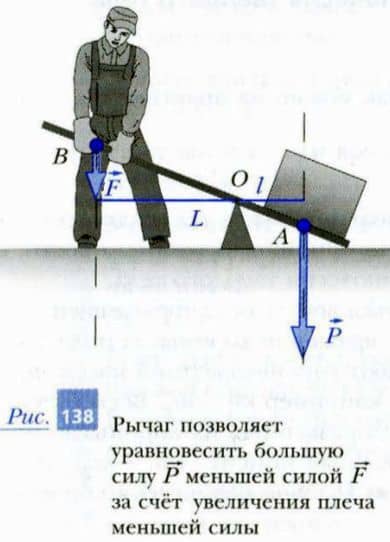
Рассмотрим человека, поднимающего камень весом P с помощью рычага (рис. 138). Человек действует на противоположный конец рычага силой F, направленной вертикально вниз. Под действием моментов сил F и P рычаг может вращаться вокруг оси O. Обозначим плечо силы F символом L, а плечо силы P — символом l. Рычаг будет находиться в равновесии, если сумма вращающих его моментов сил будет равна нулю:
F — L — P — l = 0 или F/P = l/L
Следовательно, в рассмотренном случае рычаг находится в равновесии, если отношение приложенных к нему сил обратно пропорционально отношению плеч этих сил.
Проведем анализ полученного результата. Если плечо L силы F будет в два раза больше плеча l силы P, то для поднятия камня человек должен будет приложить к рычагу силу, в два раза меньшую веса камня. Таким образом, увеличивая плечо L прикладываемой силы, можно получить заранее заданный выигрыш в силе.
Рассмотренные в примере 1 равноплечие весы также представляют собой рычаг. Однако его ось вращения совпадает с серединой коромысла. Поэтому такой рычаг не дает выигрыша в силе.
Условие равновесия рычага можно использовать для решения задач.
Задача «качели»
Старший брат массой M = 60 кг посадил младшего брата массой m = 40 кг на легкую доску качелей на расстоянии L = 3 м от оси ее вращения (рис. 139). Куда должен сесть старший брат, чтобы доска находилась в равновесии?
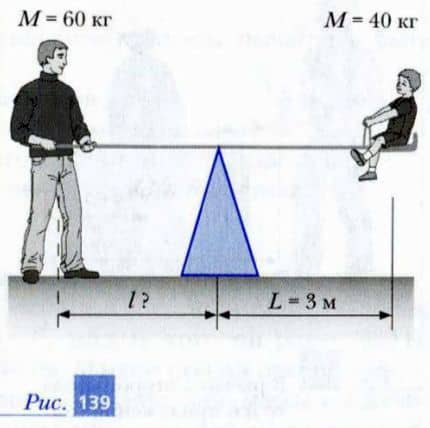Решение. Ясно, что старший брат должен сесть с противоположной стороны на таком расстоянии l от оси вращения, чтобы выполнялось условие равновесия доски качелей относительно этой оси: M — g — l — m — g — L = 0.
Следовательно,
L = (m — L) / M = (40 кг — 3 м) / 60 кг = 2 м.
Ответ: чтобы качели находились в равновесии, старший брат должен сесть на расстоянии 2 м от оси вращения качелей.
Найдите силу, с которой доска качелей при этом будет действовать на ось вращения (опору). Массой доски качелей можно пренебречь.
Решение. По третьему закону Ньютона искомая сила F, с которой доска качелей действует на ось вращения (опору), равна по модулю силе N реакции опоры, с которой ось вращения действует на доску. Для того чтобы найти силу N реакции опоры, применим к доске первое условие равновесия твердого тела.
На доску действуют три силы (со стороны двух братьев и со стороны оси вращения). Если ось системы отсчета, связанной с Землей, направить вертикально вверх, то первое условие равновесия твердого тела для доски примет вид: N — M — g — m — g = 0. Следовательно, искомая сила направлена вертикально вниз, а ее модуль равен
F = N = (M + m) — g = 1000 Н = 1 кН.
Ответ: модуль силы, с которой доска качелей действует на опору, равен 1 кН.
Мы рассмотрели рычаги, в которых ось вращения находится между точками приложения действующих сил. На практике используют также рычаги, у которых точки приложения сил находятся по одну сторону от оси вращения. Такие рычаги часто называют рычагами второго рода. На рис.
140 изображен подобный рычаг.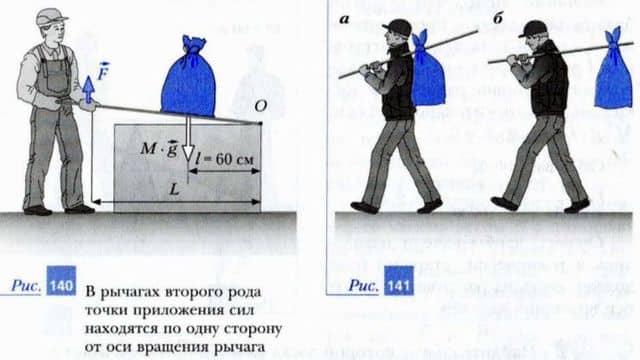 
Задача «рычаг второго рода»
На каком расстоянии L от точки опоры O (см. рис. 140) должен взяться за легкий рычаг рабочий, чтобы приподнять груз массой M = 200 кг? Линия действия веса этого груза проходит на расстоянии l = 60 см от точки опоры. Рабочий прикладывает к рычагу силу, направленную вертикально вверх, ее модуль F = 600 Н.
Решение. На рычаг действуют вес груза P = M — g и сила F со стороны рабочего. При этом относительно оси вращения (точки опоры O) момент веса груза положителен, а момент силы, приложенной рабочим, отрицателен. Поэтому условие равновесия данного рычага имеет вид:
M — g — l — F — L = 0.
Следовательно, L = (M — g — l) / F = (200 кг -10 м/с2 — 0,6 м) / 600 Н = 2 м.
Ответ: рабочий должен взяться за рычаг на расстоянии L = 2 м от точки опоры.
Итоги
Рычагом называют твердое тело, способное вращаться вокруг неподвижной оси (или опоры).
Рычаг дает выигрыш в силе, равный отношению плеч сил. При этом отношение модулей приложенных к нему сил обратно пропорционально отношению плеч этих сил.
Вопросы
Что называют рычагом? Приведите примеры рычагов в быту и в технике. Сформулируйте условие равновесия рычага. Как с помощью рычага получить выигрыш в силе? Чем отличается рычаг первого рода от рычага второго рода? Предложите способы определения равноплечности весов.
Упражнения
Определите массу камня, который приподнимает человек (рис. 138), прикладывая силу F, модуль которой равен 800 Н. Расстояние OB = 3 м, OA = 40 см. Массой рычага пренебречь. Соберите группу из пяти человек. Узнайте свои массы и рассчитайте расстояния от точки опоры доски качелей, на которые каждому из вас необходимо сесть, чтобы качели с пятью учащимися находились в равновесии (сделайте рисунок, на котором изобразите действующие на доску силы и их плечи). Для проверки полученного ответа проведите эксперимент с качелями (используйте рулетку). Как с помощью неравноплечих весов и набора гирь определить неизвестную массу груза? В каком случае палка сильнее давит на плечо путника, показанного на рис. 141, а и б? (Подсказка: определите, рычагом какого рода является палка.) Допустим, вам нужно поднять груз массой 100 кг, а вы можете приложить в вертикальном направлении силу не более 200 Н. Какой рычаг второго рода потребуется вам для выполнения задачи? Нарисуйте схему эксперимента, указав на ней силы и их плечи.
(1 votes, average: 5,00 out of 5)