Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний
Цель урока: получить основное уравнение, описывающее свободные электрические колебания в контуре; вывести формулу, с помощью которой можно вычислить период свободных электрических колебаний.
Ход урока
Проверка домашнего задания методом индивидуального опроса и решения задач
1. Как происходят превращения энергии в колебательном контуре?
2. Провести аналогию между электромагнитными и механическими колебаниями (по плакату)
3. Задача №1 из упр. 4.
Дано : q=10-5Кл; С=1·10-8; Q — ? Q = W = q2/2C = 10-5/2·10-8= 0,5
4. Задача №2 из упр. 4
Дано: L =0,003 Гн, С = 13,4·10-12Ф; Т — ? Т = 2π QUOTE 
= 6,28 QUOTE 
=0,2·10-6c.
5. Контур состоит из конденсатора и активного сопротивления. Возникнут ли в такой системе свободные колебания.
Изучение нового материала
Рассмотрим количественную теорию процессов в колебательном контуре. Будем считать ,
что сопротивление всего контура R = 0. С помощью закона сохранения энергии получим уравнение, которое описывает свободные электрические колебания в контуре. Запишем уравнение: W = L i2/2 + q2/2C — эта энергия не меняется со временем, так как R=0. Производная полной энергии = 0, так как энергия постоянна.
( QUOTE 
)′ +( QUOTE 
)′ = 0 или (L i2/2)′ = — (q2/2C)′ — скорость изменения энергии магнитного поля равна скорости изменения энергии электрического поля. На то, что энергия магнитного поля убывает, а электрического – возрастает (и наоборот) показывает знак «минус»
Решим производные: L 2 I i′/2 = — 2 q q′/2C; I = lim QUOTE 
= q′; L i′I = — qi/C;
q′′ = — q/ LC – основное уравнение описывающее свободные колебания в контуре. (Оно аналогично x′′= — k x/m – для механических колебаний)
Формула Томсона.
Коэффициент 1/LC — квадрат циклической частоты для электромагнитных колебаний; так как k/m- квадрат собственной частоты для механических колебаний.
ω0 = 1/LC; Период свободных колебаний определится по формуле:
Т= 2π/ ω0 = 2π QUOTE – формула Томсона
С увеличением емкости и индуктивности увеличивается период свободных колебаний. Так как с увеличением индуктивности ток медленнее возрастает в единицу времени и медленнее уменьшается до нуля. Время для перезарядки конденсатора требуется больше, чем больше его емкость.
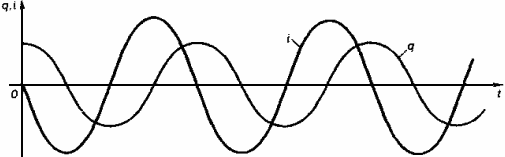
Гармонические колебания тока и заряда.
Колебания силы тока опережают колебания заряда по фазе на π/2.
x = xm QUOTE 
— изменение координаты по гармоническому закону.
Запишем по аналогии уравнение для меняющегося заряда конденсатора: = q = qm QUOTE 
Сила тока также изменяется по гармоническому закону:
I = q′ = — ω QUOTE 
qm QUOTE 
= Im QUOTE 
Величина Im= qmω₀ -амплитуда колебаний силы тока.
Из – за потерь энергии эти колебания будут затухающими. Период колебания будет тем больше, чем больше сопротивление системы.
Закрепление изученной темы.
1 Пояснить разницу между вынужденными и свободными электрическими колебаниями.
2. Если увеличить емкость конденсатора в 2 раза, как изменится период свободных колебаний? (увеличится в 2 раза).
3. Конденсатор разряжается через катушку, как будут изменяться амплитуды колебаний тока и заряда?
Подведем итоги урока
Домашнее задание: § 30, упр. 4 № 3.
(1 votes, average: 5,00 out of 5)