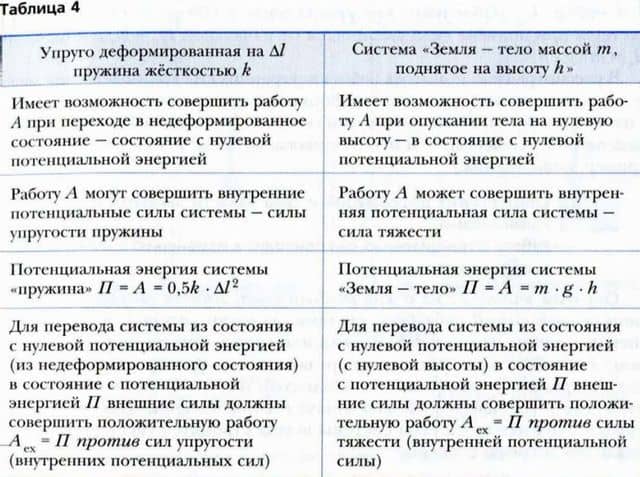
Система тел. Потенциальная энергия
Не только кинетическая энергия определяет величину работы, которую могут совершить тела системы. Действительно, между телами обычно существуют силы взаимодействия. Пусть имеются несколько взаимодействующих друг с другом тел. Будем рассматривать эти тела как нечто целое.
В таких случаях говорят, что эти тела образуют систему тел.
Все силы, действующие на тела системы, принято разделять на два вида.
Силы взаимодействия между телами, принадлежащими системе тел, называют внутренними силами.
Силы, действующие на принадлежащие
Внешние силы принято обозначать индексом «ex» (от англ. external — «внешний»).
Поясним сказанное на примере. Представим резиновый шнур, который растягивают в противоположные стороны два мальчика (рис. 127). Такой шнур можно рассматривать как систему тел, состоящую из частей шнура.
При этом силы взаимодействия частей шнура друг с другом (силы упругости) будут внутренними силами. Эти силы изображены на рисунке голубыми стрелками. Напротив, силы, приложенные мальчиками к концам шнура, будут внешними силами, так как мальчики не входят в выбранную систему тел.
Эти силы изображены на рисунке контурными стрелками.
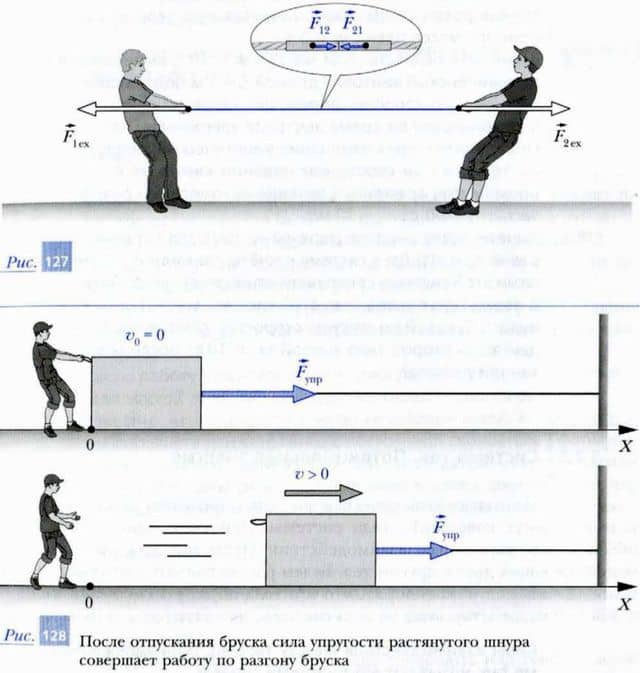
Частички растянутого резинового шнура, взаимодействуя силами упругости, притягиваются друг к другу. Эти силы стремятся вернуть шнур (систему тел) в недеформированное состояние. На рис. 128 изображен растянутый шнур, который также удерживают в деформированном состоянии.
При этом части шнура (тела системы) взаимодействуют друг с другом силами упругости (внутренними силами). Наоборот, части сжатой пружины (рис. 129), которую удерживают в деформированном состоянии, отталкиваются друг от друга силами упругости (внутренними силами).
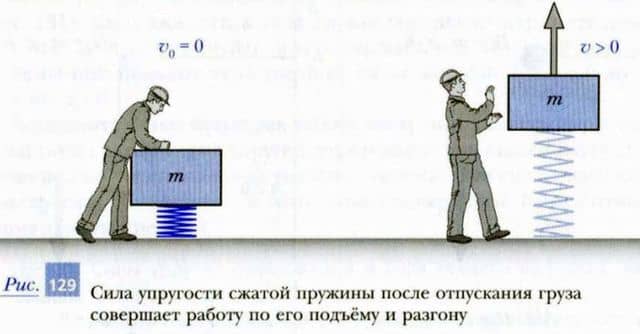
Если перестать удерживать шнур и пружину в деформированном состоянии, они перейдут в исходное состояние (см. рис. 128 и 129). При этом силы упругости совершат определенную работу.
Таким образом, в рассмотренных системах тел действуют внутренние силы, способные совершить работу только за счет изменения взаимного расположения тел. В этом случае говорят, что система обладает потенциальной энергией (от лат. potentia — «возможность»).
Потенциальная энергия — та часть энергии системы тел, которая определяется взаимным расположением входящих в систему тел или их частей и силами взаимодействия между ними.
Потенциальную энергию системы будем обозначать буквой П.
Потенциальную энергию так же, как работу и кинетическую энергию, в СИ измеряют в джоулях.
Например, деформированная пружина обладает потенциальной энергией. Эта энергия равна работе, которую могут совершить силы упругости при возвращении пружины в недеформированное состояние. Потенциальную энергию недеформированной пружины считают равной нулю.
Пружина жесткостью k, упруго растянутая (или сжатая) на величину Δl, обладает потенциальной энергией П = 0,5k — Δl2. Эту формулу мы выведем позднее.
Потенциальной энергией обладает и система «тело — Земля». Как вы знаете, на любое тело вблизи поверхности Земли действует сила тяжести. При поднятии или опускании тела сила тяжести совершает работу.
Иначе говоря, сила тяжести в системе «тело — Земля» может совершать работу при изменении взаимного расположения тела и Земли.
Рассчитаем потенциальную энергию системы «тело — Земля», считая тело точечным. Условимся, что потенциальная энергия такой системы равна нулю, когда тело находится на поверхности Земли.
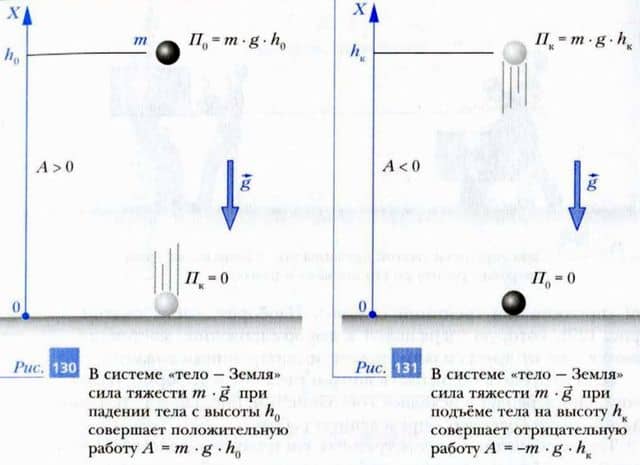
Пусть тело массой m удерживается на высоте h0 от поверхности Земли (рис. 130). Если отпустить тело, то под действием силы тяжести оно устремится к поверхности Земли.
При этом сила тяжести совершает над телом положительную работу, так как направления силы тяжести и движения тела совпадают. К тому моменту, когда тело достигнет поверхности Земли, совершенная силой тяжести работа будет равна A = m — g — h0, где g — модуль ускорения свободного падения. Потенциальная энергия рассматриваемой системы в конечном состоянии Пк, как мы условились, равна нулю.
Следовательно, в начальном состоянии (когда тело находилось на высоте h0) наша система обладала потенциальной энергией П0 = A = m — g — h0.
Таким образом, потенциальная энергия системы «тело — Земля» равна П = m — g — h, если точечное тело массой m находится над поверхностью Земли на высоте h. При этом потенциальную энергию системы «тело — Земля» при h = 0 считают равной нулю.
Пусть теперь тело поднимается с нулевой высоты h0 = 0 на высоту h = hк (рис. 131). Сила тяжести в этом случае совершает отрицательную работу A = — m — g — hк. (Обоснуйте это утверждение!) Потенциальная энергия системы при подъеме тела увеличится от начальной П0 = 0 до конечной Пк = m — g — h.
В рассмотренных примерах работа внутренних сил взаимодействия между частями системы (сил упругих деформаций или силы тяжести) приводит к изменению потенциальной энергии системы. Эти силы называют потенциальными. (Существуют и непотенциальные силы. К ним относятся, например, силы трения.)
Силы упругих деформаций и сила тяжести являются потенциальными силами.
Работа потенциальных сил приводит к изменению потенциальной энергии системы.
Обратим внимание на очень важный факт. Любая система, предоставленная самой себе (т. е. система, на части которой не действуют внешние тела), стремится уменьшить свою потенциальную энергию. Действительно, растянутый резиновый шнур стремится сжаться, сжатая пружина — распрямиться.
Поднятый над поверхностью Земли камень стремится упасть на Землю. Иначе говоря, потенциальные силы взаимодействия между частями системы всегда стремятся уменьшить потенциальную энергию системы.
Чтобы потенциальная энергия системы не изменялась, необходимо, чтобы на части системы действовали другие силы (внешние силы или силы трения), уравновешивающие внутренние потенциальные силы. Например, сжатая (или растянутая) пружина может оставаться в деформированном состоянии, если к ней приложены внешние силы, уравновешивающие силы упругости.
Если внешние силы будут совершать над телами системы положительную работу против потенциальных сил, то потенциальная энергия системы будет увеличиваться. Например, если мы растягиваем резиновый шнур или сжимаем пружину, совершая работу против сил упругости, то потенциальная энергия системы увеличивается.
То же будет происходить, если поднимать рукой камень, совершая работу против силы тяжести. Напротив, если внутренние потенциальные силы совершают положительную работу, то потенциальная энергия системы уменьшается. Так, сжатая пружина (см. рис.
129), разжимаясь, поднимает и разгоняет тело массой m. При этом потенциальная энергия пружины уменьшается.
Сведем результаты нашего рассмотрения в таблицу (табл. 4).
Итоги
Потенциальная энергия — та часть энергии системы тел, которая определяется взаимным расположением входящих в систему тел или их частей и силами взаимодействия между ними.
Потенциальная энергия системы тел равна работе, которую совершают потенциальные силы при переходе системы в состояние с нулевой потенциальной энергией.
Пружина жесткостью k, упруго растянутая (или сжатая) на величину Δl, обладает потенциальной энергией П = 0,5k — Δl2.
Потенциальная энергия системы «тело — Земля» равна П = m — g — h, если точечное тело массой m находится над повехносттью Земли на высоте h. Сказанное верно, если считать потенциальную энергию системы равной нулю, когда тело находится на поверхности Земли.
Силы упругой деформации и сила тяжести являются потенциальными силами. Силы трения не являются потенциальными.
Система тел, предоставленная самой себе, стремится уменьшить свою потенциальную энергию.
Чтобы потенциальная энергия системы тел не изменялась, необходимо, чтобы на части системы действовали внешние силы или силы трения, уравновешивающие внутренние потенциальные силы.
Вопросы
Что такое потенциальная энергия? Приведите примеры систем тел, обладающих потенциальной энергией. Может ли потенциальная энергия упруго деформированной пружины быть отрицательной? Может ли потенциальная энергия системы «тело — Земля» быть отрицательной? Ответы обоснуйте. Подсказка: чему равна потенциальная энергия системы тел «кирпич — Земля», если кирпич массой m лежит в яме на глубине l от поверхности Земли? Как называется единица потенциальной энергии в СИ? Приведите примеры потенциальных и непотенциальных сил. Может ли потенциальная энергия системы тел уменьшаться, увеличиваться, оставаться неизменной, если на тела системы не действуют внешние силы и силы трения? Приведите примеры.
Упражнения 1. Проанализируйте ситуацию, изображенную на рис. 128, ответив на вопросы: а) как изменяется потенциальная энергия растянутого шнура после отпускания прикрепленного к нему бруска? б) положительна или отрицательна работа силы упругости шнура?
в) как изменяется кинетическая энергия бруска?
2. Тело массой m переводят с начальной высоты h0 на конечную высоту hк, как показано на рис. 132. Рассмотрите каждый из случаев отдельно и ответьте на вопросы:
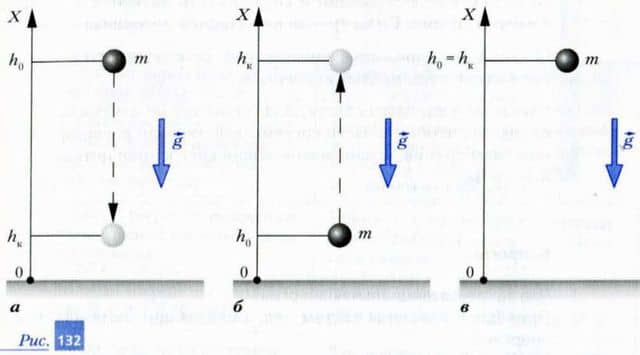а) чему равна начальная потенциальная энергия П0 системы «тело — Земля»? б) чему равна конечная потенциальная энергия системы «тело — Земля»? в) увеличивается или уменьшается потенциальная энергия системы «тело — Земля» при движении тела? г) чему равна разность начальной П0 и конечной Пк потенциальных энергий системы «тело — Земля»? д) чему равна работа силы тяжести при переводе тела из начального состояния в конечное?
е) равна ли работа силы тяжести разности начальной и конечной потенциальных энергий системы «тело — Земля»?
3. Определите изменение потенциальной энергии ΔП системы «камень — Земля» за время падения камня массой m = 5 кг с высоты h = 80 м.
4. Определите потенциальную энергию четырех пружин автомобиля жесткостью k = 2 кН/см каждая, удерживающих неподвижным кузов автомобиля массой m = 1 т, как показано на рис. 133. Модуль ускорения свободного падения считать равным g = 10 м/с2. 
(1 votes, average: 5,00 out of 5)