Первый закон термодинамики
1. Внутренняя энергия газа
Из курса физики основной школы вы знаете, что сумму кинетической энергии хаотического движения частиц и потенциальной энергии их взаимодействия называют внутренней энергией.
Внутренняя энергия U данной массы одноатомного идеального газа равна произведению средней кинетической энергии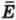 
одной молекулы на число молекул N:
U = 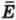N.
? 1. Объясните, почему внутренняя энергия U данной массы одноатомного идеального газа выражается формулой
? 2. Объем одного моля газа при температуре 20 ºС и нормальном атмосферном давлении составляет 24 л. а) Чему равна внутренняя энергия этого газа, если он одноатомный и его можно считать идеальным? б) На какую высоту можно было бы забросить мяч массой 365 г, если бы можно было сообщить ему такую кинетическую энергию и пренебречь сопротивлением воздуха?
Выполнив это задание, вы сможете представить, как велика внутренняя энергия тела. Объясняется это тем, что скорость хаотического движения молекул в десятки и сотни раз превышает скорости движения окружающих нас тел. А кинетическая энергия пропорциональна квадрату скорости.
Поэтому при увеличении скорости в 10 раз кинетическая энергия увеличивается в 100 раз, а при увеличении скорости в 100 раз кинетическая энергия увеличивается в 10 000 раз.
Внутреннюю энергию идеального одноатомного газа можно выразить также через его давление p и объем V.
? 3. Объясните, почему внутренняя энергия U данной массы одноатомного идеального газа выражается формулой
U = (3/2)pV. (2)
Подсказка. Воспользуйтесь формулой (1) и уравнением состояния идеального газа.
? 4. Из формулы (1) следует, что внутренняя энергия одного моля газа зависит только от его абсолютной температуры и количества вещества (числа молекул). А из формулы (2) следует, что она зависит от давления и объема, но зато не зависит от количества вещества. Объясните, почему тут нет противоречия.
? 5. Ширина класса 5 м, длина 10 м, а высота — 4 м. Температура воздуха 20 ºС, давление равно нормальному атмосферному давлению. а) Чему была бы равна внутренняя энергия газа, заполняющего класс, если бы он был одноатомным? (Воздух состоит в основном из двухатомных молекул. Как показывает расчет, выходящий за рамки нашего курса, внутренняя энергия двухатомного газа при тех же макроскопических параметрах в 5/3 раза больше, чем внутренняя энергия одноатомного газа.) б) На какую высоту можно было бы поднять автомобиль массой 1 т, затратив такую энергию?
в) Есть ли в условии лишние данные?
Результаты выполнения этого задания раскроют, какая огромная энергия «окружает» каждого из нас! А ведь мы ее практически не замечаем, считая воздух «пустотой».
Большую внутреннюю энергию имеют, конечно, и другие тела. Например, внутренняя энергия литра кипятка больше внутренней энергии того же литра воды при комнатной температуре на величину, равную работе, которую надо совершить для того, чтобы поднять легковой автомобиль на двенадцать этажей!
При изучении тепловых явлений мы учитываем только кинетическую энергию хаотического движения молекул и потенциальную энергию их взаимодействия. А ведь есть еще и во много раз большая энергия взаимодействия частиц в атомных ядрах. Вы знаете о ней из курса физики основной школы.
К ядерной физике мы вернемся в 11-м классе.
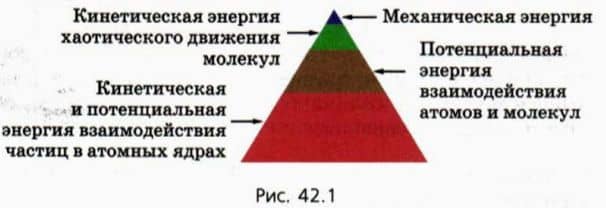
Соотношение между различными видами энергии, которыми обладает данное тело, схематически представлено на рисунке 42.1. Мы видим, что непосредственно наблюдаемая механическая энергия составляет лишь очень малую долю всей энергии тела. Соблюсти масштаб на этом рисунке невозможно, потому что тепловая внутренняя энергия в тысячи раз больше механической, а ядерная — в миллионы раз больше тепловой.
Два способа изменения внутренней энергии
Из курса физики основной школы вы знаете, что внутреннюю энергию тела можно изменить двумя способами:
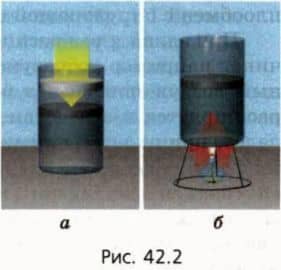
- Совершая работу над телом — например, сжимая газ (рис. 42.2, а); Посредством теплопередачи, то есть без совершения работы, — например, при контакте с более горячим телом (рис. 42.2, б). (Теплопередачу называют иногда также теплообменом.)
Напомним, что меру изменения внутренней энергии при теплопередаче называют количеством теплоты и обозначают Q. Количество теплоты измеряют в джоулях.
Как мы знаем, внутренняя энергия данной массы идеального газа определяется только его температурой и числом молекул. Поэтому при постоянном числе молекул изменить внутреннюю энергию идеального газа можно только изменив его температуру.
Например, при сжатии газа в теплоизолированном сосуде газ нагревается вследствие того, что над ним производят работу. Нагревание газа может быть при атом весьма заметным.
Поставим опыт
Поместим кусочек сухой ваты в толстостенный прозрачный цилиндр и быстро (резким толчком) вдвинем в цилиндр поршень (рис. 42.3). 
Воздух в цилиндре нагреется так сильно, что вата воспламенится.
Нагревание газа при сжатии используют в дизельных двигателях: при сжатии горючая смесь в цилиндре нагревается настолько, что воспламеняется без искры.
Газовый процесс, который происходит в теплоизолированном сосуде, то есть без теплопередачи, называют адиабатным. Адиабатным можно считать также процесс, когда тепло — передачей можно пренебречь: например, если процесс происходит за время, в течение которого не успевает произойти теплообмен с окружающей средой.
При адиабатном расширении газ охлаждается. По этой причине, например, образуются облака. Поднимающийся влажный воздух попадает в более разреженные слои атмосферы, расширяется и вследствие этого охлаждается.
Как мы увидим далее, при охлаждении ниже определенной температуры (точки росы) содержащийся в воздухе водяной пар конденсируется: образуются капельки тумана, из которого и состоят облака.
Увеличить или уменьшить температуру газа можно, конечно, и посредством теплопередачи. Например, сосуд с газом можно поместить над огнем, в кипящую воду или в морозильную камеру.
? 6. Изменяется ли, н если да, то как внутренняя энергия данной массы идеального газа: а) при изотермическом расширении? сжатии? б) при изобарном расширении? сжатии? в) при изохорном охлаждении? нагревании?
г) при адиабатном сжатии? расширении?
2. Первый закон термодинамики
Итак, внутренняя энергия газа U может изменяться как вследствие того, что ему сообщают количество теплоты Q, так и потому, что внешние силы совершают работу A над газом.
Согласно закону сохранения энергии
Изменение внутренней энергии газа ∆U равно сумме количества теплоты Q, переданного газу, и работы A, совершенной над газом:
∆U = Q + A. (3)
Закон сохранения энергии применительно к тепловым явлениям называют первым законом термодинамики. (Термодинамикой называют раздел физики, изучающий общие законы тепловых явлений.)
Как Q, так и A могут быть положительными, отрицательными или равными нулю. Если газ сжимают, то A > 0, а если он расширяется, то A < 0. Если объем газа не изменяется, то A = 0. Если газу передают некоторое количество теплоты, то Q > 0, а если газ отдает некоторое количество теплоты, то Q < 0.
В практических расчетах и при решении многих задач часто используют другую формулировку первого закона термодинамики. Дело в том, что при рассмотрении тепловых двигателей главный интерес представляет работа, совершенная самим газом (то есть силой давления, действующей со стороны газа на поршень; при расширении газа работа газа положительна).
Обозначим работу газа Aг. Она связана с работой A, совершенной внешними силами над газом, соотношением
Aг = — A.
При сжатии газа A > 0, Aг < 0; а при расширении газа A < 0, Aг > 0.
Используя понятие работы газа, первый закон термодинамики формулируют так:
Количество теплоты, переданное газу, равно сумме изменения внутренней энергии газа и работы, совершенной газом:
Q = ∆U + Aг. (4)
Чтобы использовать соотношения (3) и (4) на практике, надо уметь находить выражения для изменения внутренней энергии газа и работы газа (или работы внешних сил).
Как найти изменение внутренней энергии газа?
Для одноатомного идеального газа внутренняя энергия выражается формулой (1), поэтому для изменения ∆U внутренней энергии получаем:
∆U = (3/2)νR∆T. (5)
Здесь ∆T = T2 — T1, ∆U = U2 — U1, а индексами 1 и 2 обозначены соответственно начальное и конечное состояния газа.
? 7. Начальная температура пяти молей гелия 100 ºС. Газ нагрели на 50 ºС. а) Насколько увеличилась внутренняя энергия газа?
б) Есть ли в условии лишние данные?
Изменение внутренней энергии одноатомного идеального газа можно найти и с помощью формулы (2):
∆U = (3/2)∆(pV). (6)
Здесь ∆(pV) — изменение произведения давления на объем. Например, при переходе газа из состояния 1 в состояние 2
∆(pV) = p2V2 — p1V1. (7)
? 8. Чему равно изменение внутренней энергии одного моля одноатомного идеального газа: а) при изобарном расширении, если давление газа равно p0, а объем газа увеличился от V0 до 3V0? б) при изохорном охлаждении, если объем газа равен V0, а давление газа уменьшилось от p0 до 0,5p0? в) в процессе, в котором начальные давление и объем газа равны p0 и V0, а конечные равны 2p0 и 3V0?
Есть ли в условии лишние данные?
Важным достоинством формулы (6) является то, что в нее не входят ни количество вещества в газе, ни его масса. Поэтому, например, если давление и объем газа остались неизменными, то не изменилась и внутренняя энергия газа, хотя при этом могла измениться его масса. Рассмотрим пример, в котором речь идет о воздухе, который состоит в основном из двух — атомных молекул. Их средняя кинетическая энергия при заданной температуре больше, чем у одноатомных молекул (двухатомные молекулы обладают еще кинетической энергией вращательного движения).
Однако для выполнения следующего задания то, что воздух состоит из двухатомных молекул, несущественно.
? 9. До включения отопления температура воздуха в комнате объемом 60 м3 была равна 15 ºС. После включения отопления воздух нагрелся до 20 ºС. Давление воздуха постоянно и равно 105 Па.
а) На сколько процентов увеличилась средняя кинетическая энергия молекул в воздухе? б) Как изменилась внутренняя энергия воздуха в комнате? в) На сколько процентов изменилась концентрация молекул воздуха?
г) Насколько изменилась масса воздуха в комнате?
Как найти совершенную газом работу?
Рассмотрим сначала изобарное расширение газа в цилиндре под поршнем (рис. 42.4). Газ давит на поршень с силой F = pS, где p — давление газа, S — площадь поршня.
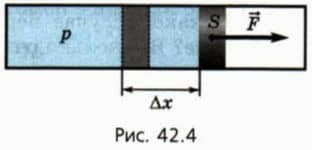Если поршень переместился на ∆x, то совершенная газом работа Aг = F * ∆x = pS * ∆x. Так как S * ∆x = ∆V, получаем, что при изобарном расшинерии работа газа выражается формулой
Aг = p * ∆V. (8)
? 10. Используя рисунок 42.5, объясните, почему работа газа численно равна площади фигуры под графиком зависимости p(V).
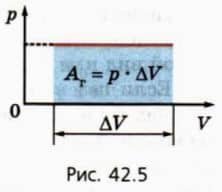Это свойство графика зависимости p(V) сохраняется и тогда, когда давление газа изменяется.
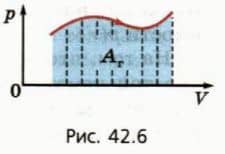
Пусть, например, график зависимости p(V) имеет вид, изображенный на рисунке 42.6. Процесс расширения газа мысленно разобьем на большое число этапов, в каждом из которых объем газа изменяется настолько мало, что его давление можно считать практически постоянным. Поскольку для каждого этапа работа газа численно равна площади под соответствующим участком графика, то и вся работа, совершенная газом при расширении, равна площади под всем графиком p(V).
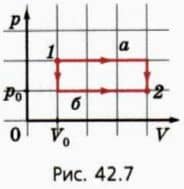
? 11. Один моль идеального газа можно перевести из состояния 1 в состояние 2 многими способами. Рассмотрим процессы, которым соответствуют графики а и б (рис.
42.7). а) В каком случае совершенная газом работа больше? Во сколько раз больше?
б) В каком случае изменение внутренней энергии газа больше? Во сколько раз больше? в) В каком случае переданное газу количество теплоты больше?
Во сколько раз больше?
На примере этого задания вы могли заметить, что изменение ∆U внутренней энергии данной массы идеального газа определяется только начальным и конечным состоянием газа.
Обусловлено это тем, что каждому состоянию данной массы газа (с определенными значениями p, V и T) соответствует одно определенное значение внутренней энергии, которое можно найти либо по формуле (1), либо по формуле (2).
А вот работа, совершенная газом при переходе из начального состояния в конечное, зависит от характера процесса, которым газ был переведен из начального состояния в конечное.
Действительно, работа газа численно равна площади под графиком зависимости p(V). А эта площадь зависит от того, какой вид имела функция p(V).
Если газ не расширяется, а сжимается (рис. 42.8), то внешние силы производят работу над газом. В таком случае говорят также, что газ производит отрицательную работу.
Она численно равна взятой со знаком минус площади S под графиком зависимости p(V).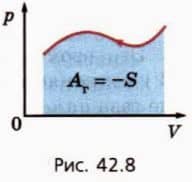 
На том, что работа газа зависит от вида зависимости p(V), а не только от начального и конечного состояния, основан принцип действия тепловых двигателей (в следующем параграфе мы рассмотрим их подробнее).
В тепловых двигателях газ расширяется при высокой температуре. При атом давление газа велико, поэтому он совершает большую работу. А сжимают газ при более низкой температуре, когда давление газа меньше.
Поэтому для того, чтобы вернуть газ в начальное состояние, внешние силы должны совершить меньшую работу.
Рассмотрим пример.
? 12. Газ совершает циклический процесс: переходит из состояния 1 в состояние 2 (рис. 42.9), а потом возвращается в состояние 1. При этом объем газа не должен быть меньше начального и больше конечного.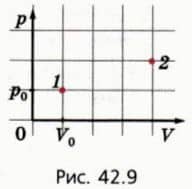 
а) Какую максимально возможную работу может совершить газ при переходе 1-2, если давление газа не должно превышать 3p0? б) Какую минимально возможную работу должны совершить внешние силы при переходе 2-1, если давление газа не должно быть меньше p0?
в) Насколько в этом случае работа газа при циклическом процессе больше работы внешних сил?
Применение первого закона термодинамики к изопроцессам и адиабатному процессу
? 13. Используя первый закон термодинамики, а также выражения для внутренней энергии и работы газа, объясните, почему: а) при изохорном процессе Aг = 0, Q = ∆U, то есть сообщенное газу количество теплоты (напомним, что оно может быть как положительным, так и отрицательным) равно изменению внутренней энергии газа; б) при изотермическом процессе ∆U = 0, Q = Aг, то есть сообщенное газу количество теплоты равно работе газа; в) при изобарном процессе Aг ≠ 0, ∆U ≠ 0; г) при адиабатном процессе Q = 0, Aг = -∆U, то есть при расширении газ совершает работу за счет уменьшения внутренней энергии, а при сжатии газа его внутренняя энергия увеличивается за счет работы внешних сил. Подсказка.
Если давление не изменяется, то ∆(pV) = p∆V.
Дополнительные вопросы и задания
14. На рисунках 42.10, а, б, в изображены графики трех процессов с данной массой одноатомного идеального газа. Чему равно изменение внутренней энергии газа для каждого из этих процессов при переходе 1-2?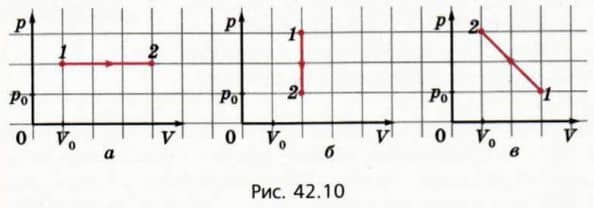 
15. При изобарном расширении данной массы одноатомного идеального газа его температура возросла от 0 ºС до 100 ºС. При этом газу было передано количество теплоты, равное 5 кДж. а) Насколько изменилась внутренняя энергия газа?
б) Чему равно количество вещества в сосуде с газом?
(1 votes, average: 5,00 out of 5)