Свойства пары сил
В учебниках физики описан такой способ определения центра тяжести: пластинку произвольной формы подвешивают на нитке за какую-нибудь ее точку (рис. 51). Когда установится равновесие, через эту точку подвеса проводят на пластинке вертикаль. Центр тяжести находится, конечно, на этой линии.
Потом пластинку подвешивают за другую точку. Проводят вертикальную линию, проходящую через эту точку. На пересечении двух линий и находится центр тяжести.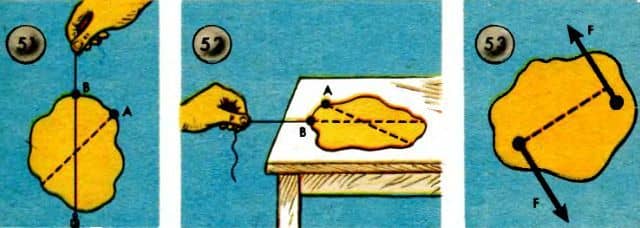 
Я проводил опыт иначе.
Прикрепим теперь нитку в другой точке и повторим опыт. Направление натянутой нити даст нам новую прямую, и в точке пересечения этих прямых находится центр тяжести пластинки.
Между этими способами имеется большое сходство. Но как объяснить такой поворот пластинки в моем опыте? Постараюсь объяснить этот вопрос так, чтобы вам все было понятно. Я расскажу вам про удивительные свойства пары сил. Знание этих свойств имеет огромное значение для техники.
Всюду: в машинах, станках, на заводе, на транспорте — вы видите, как вращаются валы, оси, шкивы. А чем вызывается вращение? Парой сил!
Даже когда вам кажется, что вращение происходит под действием только одной силы, например когда вы открываете или закрываете дверь за ручку, то в действительности и тут имеется пара сил — вторая сила возникает в петлях двери.
Парой сил или просто парой в механике называют две равные по модулю, параллельные, противоположно направленные силы, приложенные к телу таким образом, чтобы они не оказались на одной прямой (рис. 53). Равнодействующей пара сил не имеет.
Под действием пары сил тело вращается. И уравновесить пару одной силой нельзя. Для этого потребуется другая пара сил, которая бы вращала тело в обратную сторону.
Конечно, вращающее действие этой второй пары должно быть равно вращающему действию первой. А от чего зависит вращающее действие пары сил? Конечно, от модуля сил, составляющих пару сил.
Но не только от этого. Вращающее действие пары зависит и от расстояния между силами, составляющими пару. Чтобы увеличить действие пары сил, буравы, винтовые прессы и т. п. снабжают рукоятками (рис. 54), и, чем длиннее рукоятка, чем больше будет расстояние между силами, тем большим будет вращающее действие пары.
Расстояние между параллельными силами пары (по перпендикулярному к ним направлению) называют плечом пары сил.
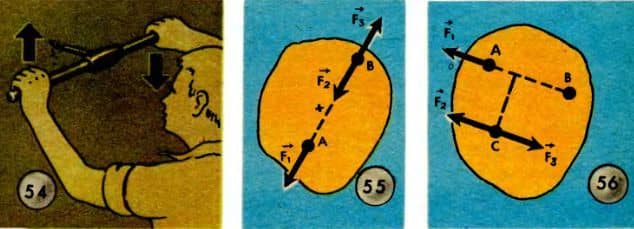
Вращающее действие пары измеряют произведением модуля силы на плечо. Такое произведение называют моментом пары.
Здесь уместно немного поговорить о слове «момент». Дело в том, что это слово в обычной разговорной речи и в механике имеет совсем разные значения. В разговорной речи «момент» означает «очень короткий промежуток времени». Так, например, говорят: «в один момент», «моментально».
В механике же термин «момент» имеет иное значение; оно не связано с понятием времени. В переводе с латинского momentum означает «движущая сила», «толчок»; в английской литературе слово momentum переводится как «импульс». Однако в русской научной литературе это слово связывают не с импульсом, а с вращением.
Рассматривая вращающиеся тела, используют понятия «момент силы», «момент импульса» («момент количества движения»), «момент инерции». При этом часто «момент силы» для краткости называют просто «моментом». Помня об этом, не удивляйтесь, почему при расчетах балок, осей важно находить «изгибающие моменты», при расчете валов — «крутящие моменты» и т. д.
Момент сил вы изучали в школе и даже решали задачи на равновесие рычагов, используя правило моментов. Я уже говорил, что и при действии одной силы, если она не проходит через ось вращения тела, мы имеем в сущности пару сил. Вторая сила возникает в качестве противодействия оси телу, деформирующему ось.
Ведь если бы не было оси, то тело стало бы удаляться под действием приложенной силы. Ось же удерживает его.
Встречающееся определение, согласно которому плечом силы называется перпендикуляр, опущенный из оси вращения на линию действия силы, полностью совпадает с определением плеча пары сил как кратчайшего расстояния между параллельными силами, составляющими пару.
Теперь я предложу вам новый вопрос: что вы знаете о переносе точки приложения силы?
Точку приложения силы можно переносить по линии действия силы. Мы хотим перенести точку приложения силы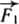 
из точки A в точку B (рис. 55). Приложим в точке B две противоположные силы 
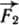и 
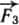, равные по модулю силе .
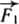Это не окажет никакого влияния на тело: ведь силы уравновешены. Но можно считать, что уравновешены и силы 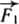и 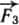. Значит, их можно отбросить и тогда останется только сила 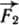, равная по модулю силе 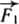и так же направленная, но приложенная в точке B.
А теперь я покажу вам, что случится, если мы перенесем силу 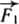не в точку B на линии действия силы, а в какую-нибудь точку C вне этой линии (рис. 56). Будем рассуждать так.
Приложим в точке C две силы, равные по модулю и параллельные силе 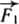. Можно ли теперь отбросить силы 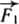и 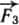, как это только что делали? Конечно нет!
Это не уравновешенные силы, это пара сил, и она должна вызывать вращение тела.
Итак, если силу перенести не по линии ее действия, это не проходит безнаказанно: появляется еще так называемая «присоединенная пара». Действие этой пары тем больше, чем дальше в сторону от линии AB мы выбираем точку C, потому что силы-то те же, но плечо, а значит, и момент больше. В случае если точку приложения выбрать на линии действия сил, плечо обращается в нуль и никакой пары не присоединяется.
Вот почему и говорят, что точку приложения силы можно переносить только по линии действия силы.
Пары, имеющие равные моменты, называются эквивалентными парами (рис. 57).
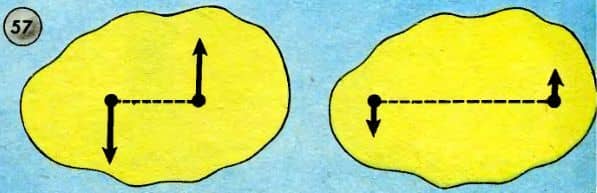
Я могу вам доказать, что в отличие от одной силы пару можно переносить в любое место плоскости, в которой она расположена, и притом совершенно безнаказанно. При этом не обязательно даже сохранять прежнее направление сил, т. е. пару можно поворачивать как угодно, лишь бы момент пары и направление вращения, ею вызываемого (по или против часовой стрелки), оставались прежними.
Вот смотрите: приложим в точках C и D (|CD| = |AB|) по две противоположные силы, т. е. как бы две противоположные пары. Одна из них, отмеченная черточками (рис. 58, а), стремится вращать тело в одну сторону, другая — в противоположную. Следовательно, пары уравновешиваются, но можно считать уравновешенными и первоначальную пару с плечом AB, и противоположную ей с плечом CD (перечеркнутую).
Тогда останется лишь одна пара с плечом CD, вращающая тело в ту же сторону, что и первоначальная. Значит, можно сказать, что мы пару с плечом AB перенесли на плечо CD. Разве это не удивительное свойство пары сил?
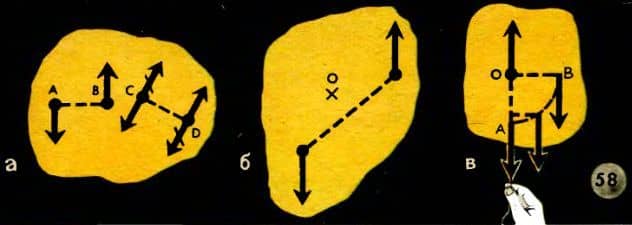
Неужели новая пара действует так же, как первоначальная? Ведь ось-то вращения тоже переместилась? Всякая пара сил, где бы она ни была расположена в той же плоскости, вращает тело вокруг оси, проходящей через центр тяжести (центр масс) тела, т. е. через току O (рис. 58, б).
Вот еще одно удивительное свойство пары сил.
Но почему же?! Какое отношение имеет к этому всему центр тяжести? Дело в том, что пара сил не имеет равнодействующей.
Следовательно, в этом случае не удастся свести движение тела к движению центра тяжести. Поскольку на центр тяжести не действует никакая сила, то он должен оставаться в покое, быть неподвижным. Других неподвижных точек у тела быть не может, так как две неподвижные точки, не лежащие на оси вращения, не позволили бы телу вращаться.
Значит, где же проходит ось вращения (ведь ось вращения неподвижна)? Только через центр тяжести и нигде больше! Если направление приложенной силы не проходит через центр тяжести, то мы можем ее перенести, как я объяснял, в центр тяжести, но тогда появится присоединенная пара.
Тело начнет поворачиваться, как вы и видели на опыте (см. рис. 52). При этом плечо пары и ее момент будут все уменьшаться (рис. 58, в), пока направление тянущей нити не станет проходить через центр тяжести.
Тогда вращение прекратится и тело будет двигаться поступательно.
Вот и все, что я хотел рассказать вам об удивительных свойствах пары сил. То, что вы узнали, имеет большое значение в технике. Для плавного хода машин необходимо, чтобы вращающиеся части были хорошо уравновешены (балансированы), т. е. чтобы ось вращения проходила через центр масс вала, шкива, якоря электрического генератора или двигателя, иначе установка будет вибрировать и может разрушиться.
(1 votes, average: 5,00 out of 5)