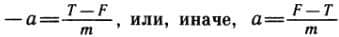«Математические начала натуральной философии»
В 1642 году умер Галилей, в 1643 году родился Ньютон. В 1687 году была издана гениальная книга Ньютона «Математические начала натуральной философии».
Титульный лист этой книги изображен на рисунке 33. Академик С. И. Вавилов в биографии Ньютона писал: «В истории естествознания не было события более крупного, чем появление «Начал» Ньютона. Причина была в том, что эта книга подводила итоги всему сделанному за предшествующие тысячелетия в учении о простейших формах движения материи». «…Возникла «классическая физика» по образу
Что же это за книга, получившая такой восторженный отзыв? Кто был ее автор? Надгробная эпитафия так отвечает на второй вопрос:
«Здесь покоится сэр Исаак Ньютон, дворянин, который… первый доказал с факелом математики движение планет, пути комет и приливы океанов.
Он исследовал различие световых лучей и проявляющиеся при этом различные свойства цветов, чего ранее никто не подозревал….Пусть смертные радуются, что существовало такое украшение рода человеческого».
Попытаемся очень кратко рассказать о Ньютоне. Личная жизнь Ньютона была не богата событиями. На ней, по-видимому, не отразились политические бури, которые потрясали в тот век его родину.
А между тем в Англии за долгую, восьмидесятилетнюю жизнь Ньютона произошли две революции, сменилось шесть королей. Ньютон был современником Петра 1 и Людовика XIV.
Окончив университет, Ньютон получил ученое звание бакалавра, затем магистра. С 1669 года стал во главе кафедры физики и математики в Кембриджском университете. Внешне жизнь Ньютона протекала спокойно, мирно и однообразно.
Но ее заполняли непрестанный труд, математические изыскания, физические и химические опыты, вызывавшие восхищение его современников. Имя Ньютона еще при жизни было окружено ореолом национального героя.
Плодами его неутомимой деятельности явились «Метод флюксий и бесконечные ряды» (основы дифференциального и интегрального исчисления — по принятой теперь терминологии), «Оптика» и «Математические начала натуральной философии», определившие все дальнейшее развитие науки. Давая общую оценку роли Ньютона в науке, академик С. И. Вавилов писал: «На всей физике лежал отпечаток его мысли, без Ньютона наука развивалась бы иначе».
«Математические начала натуральной философии». Почему так назвал свою книгу Ньютон? Название «натуральная философия» в значении «физика» сохранилось в английском языке до сих пор (наряду с термином physics).
Это название довольно точно передает содержание физики как науки, изучающей простейшие и наиболее общие свойства материи и формы ее движения.
Заметьте, что по-английски physic (без s) означает «медицина».
Почему эти «Начала» математические?
Ньютон, великий физик, был в то же время не менее великим математиком, физику он хотел построить по образу и подобию геометрии: из нескольких аксиом (принципов, основных положений), представляющих обобщение многовекового опыта человечества, математическим путем вывести теоремы и правила.
Замысел «Начал» — доказать, что закон всемирного тяготения неизбежно вытекает из применения принципов механики к движениям небесных тел. Книга состоит из трех частей. Во введении читатель найдет определения основных физических понятий: массы, количества движения, силы и др. Эти понятия сопровождаются соответствующими пояснениями или «поучениями».
Затем следуют аксиомы, или законы движения. Каждый из трех законов, как и каждое определение, сопровождается пояснениями, затем идут следствия из закона н общее «поучение». В первой части, или первой книге, Ньютон описал движения тел под влиянием только отдельных сил, во второй части — те же движения в сопротивляющейся среде.
Первая и вторая книги представляют собой энциклопедию физических знаний того времени. Написав первые две части, Ньютон хотел на этом остановиться. Но для большинства современников Ньютона в таком виде она осталась бы малопонятной, поэтому ученым была написана третья часть — «О системе мира».
Книгу читать нелегко. Сам Ньютон рекомендовал лицам, не имеющим глубоких математических знаний, ограничиться выборочным чтением. «Достаточно,- пишет он,- если кто тщательно прочтет определения, законы движения и первые три отдела 1-й книги и затем перейдет к 3-й книге о системе мира; из прочих же предложений предыдущих книг, если того пожелает, будет справляться в тех, на которые есть ссылки».
Повторим три основных закона Ньютона.
«Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние». Это дословная формулировка закона, записанная в «Началах» самим Ньютоном. Но все ли понятно в такой формулировке? Что означают, например, слова «пока и поскольку»?
Даже академик А. Н. Крылов, переводя этот закон с латинского языка на русский, признавал, что ему трудно было подобрать русские слова для глубоко выразительной мысли Ньютона, записанной по-латыни. По Ньютону, этот закон объединяют два понятия: стойкость, или упорство, в сохранении телом данного состояния и продолжительность сохранения этого состояния. Разделив эти понятия, можно было бы сформулировать два закона:
«Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не изменят этого состояния».
«Всякое тело удерживает свое состояние покоя или равномерного и прямолинейного движения, поскольку оно не понуждается приложенными силами изменить это состояние».
Сейчас мы набегаем приписывать телам какое-то «упорство» и формулируем первый закон Ньютона так: «Всякое тело сохраняет состояние покоя или равномерного и прямолинейного движения, если действие со стороны других тел не изменяет этого состояния».
Можно самим сконструировать приборы, подобрать интересные примеры из техники о применении законов Ньютона, составить задачи. На рисунке 34 изображен простой прибор, иллюстрирующий первый закон Ньютона, согласно которому свободное движение тела может происходить только по прямой линии, в направлении вектора скорости. Прибор действует так: под действием упругой силы сжатой пружины шарик по инерции движется в горизонтальной плоскости от трубки А до трубки В. Движение по инерции — это движение по прямой линии. Трубка В изогнута по дуге окружности. Поэтому шарик, пройдя трубку В, дальше движется по касательной к этой окружности и попадает в трубку С. Теперь ответьте на такие вопросы: «Неужели тело движется равномерно и прямолинейно только в том случае, когда на него совсем не действуют силы?», «Почему практически равномерно и прямолинейно перемещает сеялку трактор?»
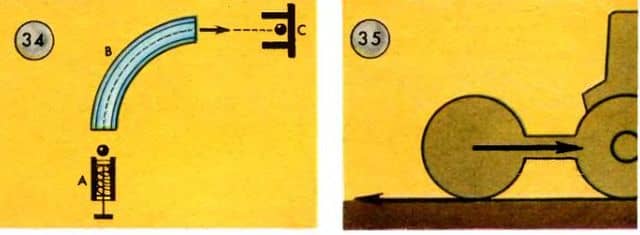— Трактор передвигает сеялку равномерно и прямолинейно, если сила тяги равна по модулю силе преодолеваемого трения (рис. 35) . Вообще, если на тело действуют уравновешенные силы, то тело будет оставаться в покое или двигаться равномерно и прямолинейно. В этом случае нет причины, которая изменяла бы движение, т. е. изменяла бы скорость по модулю или направлению.
Обратимся ко второму закону Ньютона. «Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение», говорится в учебнике. Ньютон несколько по-другому сформулировал этот закон: «Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует». Импульсом (количеством движения) называется произведение массы тела на скорость. Математически второй закон Ньютона можно записать так:
Δ(mv) = FΔt
Знак Δ (дельта) обозначает малое изменение (приращение или убыль) чего-нибудь. Так Δ(mv) есть изменение импульса, F — постоянная сила, Δt — приращение, или промежуток времени, в течение которого происходит данное изменение импульса.
Третий закон Ньютона иногда формулируют так: «Всякому действию всегда есть равное и прямо противоположное противодействие». Как это понимать? Предположим, что тело А действует на тело Б с силой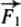 
. Согласно третьему закону Ньютона должна обязательно существовать ответная сила — 
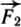, с какой тело Б действует на тело А. При этом сила 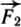равняется по модулю силе 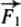, но имеет противоположное направление: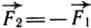 
Подчеркнем, что рассматриваемые силы приложены к разным телам: сила 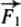приложена к телу Б, а сила 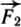к телу А. Поэтому было бы ошибочно полагать, что эти силы, складываясь, взаимно уничтожаются. Ведь складывать можно лишь силы, приложенные к одному и тому же телу. 
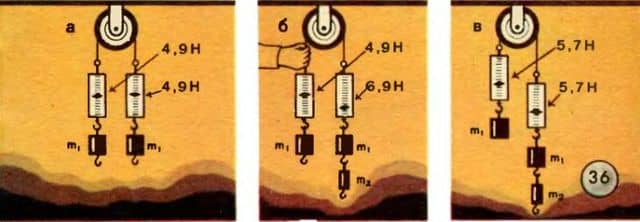Второй и третий законы Ньютона можно продемонстрировать на следующем приборе (рис.
36). Через блок перекинута нить, к концам которой подвешены динамометры, а к динамометрам одинаковые грузы массой m1 =0,5 кг каждый. Массой динамометров будем пренебрегать, полагая, что эта масса не превышает нескольких граммов. Система грузов уравновешена и неподвижна. Каждый динамометр фиксирует силу m1g=4,9 Н (рис.
36, а). Подвесим к правому грузу дополнительный груз массой m2=0,2 кг. Если при этом удерживать нить рукой так, чтобы система грузов оставалась неподвижной, то правый динамометр зафиксирует силу (m1 + m2)g=6,9 Н, тогда как левый будет по-прежнему показывать 4,9 Н (рис. 36, б). Если же убрать руку, то система грузов начнет двигаться с некоторым ускорением; при этом показания обоих динамометров будут одинаковыми и, как показывает опыт, будут составлять 5,7 Н (рис.
36, в). Чтобы объяснить этот результат, надо воспользоваться законами Ньютона.
Сначала найдем ускорение a рассматриваемой системы. Она ускоряется под действием силы тяжести дополнительного груза, т. е. под действием силы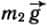 
. Масса всей системы грузов равна 2m1 + m2.
Согласно второму закону Ньютона получаем, что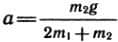 
Будем рассматривать правый груз m1 и дополнительный груз m2 как единое тело. Силы, приложенные к этому телу, показаны на рисунке 37 слева. Этих сил две: сила тяжести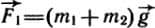 
и сила 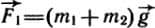с которой динамометр действует на рассматриваемое тело.
По третьему закону Ньютона с такой же по модулю силок тело действует на динамометр; следовательно, сила T1 соответствует показанию правого динамометра. Используя рисунок, запишем в соответствии со вторым законом Ньютона:
F1 — T1 = (m1 + m2)a
Отсюда следует, что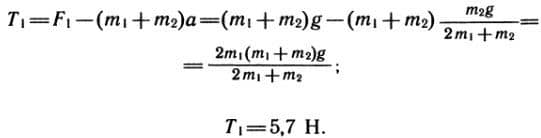 
Теперь рассмотрим левый груз массой m1.
Силы, приложенные к нему, показаны на рисунке 37 справа;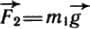 
, сила T2 соответствует показанию левого динамометра. Согласно второму закону Ньютона
T2 — F2 = m1a.
Отсюда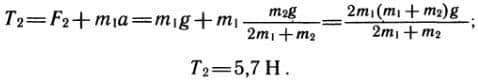 
Как и следовало ожидать, T1 = T2. Это объясняется тем, что массами динамометров мы пренебрегали и, кроме того, полагали, что натяжение нити одинаково по обеим сторонам блока.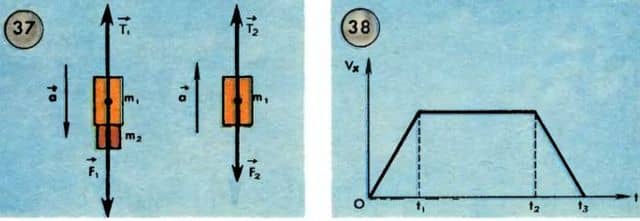 
Заметим, что вопрос о натяжении нити, шнура или троса не простой. Поэтому в заключение мы решим с вами еще одну задачу. Запишите ее условие.
«Определить силу натяжения каната в начале подъема кабины лифта, при установившемся равномерном движении, в конце подъема. Масса кабины с пассажирами 1500 кг. Ускорение кабины в начале и конце подъема одинаково и по модулю равно 1,7 м/с2».
Зачем здесь дано ускорение, почему лифт идет то ускоренно, то равномерно? При посадке пассажиров лифт был неподвижен, т. е. начальная скорость его была равна нулю. Чтобы достичь какой-то скорости о, необходимо некоторое время. Как бы мало оно ни было, движение за этот промежуток времени было ускоренным; оно характеризовалось ускорением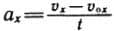 
.
Вот об этом ускорении и сказано в условии задачи, что оно равно 1,7 м/с2. Точно так же и остановка никогда не бывает мгновенной, какие бы тормоза ни замедляли движение.
На рисунке 38 изображен график скорости поднимающейся кабины лифта. В течение промежутка времени от 0 до t1 движение кабины равноускоренное; от t1 до t2 кабина движется равномерно; от t2 до t3 кабина движется равнозамедленно. В момент времени t3 кабина останавливается.
На кабину лифта действуют две силы: сила тяжести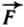 
(ока направлена вертикально вниз) и сила натяжения 
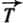со стороны каната (она направлена вверх). По третьему закону Ньютона кабина лифта действует на канат с силой, модуль которой равен модулю силы, с которой канат действует на кабину. Это и есть искомая сила натяжения каната.
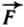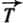Когда кабина лифта движется равномерно, силы и , приложенные к кабине, взаимно уравновешены; в атом случае
T = F = mg; T = 1500 * 9,8 м/с2 = 14700 H.
В начале подъема кабина имеет ускорение a=1,7 м/с2. Согласно второму закону Ньютона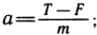 
следовательно,
T = F + ma; T = 14700 Н + 1500 кг * 1,7 м/с2 = 17250 Н.
В конце подъема кабина движется равнозамедленно. Это означает, что, хотя она продолжает двигаться вверх, однако ее ускорение направлено при этом вниз. В данном случае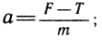 
следовательно,
T = F — ma; T = 14700 Н — 1500 кг * 1,7 м/с2 = 12150 Н.
Заметим, что равенства 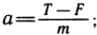и 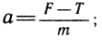могут быть записаны единым образом, если воспользоваться векторами: 
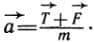Спроецируем это векторное равенство на ось координат, направленную вертикально вверх.
Проекция вектора 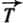есть, очевидно, T, а проекция вектора 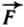есть — F. Что касается вектора 
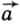, то в начале подъема лифта он направлен вверх и, следовательно, его проекция есть A, тогда как в конце подъема этот вектор направлен вниз и, следовательно, его проекция есть — a. В первом случае получаем:
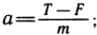а во втором случае получаем: 
(1 votes, average: 5,00 out of 5)