Импульс. Закон сохранения импульса
1. Импульс
В некоторых случаях удается исследовать взаимодействие тел, не используя выражения для сил, действующих между телами. Это возможно благодаря тому, что существуют физические величины, которые остаются неизменными (сохраняются) при взаимодействии тел. В этой главе мы рассмотрим две такие величины — импульс и механическую энергию.
Начнем с импульса.
Физическую величину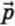 
, равную произведению массы тела m на его скорость 
, называют импульсом тела (или
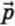= m.
Импульс — векторная величина. Модуль импульса p = mv, а направление импульса совпадает с направлением скорости тела. Единицей импульса является 1 (кг * м)/с.
? 1. По шоссе в направлении на север со скоростью 40 км/ч едет грузовик массой 3 т. В каком направлении и с какой скоростью должен ехать легковой автомобиль массой 1 т, чтобы его импульс был равен импульсу грузовика?
? 2. Мяч массой 400 г свободно падает без начальной скорости с высоты 5 м, После удара мяч отскакивает вверх, причем модуль скорости мяча в результате удара не изменяется. а) Чему равен и как направлен импульс мяча непосредственно перед ударом? б) Чему равен и как направлен импульс мяча сразу после удара? в) Чему равно и как направлено изменение импульса мяча в результате удара? Найдите изменение импульса графически.
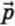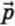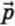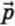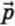Подсказка. Если импульс тела был равен 1, а стал равен 2, то изменение импульса ∆ = 2 — 1.
2. Закон сохранения импульса
Важнейшим свойством импульса является то, что при определенных условиях суммарный импульс взаимодействующих тел остается неизменным (сохраняется).
Поставим опыт
Две одинаковые тележки могут катиться по столу вдоль одной прямой практически без трения. (Этот опыт можно поставить при наличии современного оборудования.) Отсутствие трения — важное условие нашего опыта!
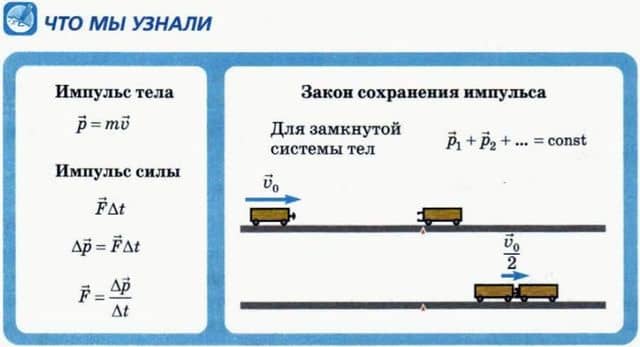
Установим на тележках защелки, благодаря которым тележки после столкновения движутся как одно тело. Пусть правая тележка вначале покоится, а левой толчком сообщим скорость 0 (рис. 25.1, а).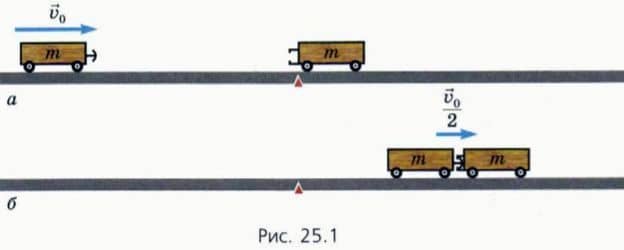 
После столкновения тележки движутся вместе. Измерения показывают, что их общая скорость в 2 раза меньше, чем начальная скорость левой тележки (25.1, б).
Обозначим массу каждой тележки m и сравним суммарные импульсы тележек до и после столкновения.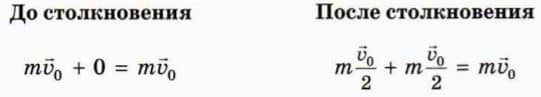 
Мы видим, что суммарный импульс тележек остался неизменным (сохранился).
Может быть, это справедливо только тогда, когда тела после взаимодействия движутся как единое целое?
Поставим опыт Заменим защелки на упругую пружину и повторим опыт (рис. 25.2).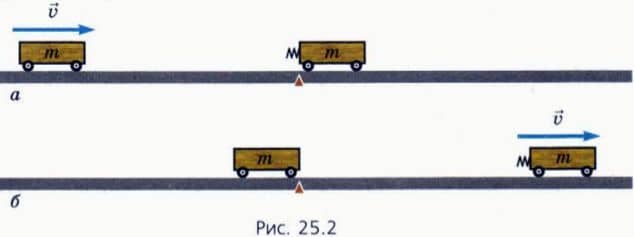 
На этот раз левая тележка остановилась, а правая приобрела скорость, равную начальной скорости левой тележки.
? 3. Докажите, что и в этом случае суммарный импульс тележек сохранился.
Может быть, это справедливо только тогда, когда массы взаимодействующих тел равны?
Поставим опыт Закрепим на правой тележке еще одну такую же тележку и повторим опыт (рис. 25.3).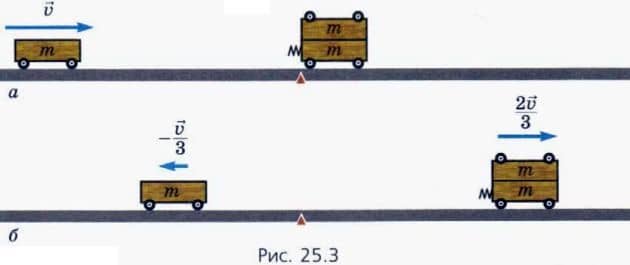 
Теперь после столкновения левая тележка стала двигаться в противоположном направлении (то есть влево) со скоростью, равной —/3, а сдвоенная тележка стала двигаться вправо со скоростью 2/3.
? 4. Докажите, что и в этом опыте суммарный импульс тележек сохранился.
Чтобы определить, при каких условиях суммарный импульс тел сохраняется, введем представление о замкнутой системе тел. Так называют систему тел, которые взаимодействуют только друг с другом (то есть не взаимодействуют с телами, не входящими в эту систему).
В точности замкнутых систем тел в природе не существует — хотя бы потому, что невозможно «отключить» силы всемирного тяготения.
Но во многих случаях систему тел с хорошей точностью можно считать замкнутой. Например, когда внешние силы (силы, действующие на тела системы со стороны других тел) уравновешивают друг друга или ими можно пренебречь.
Именно так и было в наших опытах с тележками: действующие на них внешние силы (сила тяжести и сила нормальной реакции) уравновешивали друг друга, а силой трения можно было пренебречь, Поэтому скорости тележек изменялись только вследствие их взаимодействия друг с другом.
Описанные опыты, как и многие другие, подобные им, свидетельствуют о том, что выполняется Закон сохранения импульса: векторная сумма импульсов тел, составляющих замкнутую систему, не изменяется при любых взаимодействиях между телами системы: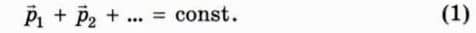 
Закон сохранения импульса выполняется только в инерциальных системах отсчета.
Закон сохранения импульса как следствие законов Ньютона
Покажем на примере замкнутой системы двух взаимодействующих тел, что закон сохранения импульса — следствие второго и третьего законов Ньютона.
Обозначим массы тел m1 и m2, а их начальные скорости 1 и 2. Тогда векторная сумма импульсов тел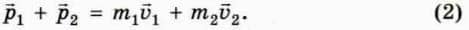 
Пусть в течение промежутка времени ∆t взаимодействующие тела двигались с ускорениями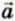 
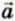1 и 2.
? 5. Объясните, почему изменение суммарного импульса тел можно записать в виде
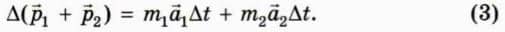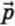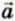Подсказка. Воспользуйтесь тем, что для каждого тела ∆ = m∆, а также тем, что ∆ = ∆t.
? 6. Обозначим 
1 и 2 силы, действующие соответственно на первое и второе тело. Докажите, что
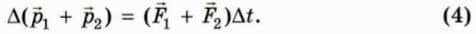Подсказка. Воспользуйтесь вторым законом Ньютона и тем, что система замкнута, вследствие чего ускорения тел обусловлены только силами, с которыми эти тела действуют друг на друга.
? 7. Докажите, что
Подсказка. Воспользуйтесь третьим законом Ньютона.
Итак, изменение суммарного импульса взаимодействующих тел равно нулю. А если изменение некоторой величины равно нулю, то это означает, что эта величина сохраняется.
? 8. Почему из приведенного рассуждения следует, что закон сохранения импульса выполняется только в инерциальных системах отсчета?
3. Импульс силы
Есть такая поговорка: «Знать бы, где упадешь, — соломки постелил бы». А зачем нужна «соломка»? Почему спортсмены на тренировках и соревнованиях падают или прыгают на мягкие маты, а не на твердый пол? Почему после прыжка надо приземляться на согнутые ноги, а не на выпрямленные? Зачем в автомобилях нужны ремни и подушки безопасности?
Мы сможем ответить на все эти вопросы, познакомившись с понятием «импульс силы».
Импульсом силы называют произведение силы на промежуток времени ∆t, в течение которого действует эта сила.
Название «импульс силы» не случайно «перекликается» с понятием «импульс». Рассмотрим случай, когда на тело массой m в течение промежутка времени ∆t действует сила .
? 9. Докажите, что изменение импульса тела ∆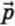 равно импульсу действующей на это тело силы:
Подсказка. Воспользуйтесь тем, что ∆ = m∆, и вторым законом Ньютона.
Перепишем формулу (6) в виде 
Эта формула представляет собой другую форму записи второго закона Ньютона. (Именно в таком виде сформулировал этот закон сам Ньютон.) Из нее следует, что на тело действует большая сила, если его импульс существенно изменяется за очень краткий промежуток времени ∆t.
Вот почему при ударах и столкновениях возникают большие силы: удары и столкновения характеризуются как раз малым интервалом времени взаимодействия.
Чтобы ослабить силу удара или уменьшить силы, возникающие при столкновении тел, надо удлинить промежуток времени, в течение которого происходит удар или столкновение.
? 10. Объясните смысл поговорки, приведенной в начале этого раздела, а также ответьте на другие вопросы, помещенные в том же абзаце.
? 11. Мяч массой 400 г ударился о стену и отскочил от нее с той же по модулю скоростью, равной 5 м/с. Перед самым ударом скорость мяча была направлена горизонтально. Чему равна средняя сила давления мяча на стену, если он соприкасался со стеной в течение 0,02 с?
? 12.Чугунная болванка массой 200 кг падает с высоты 1,25 м в песок и погружается в него на 5 см. а) Чему равен импульс болванки непосредственно перед ударом? б) Чему равно изменение импульса болванки за время удара?
в) Сколько времени длился удар? г) Чему равна средняя сила удара?
Дополнительные вопросы и задания
13. Шарик массой 200 г движется со скоростью 2 м/с влево. Как должен двигаться другой шарик массой 100 г, чтобы суммарный импульс шариков был равен нулю?
14. Шарик массой 300 г равномерно движется по окружности радиусом 50 см со скоростью 2 м/с. Чему равен модуль изменения импульса шарика: а) за один полный период обращения? б) за половину периода обращения? в) за 0,39 с?
15. Первая доска лежит на асфальте, а вторая такая же — на рыхлом песке. Объясните, почему в первую доску легче забить гвоздь, чем во вторую?
16. Пуля массой 10 г, летевшая со скоростью 700 м/с, пробила доску, после чего скорость пули стала равной 300 м/с. Внутри доски пуля двигалась в течение 40 мкс. а) Чему равно изменение импульса пули вследствие прохождения сквозь доску?
б) С какой средней силой пуля действовала на доску при прохождении сквозь нее?
(1 votes, average: 5,00 out of 5)