О движении бросаемых тел
В 1638 г. в Лейдене вышла книга Галилея «Беседы и математические доказательства, касающиеся двух новых отраслей науки». Четвертая глава этой книги называлась «О движении бросаемых тел». Не без труда удалось ему убедить людей в том, что в безвоздушном пространстве «крупинка свинца должна падать с такой же быстротой, как пушечное ядро». Но когда Галилей поведал миру о том, что ядро, вылетевшее из пушки в горизонтальном направлении, находится в полете столько же времени, что и ядро, просто выпавшее из ее жерла на землю, ему не поверили.
Между
Чтобы убедиться в этом, воспользуемся прибором, принцип действия которого иллюстрирует рисунок 104, а. После удара молоточком М по упругой пластине П шарики начинают падать и, несмотря на различие в траекториях, одновременно достигают земли. На рисунке 104, б изображена стробоскопическая фотография падающих шариков. Для получения этой фотографии опыт проводили в темноте, а шарики через равные интервалы времени освещали яркой вспышкой света.
При этом затвор фотоаппарата был открыт до тех пор, пока шарики не упали на землю. Мы видим, что в одни и те же моменты времени, когда происходили вспышки света, оба шарика находились на одной и той же высоте и столь же одновременно они достигли земли. 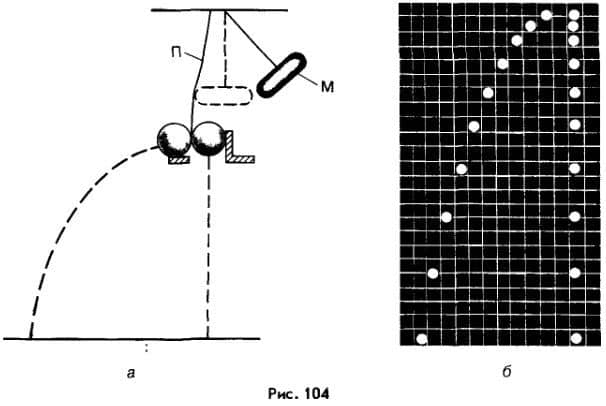
Время свободного падения с высоты h (вблизи поверхности Земли) может быть найдено по известной из механики формуле s = at2/2. Заменяя здесь s на h и a на g, перепишем эту формулу в виде
H = (gt2)/2,
Откуда после несложных преобразований получим
T = √(2h/g) (44.1)
Такое же время будет находиться в полете и тело, брошенное с той же высоты в горизонтальном направлении. В этом случае, согласно Галилею, «к равномерному беспрепятственному движению присоединяется другое, вызываемое силой тяжести, благодаря чему возникает сложное движение, слагающееся из равномерного горизонтального и естественно ускоренного движений».
За время, определяемое выражением (44.1), двигаясь в горизонтальном направлении со скоростью v0 (т. е. с той скоростью, с которой оно было брошено), тело переместится по горизонтали на расстояние
L = v0t = v0√(2h/g) (44.2)
Из этой формулы следует, что дальность полета тела, брошенного в горизонтальном направлении, пропорциональна начальной скорости тела и возрастает с увеличением высоты бросания.
Чтобы выяснить, по какой траектории движется в этом случае тело, обратимся к опыту. Присоединим к водопроводному крану резиновую трубку, снабженную наконечником, и направим струю воды в горизонтальном направлении. Частицы воды при этом будут двигаться точно так же, как и брошенное в том же направлении тело. Отворачивая или, наоборот, заворачивая кран, можно изменить начальную скорость струи и тем самым дальность полета частиц воды (рис.
105), однако во всех случаях струя воды будет иметь форму параболы. Чтобы убедиться в этом, позади струи следует поставить экран с заранее начерченными на нем параболами. Струя воды будет точно соответствовать изображенным на экране линиям. 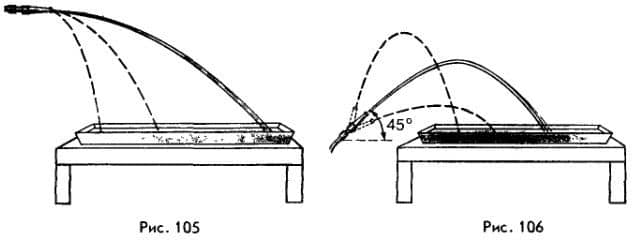
Итак, свободно падающее тело, начальная скорость которого горизонтальна, движется по параболической траектории.
По параболе будет двигаться тело и в том случае, когда оно брошено под некоторым острым углом к горизонту. Дальность полета в этом случае будет зависеть не только от начальной скорости, но и от угла, под которым она была направлена. Проводя опыты со струей воды, можно установить, что наибольшая дальность полета при этом достигается тогда, когда начальная скорость составляет с горизонтом угол 45° (рис.
106).
При больших скоростях движения тел следует учитывать сопротивление воздуха. Поэтому дальность полета пуль и снарядов в реальных условиях оказывается не такой, как это вытекает из формул, справедливых для движения в безвоздушном пространстве. Так, например, при начальной скорости пули 870 м/с и угле 45° в отсутствие сопротивления воздуха дальность полета составила бы примерно 77 км, между тем как в действительности она не превышает 3,5 км.
??? 1. Какая пуля упадет на землю раньше: вылетевшая при выстреле из горизонтально расположенного ружья или случайно оброненная с той же высоты в момент выстрела из ружья? 2. От чего зависит дальность полета тела, брошенного в горизонтальном направлении? По какой траектории движется такое тело? 3. От чего зависит дальность полета тела, брошенного под углом к горизонту? По какой траектории движется такое тело?
4. Под каким углом к горизонту следует бросать с земли мяч, чтобы дальность его полета оказалась максимальной? 5. Как влияет сопротивление воздуха на движение брошенных тел? 6. По какой траектории движется бомба, сброшенная с самолета, относительно: а) Земли; б) самолета?
