Применение первого закона термодинамики к газовым процессам
1. Изопроцессы и адиабатный процесс
Напомним, что согласно первому закону термодинамики количество теплоты Q, переданное газу, связано с изменением внутренней энергии газа ∆U и работой газа Aг соотношением
Q = ∆U + Aг. (1)
Часто требуется применять первый закон термодинамики к газовым процессам, представляющим собой последовательность изопроцессов (иногда добавляется еще адиабатный процесс).
Рассмотрим, как находить величины, фигурирующие в формуле (1), в этих процессах. Напомним, что каждая из тих величин может быть положительной,
Если график газового процесса задан не в координатах (p, V), то желательно начертить график этого же процесса в координатах (p, V), потому что с помощью этого графика легко найти работу газа. Напомним, что работа газа при расширении численно равна площади под графиком зависимости p(V), при сжатии газа — площади под тем же графиком, но взятой о знаком минус.
В большинстве задач на эту тему рассматривается однотомный идеальный газ. Напомним, что его внутренняя энергия выражается формулой
U = (3/2)νRT, (2)
Где ν — количество вещества (число молей), R — универсальная газовая постоянная, T — абсолютная температура.
? 1. Чему равно изменение внутренней энергии газа в изотермическом процессе?
Из формулы (2) и уравнения состояния идеального газа
PV = νRT (3)
Следует, что внутреннюю энергию одноатомного идеального газа можно выразить также формулой
U = (3/2)pV. (4)
С помощью этой формулы можно находить изменение внутренней энергии одноатомного идеального газа, если известны начальные и конечные значения давления и объема газа.
Например, если начальные значения давления и объема обозначить p1 и V1, а конечные — p2 и V2, то
∆U = (3/2) (p2V2 — p1V1). (5)
? 2. Чему равно изменение внутренней энергии при изохорном процессе, если объем газа равен V, а давление изменилось от p1 до p2?
? 3. Чему равно изменение внутренней энергии при изобарном процессе, если давление газа равно p, а объем изменился от V1 до V2?
? 4. На рисунке 47.1 изображен график зависимости p(T) для ν молей одноатомного идеального газа при изохорном переходе из состояния 1 в состояние 2. Даны начальные значения давления и температуры газа p1 и T1, конечная температура T2.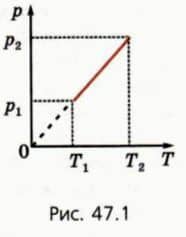 
а) Чему равно конечное давление газа p2? б) Чему равен объем газа V? в) Начертите график этого же процесса в координатах (p, V). г) Чему равна работа газа Aг?
д) Чему равно изменение внутренней энергии ∆U газа? е) Чему равно полученное газом количество теплоты Q?
? 5. На рисунке 47.2 изображен график зависимости V(T), для ν молей одноатомного идеального газа при изобарном переходе из состояния 1 в состояние 2. Даны начальные значения объема и температуры газа V1, и T1, конечная температура T2. 47.2 а) Чему равен конечный объем газа V2? б) Чему равно давление газа p? в) Начертите график этого же процесса в координатах (p, V).
г) Чему равна работа газа Aг? д) Чему равно изменение внутренней энергии газа? е) Чему равно полученное газом количество теплоты Q?
? 6. Используя результаты предыдущих заданий, сравните значения количества теплоты, полученного одним и тем же количеством вещества газа в изохорном и изобарном процессе при нагревании от температуры T1 до температуры T2. а) В каком случае количество теплоты больше? Во сколько раз больше?
б) Объясните этот результат, используя закон сохранения энергии.
Рассмотрим теперь изотермический и адиабатный процессы.
? 7. На рисунке 47.3 приведены графики зависимости p(V) для данной массы газа при изотермическом и адиабатном процессах. Какой график описывает адиабатный процесс? Поясните свой ответ.
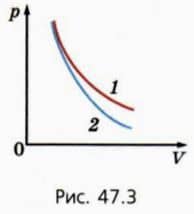
? 8. В каком случае совершенная газом работа больше: когда он расширяется изотермически или адиабатно? Начальные объемы газа одинаковы, конечные объемы тоже одинаковы. Поясните свой ответ.
? 9. Как связаны полученное газом количество теплоты Q и работа газа Aг при изотермическом процессе?
Нахождение работы газа при изотермическом расширении выходит за рамки школьного курса физики. Но в задачах часто используется связь между Q и Aг в изотермическом процессе, выведенная вами при выполнении предыдущего задания.
? 10. В вертикальном цилиндре под поршнем массой 1 кг находится идеальный газ. При изотермическом расширении газа поршень поднялся на 5 см. Примите, что трением между поршнем и стенкой цилиндра можно пренебречь. а) Чему равна работа газа?
б) Чему равно переданное газу количество теплоты?
? 11. Как связаны работа газа Aг и изменение его внутренней энергии ∆U при адиабатном процессе? (Напомним, что при адиабатном процессе отсутствует теплопередача, то есть Q = 0.)
Нахождение работы газа при адиабатном процессе также выходит за рамки школьного курса, но связь между Aг и ∆U в этом процессе широко используется при решении задач.
? 12. При адиабатном расширении 2 молей одноатомного идеального газа газ совершил работу 100 Дж. а) Как изменилась при этом внутренняя энергия газа?
б) Как изменилась температура газа?
2. Циклические процессы
Циклические газовые процессы состоят из нескольких этапов, причем конечное состояние газа совпадает с начальным. Обычно рассматриваются случаи, когда этапами циклического процесса являются изопроцессы и адиабатный процесс.
Вопросы при этом ставятся, например, такие.
- На каких этапах процесса газ получает тепло, а на каких — отдает? Чему равно полученное газом или отданное им количество теплоты? Чему равно изменение внутренней энергии газа на различных этапах процесса? Чему равна работа газа за один цикл? Чему равен КПД цикла?
Для простейшего циклического процесса, состоящего из двух изохор и двух изобар, мы уже нашли ответы на эти вопросы (см. § 43). Рассмотрим теперь более сложный цикл.
На рисунке 47.4 изображен график циклического процесса, происходящего с некоторой массой одноатомного идеального газа.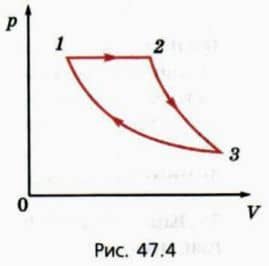 
На этапе 2-3 газ адиабатно расширяется, а на этапе 3-1 изотермически сжимается.
Известно, что при изобарном расширении газ совершает работу A, а при изотермическом сжатии отдает холодильнику количество теплоты Qхол. Требуется найти КПД цикла.
Проанализируем сначала этот циклический процесс качественно. По определению КПД цикла равен отношению работы, совершенной газом за один цикл, к количеству теплоты, переданному газу за этот цикл.
Работа, совершенная газом за один цикл, равна разности работы, совершенной газом при его расширении, и работы, совершенной над газом при его сжатии.
? 13. На каких этапах процесса газ совершает работу, а на каких этапах работу совершают над газом?
? 14. На каких этапах процесса газ получает тепло?
Перейдем теперь к количественному описанию. Заметим, то в подобных задачах как работу газа, так и количество теплоты удобно выражать через число молей газа и значения абсолютной температуры газа в различных состояниях газа, даже если эти значения не заданы (в таком случае они сократятся, если найдено правильное решение).
Обозначим T1, T2 и T3 значения абсолютной температуры соответственно в состояниях 1, 2, 3. Поскольку процесс 3-1 изотермический, T1 = T3.
? 15. Рассмотрим сначала изобарный процесс 1-2. а) Выразите работу газа через давление p в этом процессе и значения объемов газа в состояниях 1 и 2. б) Выразите эту работу через число молей газа и значения абсолютной температуры в состояниях 1 и 2. в) Выразите изменение внутренней энергии газа в процессе 1-2 через число молей газа и значения абсолютной температуры в состояниях 1 и 2. г) Выразите количество теплоты, полученное газом в процессе 1-2, через число молей газа и значения абсолютной температуры в состояниях 1 и 2. д) Как связано переданное газу количество теплоты с работой, совершенной газом?
? 16. Рассмотрим адиабатный процесс 2-3. а) Каково соотношение между работой газа в этом процессе и изменением его внутренней энергии?
б) Выразите работу газа в этом процессе через число молей газа и значения абсолютной температуры в состояниях 2 и 3. в) Найдите соотношение между работой газа в процессе 1-3 и работой газа в процессе 2-3.
? 17. Рассмотрим изотермический процесс 3-1. а) Найдите соотношение между работой газа в этом процессе и количеством теплоты, полученным газом. Учтите, что в данном случае обе эти величины отрицательны.
б) Выразите работу Aвнеш, совершенную в этом процессе над газом, через количество теплоты Qхол, отданное газом холодильнику.
Используя результаты, полученные при выполнении предыдущих заданий, получаем, что работу Aц, совершенную газом за дин цикл, можно выразить через заданные величины: 
3. Расширение газа под поршнем
Трением между поршнем и стенкой сосуда можно пренебречь
Если цилиндрический сосуд с газом расположен вертикально и трением между поршнем и стенками сосуда можно пренебречь, то при медленном нагревании процесс является изобарным. Работа газа
Aг = mgh,
Где m — масса поршня, h — расстояние, на которое поднялся поршень. Используя первый закон термодинамики
Q = ∆U + Aг,
Можно связать перемещение поршня с переданным газу количеством теплоты Q и изменением его внутренней энергии ∆U. Ее можно выразить через изменение температуры ∆T и число молей газа.
? 18. Одноатомный идеальный газ находится в вертикальном цилиндрическом сосуде под поршнем массой 2 кг. Когда газу передали количество теплоты, равное 10 Дж, поршень поднялся на 5 см, а температура газа увеличилась на 2 К. Трением между поршнем и стенкой сосуда можно пренебречь.
Сколько молей газа содержится в сосуде?
Учет трение между поршнем и стенкой сосуда
Типичная ошибка при решении подобных задач состоит в ом, что не учитывают силу трения покоя. Дело в том, что при увеличении давления газа под поршнем он не сдвинется с места до тех пор, пока равнодействующая приложенных к нему сил не превысит максимальную силу трения покоя, которую обычно принимают равной силе трения скольжения. Только поле этого поршень начнет двигаться, и газ начнет расширяться.
Рассмотрим пример. Пусть теперь сосуд расположен горизонтально: в таком случае вес поршня не играет роли.
? 19. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Начальное давление газа равно p0, начальное расстояние от дна сосуда до поршня равно l0, площадь поршня S (рис. 47.5).
При движении поршня на него со стороны стенки сосуда действует сила трения скольжения Fтр. Будем считать, что сосуд находится в вакууме (то есть на поршень не действует сила атмосферного давления).
В начальный момент поршень находится в равновесии. Газу передают некоторое количество теплоты. а) Какое соотношение между p0, Fтр и S следует из условия, что в начальный момент поршень находится в равновесии? б) При каком давлении p газа поршень начнет двигаться?
в) Насколько должна увеличиться внутренняя энергия газа, чтобы поршень начал двигаться? г) Какое количество теплоты Q надо сообщить газу, чтобы поршень начал двигаться? д) Чему будет равно давление p газа, когда поршень будет двигаться равномерно?
е) Какую работу A совершит газ при равномерном перемещении поршня на расстояние d? ж) Насколько увеличится при этом внутренняя энергия газа по сравнению с ее начальным значением? з) Какое количество теплоты Q надо передать газу в начальном состоянии, чтобы поршень сдвинулся на расстояние d?
Дополнительные вопросы и задания
20. На рисунке 47.6 изображен процесс, происходящий с ν молями одноатомного идеального газа.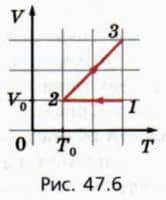 
а) Начертите график этого процесса в координатах (p, V). б) Чему равны работа газа, изменение его внутренней энергии и переданное ему количество теплоты в процессе 1-2? Учтите, что эти значения могут быть отрицательными.
в) Чему равны работа газа, изменение его внутренней энергии и переданное ему количество теплоты в процессе 2-3?
21. На рисунке 47.7 изображен график цикла, происходящего с одноатомным идеальным газом. Найдите КПД цикла.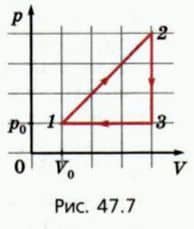 
(3 votes, average: 3,33 out of 5)