Применение уравнения состояния идеального газа
1. Учет гидростатического давления
Сжатие воздуха в сосуде, погруженном в воду
Рассмотрим следующую ситуацию. Пустую открытую стеклянную бутылку опускают в воду на глубину h.
? 1. Объясните, почему при погружении бутылки дном вниз воздух из нее выходит пузырьками и бутылка наполняется водой (рис. 46.1).
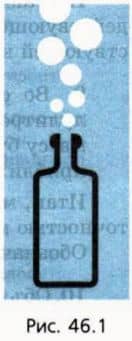
? 2. Почему при этом бутылка сразу тонет?
? 3. Объясните, почему при погружении бутылки дном вверх воздух из нее не выходит (рис. 46.2).
? 4. Объясните, почему
Обозначим плотность воды ρв, внутренний объем бутылки V0, объем содержащегося в ней воздуха Vвозд, атмосферное давление pа. Буем считать, что температура воздуха в бутылке остается постоянной.
? 5. Объясните, почему при погружении бутылки на глубину h справедливо уравнение
Vвозд(pа + ρвgh) = V0pа. (1)
? 6. Во сколько раз уменьшится объем воздуха в бутылке при погружении ее на глубину 10 м?
? 7. Как изменяется действующая на бутылку с воздухом сила Архимеда при увеличении глубины?
? 8. Объясните, почему в данном случае при нахождении силы Архимеда объем погруженного в воду тела надо считать равным суммарному объему стекла и воздуха в бутылке.
При некоторой глубине погружения сила Архимеда станет равной силе тяжести. При погружении на еще большую глубину сила Архимеда будет уже меньше силы тяжести, поэтому бутылка с воздухом начнет тонуть.
Поставим вопрос: можно ли пренебречь силой тяжести, действующей на воздух, по сравнению с силой тяжести, действующей на бутылку?
? 9. Во сколько раз масса воздуха, содержащегося в полулитровой бутылке, меньше массы бутылки? Примите массу бутылки равной 0,5 кг; плотность воздуха при 20 ºС приближенно равна 1,2 кг/м3.
Итак, мы видим, что массой воздуха в бутылке с хорошей точностью можно пренебречь по сравнению с массой бутылки.
Обозначим плотность стекла ρс, а объем стекла Vс.
? 10. Объясните, почему, когда погруженная полностью в воду бутылка с воздухом находится в равновесии, справедливо следующее уравнение:
ΡсVсg = ρвg(Vвозд + Vс). (2)
Уравнения (1) и (2) можно рассматривать как систему двух уравнений с двумя неизвестными. Например, если известны значения всех входящих в эти уравнения величин, кроме Vвозд и h, их можно найти с помощью этих уравнений.
? 11. В воду опускают дном вверх открытую бутылку, содержащую воздух при атмосферном давлении. Вместимость бутылки 0,5 л, объем стекла 0,2 л, плотность стекла в 2,5 раза больше плотности воды, атмосферное давление 100 кПа. а) Чему равен объем воздуха в бутылке, когда погруженная в воду бутылка находится в равновесии?
б) На какой глубине будет при этом бутылка?
В рассмотренной ситуации массой воздуха можно пренебречь, потому что при давлении, близком к атмосферному, плотность воздуха намного меньше плотности воды и твердых тел.
Но в случаях, когда речь идет о поднятии грузов с большой глубины с помощью сжатого воздуха, масса сжатого воздуха может оказаться существенной.
Рассмотрим пример.
? 12. Исследователи океанских глубин обнаружили на глубине 1 км затонувший сундук с сокровищами. Масса сундука 2,5 т, объем — 1 м3.
Сундук привязали тросом к прочному пустому водонепроницаемому мешку и стали закачивать в мешок воздух до тех пор, пока он не начал всплывать вместе с сундуком. Для упрощения расчетов примем плотность морской воды равной плотности пресной воды, Будем считать воду несжимаемой, а объем оболочки мешка пренебрежимо малым. Температуру воды на большой глубине можно считать близкой к 0 ºС.
а) Надо ли учитывать атмосферное давление для определения давления воздуха в мешке? б) Обозначим ρ плотность воды, mс и mв массу сундука и массу воздуха в мешке, Vс и Vв объем сундука и объем воздуха в начале всплытия, Mв — молярную массу воздуха, T — абсолютную температуру воды. Запишите систему двух уравнений с двумя неизвестными (mв и Vв), считая, что атмосферным давлением можно пренебречь. в) Чему равен объем воздуха в мешке в тот момент, когда мешок с сундуком начал всплывать? г) Чему равна масса воздуха в мешке, когда мешок с сундуком начал всплывать?
д) Можно ли не выпускать из мешка воздух до тех пор, пока мешок с сундуком не всплывут на поверхность?
Воздух в трубке с ртутным столбиком
В стеклянной трубке, запаянной с одного конца, находится воздух. Этот воздух отделен от атмосферного воздуха столбиком ртути длиной lрт (рис. 46.3). 
Рассмотрим, как зависит длина заполненной воздухом части трубки от положения трубки и температуры воздуха в ней. Будем считать, что длина трубки достаточно велика для того, чтобы ртуть не выливалась из трубки при любом ее положении.
Обозначим атмосферное давление pа, плотность ртути ρрт, а длину заполненной воздухом части трубки, когда она расположена горизонтально, обозначим l0. Примем сначала, что температура воздуха в трубке постоянна.
? 13. Запишите уравнение, которое связывает величины lрт, l0 и длину l заполненной воздухом части трубки, когда она расположена: а) вертикально открытым концом вверх; б) вертикально открытым концом вниз.
? 14. В начальный момент трубка расположена открытым концом вниз. Когда ее перевернули открытым концом вверх, длина заполненной воздухом части трубки уменьшилась на 10 %. Чему равна длина столбика ртути, если атмосферное давление равно 760 мм рт. ст.?
Рассмотрим теперь случай, когда температура воздуха в рубке изменяется.
? 15. В начальный момент трубка с воздухом и столбиком ртути расположена горизонтально. Когда ее опустили в кипяток открытым концом вверх, длина заполненной воздухом части трубки увеличилась на 20 %. Чему равна начальная температура воздуха в трубке, если длина столбика ртути равна 5 см? Атмосферное давление равно 760 мм рт. ст. Подсказка.
Воспользуйтесь уравнением состояния идеального газа.
2. Два газа в цилиндре с поршнем или перегородкой
Цилиндр расположен горизонтально
Рассмотрим сначала случай, когда цилиндр с различными газами расположен горизонтально (на рисунке 46.4 различные газы схематически обозначены разными цветами). В таком случае можно не учитывать вес поршня. 
Поршень может обладать различными свойствами, которые обязательно надо учитывать при решении задач.
? 16. Что можно сказать о давлении и температуре двух газов, разделенных поршнем, если он: а) теплопроводящий и может двигаться без трения? б) не проводит тепло, но может двигаться без трения?
в) теплопроводящий, но надо учитывать трение между поршнем и стенками сосуда?
? 17. В горизонтально расположенном цилиндре с поршнем по разные стороны от поршня находятся водород и кислород. а) Каким соотношением связаны объемы газов и количества вещества в них, если поршень подвижный и теплопроводящий? б) Каким соотношением связаны объемы и массы газов в этом случае?
в) Как связаны объемы, массы и температуры газов, если поршень подвижный, но не проводит тепло?
Если сказано, что сосуд разделен не поршнем, а перегородкой, то подразумевается, что объемы частей сосуда остаются постоянными. Перегородка тоже может обладать различными свойствами.
? 18. Что можно сказать о температуре и парциальном давлении двух газов, разделенных перегородкой, если она: а) теплопроводящая? б) пористая (это обычно означает, что молекулы одного газа могут проникать сквозь перегородку, а молекулы другого газа не могут)?
? 19. Теплоизолированный сосуд разделен пористой перегородкой на две равные части. В начальный момент в левой части сосуда находится 2 моль гелия, а в правой — 1 моль аргона.
Начальная температура гелия 300 К, а начальная температура аргона 600 К. Атомы гелия могут свободно проникать через поры в перегородке, а атомы аргона не могут. а) Имеет ли значение, проводит перегородка тепло или нет? б) Атомы какого газа в начальный момент обладают большей средней кинетической энергией? Во сколько раз большей? в) Внутренняя энергия какого газа в начальный момент больше?
Во сколько раз больше? г) Объясните, почему средние кинетические энергии атомов различных газов равны после достижения теплового равновесия. д) Какая температура будет в сосуде при тепловом равновесии?
е) Во сколько раз средняя кинетическая энергия атомов гелия при тепловом равновесии будет больше их средней кинетической энергии в начальном состоянии? ж) Как изменится давление гелия в левой части сосуда по сравнению с начальным после установления равновесия? з) Как изменится давление аргона по сравнению с начальным после установления равновесия?
и) Давление в какой части сосуда будет больше после установления равновесия? Во сколько раз больше?
Цилиндр расположен вертикально
Если цилиндр расположен вертикально (рис. 46.5), то надо учитывать вес поршня, который давит на газ, находящийся в нижней части цилиндра. Из-за этого давление в нижней части цилиндра больше, чем в верхней.
Рассмотрим пример. 
? 20. Вертикально расположенный цилиндрический сосуд высотой l разделен подвижным поршнем на две части. В верхней части высотой lв находится ν молей гелия, а в нижней части высотой lн — столько же молей водорода. Температура газов остается все время равной T. Масса поршня m, площадь S, толщиной поршня можно пренебречь по сравнению с высотой сосуда.
а) Выразите давление в каждой части сосуда через другие величины. Имеет ли для этого значение вид газа в частях сосуда? б) Напишите уравнение, связывающее давления газов в каждой части сосуда с массой поршня и его площадью. в) Чему равна масса поршня, если l = 50 см, ν = 0,22 моль, T = 361 К, lв = 30 см? Подсказка.
Воспользуйтесь уравнением состояния идеального газа.
Подъемная сила воздушного шара
Воздушный шар (рис. 46.6) может находиться в воздухе в равновесии только при условии, что действующая на него со стороны воздуха сила Архимеда равна по модулю суммарной силе тяжести, действующей на шар и подвешенный к нему груз:
FА = Fт. ш + Fт. гр. (3)
В случае воздушного шара ила Архимеда равна весу окружающего воздуха в объеме, занятом шаром и грузом. Мы выделили слово «окружающего» курсивом, потому что плотность атмосферного воздуха при подъеме изменяется по двум причинам: во-первых, уменьшается его давление, во-вторых, понижается его температура.
Обозначим объем шара V. Объемом груза и оболочки шара обычно пренебрегают по сравнению с объемом самого шара, но массы груза и оболочки шара имеют большое значение! Массу груза обозначим mгр, а массу оболочки — mоб. Тогда
Fт. ш = (mвнутр + mоб)g,
Где mвнутр — масса газа, которым наполнен шар.
Обозначим плотность окружающего шар воздуха ρвнеш, а плотность газа, находящегося внутри шара, ρвнутр.
? 21. Объясните, почему справедливы следующие уравнения:
FА = ρвнешgV, mвнутр = ρвнутрV, V(ρвнеш — ρвнутр) = mгр + mоб. (4)
Подсказка. Воспользуйтесь уравнением (3) и соотношением между массой, объемом и плотностью.
Подземной силой воздушного шара называют вес груза, который может поднять этот шар.
? 22. Объясните, почему модуль подъемной силы воздушного шара выражается формулой
Fпод = Vg(ρвнеш — ρвнутр) — mобg. (5)
Из формул (4) и (5) следует, что воздушный шар может поднять груз только при условии, что плотность газа, которым наполнен шар, меньше плотности окружающего воздуха.
Если бы шар был жестким, этого можно было бы достичь, частично выкачав из него воздух: жесткая оболочка смогла бы выдержать разность давлений воздуха внутри и вне шара. Однако оболочка жесткого шара была бы слишком тяжелой. Мягкая же оболочка, которую всегда используют для воздушных шаров, не может выдержать сколько-нибудь значительной разности давлений.
Поэтому давление газа внутри шара равно давлению окружающего воздуха.
? 23. Объясните, почему если давление внутри шара равно давлению окружающего воздуха, то справедливо равенство
Ρвнутр/ρвнеш = (Mвнутр * Tвнеш) / (Mвнеш * Tвнутр). (6)
Подсказка. Воспользуйтесь уравнением состояния идеального газа.
Из формулы (6) видно, что плотность газа, которым наполняют шар, можно сделать меньше плотности окружающего воздуха двумя способами: — использовать в качестве «внутреннего» газа нагретый воздух; — использовать газ с меньшей молярной массой.
Первый способ используют для прогулочных воздушных шаров (рис. 46.6), а второй — для метеорологических зондов (рис. 46.7), которые поднимаются на большую высоту (в таком случае шар наполняют обычно гелием).
? 24. Объясните, почему из формул (5) и (6) следует, что модуль подъемной силы воздушного шара выражается формулой
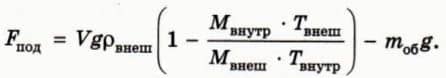? 25. Воздушный шар объемом 3000 м3 имеет в нижней части отверстие, через которое воздух внутри шара нагревается горелкой до температуры 77 ºС. Шар находится в равновесии на высоте, где температура окружающего воздуха равна 7 ºС, а его плотность равна 1,2 кг/м3.
Масса оболочки шара 300 кг. Чему равна масса груза?
Дополнительные вопросы и задания
26. В понтон, лежащий на дне озера на глубине 90 м, закачивают сверху воздух (рис. 46.8). При атом вода вытесняется из понтона через отверстие, расположенное в нижней его части. Какой объем атмосферного воздуха надо подать в понтон, чтобы он мог поднять груз, если суммарная масса понтона с грузом равна 20 т, а суммарный объем груза и стенок понтона равен 5 м3?
Примите, что температура воды близка к 0 ºС, а атмосферное давление равно 105 Па.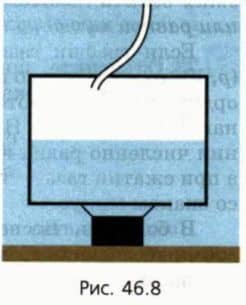 
27. В запаянном колене U-образной трубки находится столб воздуха высотой 30 см. Ртуть в обоих коленах находится на одном уровне. Какой станет высота столба воздуха, если медленно долить ртуть доверху?
Давление равно нормальному атмосферному давлению.
28. Наполненный гелием шар находится в равновесии в воздухе. Масса одного квадратного метра оболочки шара равна 50 г, температура воздуха и гелия 27 ºС, давление равно нормальному атмосферному давлению. Чему равен радиус шара?
(1 votes, average: 5,00 out of 5)