Работа в термодинамике
Работа в механике и термодинамике. В механике работа определяется как произведение модулей силы и перемещения, умноженное на косинус угла между ними. Работа совершается при действии силы на движущееся тело и равна изменению кинетической энергии тела.
В термодинамике движение тела как целого не рассматривается и речь идет о перемещении частей макроскопического тела друг относительно друга. В результате меняется объем тела, а его скорость остается равной нулю. Следовательно, работа в термодинамике, определяемая так же, как и в механике,
Изменение внутренней энергии при совершении работы. Почему при сжатии или расширении меняется внутренняя энергия тела? Почему, в частности, нагревается воздух при накачивании велосипедной шины?
Причина изменения температуры в процессе сжатия газа состоит в следующем: при упругих соударениях молекул с движущимся поршнем их кинетическая энергия изменяется. При движении навстречу молекулам поршень передает им во время столкновений часть своей механической энергии, в результате чего газ нагревается. Поршень действует подобно футболисту, встречающему летящий мяч ударом ноги и сообщающему мячу скорость, значительно большую той, которой он обладал до удара.
Если газ, напротив, расширяется, то после столкновения с удаляющимся поршнем скорости молекул уменьшаются, в результате чего газ охлаждается. Так же действует футболист, для того чтобы уменьшить скорость летящего мяча или остановить его; нога футболиста движется от мяча, как бы уступая ему дорогу.
При сжатии или расширении меняется и средняя потенциальная энергия взаимодействия молекул, так как при этом меняется среднее расстояние между молекулами.
Вычисление работы. Вычислим работу в зависимости от изменения объема на примере газа в цилиндре под поршнем (рис. 39).
Проще всего вначале вычислить не работу силы F, действующей на газ со стороны внешнего тела (поршня), а работу, которую совершает сам газ, действуя на поршень с силой F’. Согласно третьему закону Ньютона F’ = — F.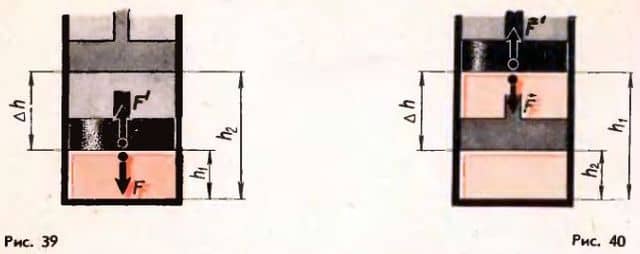 
Модуль силы, действующей со стороны газа на поршень, равен: F’ = pS, где p — давление газа, а S — площадь поршня. Пусть газ расширяется и поршень смещается в направлении силы F’ на малое расстояние ∆h = h2 — h1.
Если перемещение мало, то давление газа можно считать постоянным.
Работа газа равна:
A’ = F’∆h = pS(h2 — h1) = p(Sh2 — Sh1). (4.2)
Эту работу можно выразить через изменение объема газа. Начальный объем V1 = Sh1, а конечный V2 = Sh2. Поэтому
A’ = p(V2 — V1) = p∆V, (4.3)
Где ∆V = V2 — V1 — изменение объема газа.
При расширении газ совершает положительную работу, так как направление силы и направление перемещения поршня совпадают. В процессе расширения газ передает энергию окружающим телам.
Если газ сжимается, то формула (4.3) для работы газа остается справедливой. Но теперь V21 и поэтому A’
Работа A, совершаемая внешними телами над газом, отличается от работы газа A’ только знаком: A = — A’, так как сила F, действующая на газ, направлена против силы F’, а перемещение остается тем же самым. Поэтому работа внешних сил, действующих на газ, равна:
A = — A’ = — p∆V (4.4)
Знак минус указывает, что при сжатии газа, когда ∆V = V2 — V1 0: при сжатии газа направления силы и перемещения совпадают. Совершая над газом положительную работу, внешние тела передают ему энергию. При расширении газа, наоборот, работа внешних тел отрицательна (A 2 — V1 > 0. Теперь направления силы и перемещения противоположны.
Выражения (4.3) и (4.4) справедливы не только при сжатии или расширении газа в цилиндре, но и при малом изменении объема любой системы. Если процесс изобарный (p = const), то эти формулы можно применять и для больших изменений объема.
Геометрическое истолкование работы. Работе A’ газа для случая постоянного давления можно дать простое геометрическое истолкование.
Построим график зависимости давления газа от объема (рис. 41) . Здесь площадь прямоугольника abcd, ограниченная графиком p1 = const, осью V и отрезками ab и cd, равными давлению газа, численно равна работе (4.3).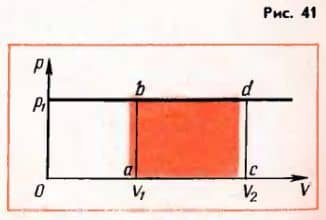 
В общем случае при произвольном изменении объема газа давление не остается неизменным. Например, при изотермическом процессе оно убывает обратно пропорционально объему (рис. 42).
В этом случае для вычисления работы нужно разделить общее изменение объема на малые части, вычислить элементарные (малые) работы, а потом все их сложить. Работа газа по-прежнему будет численно равна площади фигуры, ограниченной графиком зависимости p от V, осью V и отрезками ab и cd, равными давлениям p1, p2 в начальном и конечном состояниях.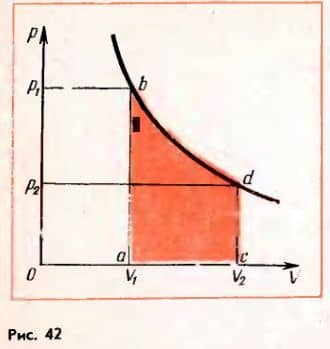 
1. От каких физических величин зависит внутренняя энергия тела? 2. Приведите примеры превращения механической энергии во внутреннюю и обратно в темнике и быту. 3. Чему равна внутренняя энергия идеального одноатомного газа? 4. Моль какого газа — водорода или гелия — имеет большую внутреннюю энергию при одинаковой температуре газов?
5. Почему газ при сжатии нагревается? 6. Чему равна работа, совершаемая внешними силами при сжатии и расширении тел?
(2 votes, average: 3,00 out of 5)