Движение системы тел
1. Гладкая горка и шайба
Горка с одной вершиной
Пусть на гладком столе покоится гладкая горка массой M и высотой H (рис. 34.1). На нее налетает со скоростью 
0 шайба массой m. Двигаясь по горке, шайба не отрывается от нее.
Возможны три варианта развития событий.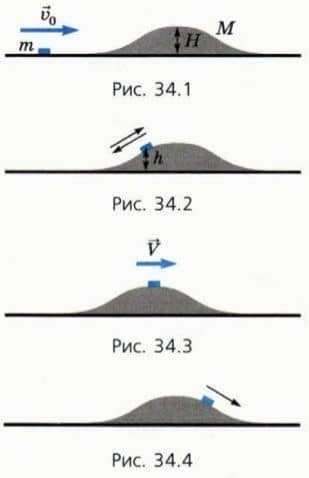 
1) Шайба не достигнет вершины горки и соскользнет по тому же склону (рис. 34.2).
2) Шайба достигнет вершины горки в момент, когда их скорости относительно стола равны (рис. 34.3).
3) Шайба «перевалит» через
Второй вариант — «пограничный». Поэтому с него и начнем: выясним, при каких значениях M, H, m, v0 он реализуется.
? 1. Объясните, почему в случае, когда горка и шайба в результате взаимодействия движутся как единое целое со скоростью V, справедливы уравнения
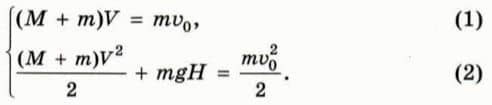
? 2. Выразите общую скорость горки и шайбы V через M, H, m. Подсказка.
Используя уравнение (1), выразите v0 через M, m, V и подставьте в уравнение (2).
? 3. Используя полученную при выполнении предыдущего задания формулу, объясните, почему общая скорость горки и шайбы стремится к нулю, когда масса шайбы намного меньше массы горки.
? 4. На покоящуюся гладкую горку массой M и высотой H налетает шайба массой m со скоростью 0. В результате взаимодействия горка и шайба стали двигаться как единое целое. а) Чему равна начальная скорость шайбы, если M = 1 кг, m = 100 г, H = 20 см?
б) Чему равна высота горки, если v0 = 3 м/с, а масса шайбы в 2 раза меньше массы горки? в) Чему равна масса шайбы, если v0 = 1 м/с, M = 2 кг, H = 4 см?
Рассмотрим теперь кратко оставшиеся варианты.
Пусть реализуется первый вариант: шайба не достигла вершины горки и соскользнула обратно, см. рисунок 34.2. В таком случае для нахождения значений конечной скорости горки и шайбы их можно рассматривать как тела, между которыми произошло упругое столкновение (см. § 32).
Действительно, в конечном состоянии шайба снова скользит по столу, поэтому ее потенциальная энергия не изменилась по сравнению с начальной. Следовательно, сохранилась и суммарная кинетическая энергия горки и шайбы. Кроме того, сохранился и их суммарный импульс.
Начальную скорость шайбы можно найти, зная максимальную высоту, до которой она поднялась по горке.
? 5. На покоящуюся гладкую горку массой 1 кг и высотой 15 см налетает слева шайба массой 300 г. Шайба достигает максимальной высоты 10 см. а) Какова начальная скорость шайбы? б) Чему равна общая скорость горки и шайбы в момент, когда шайба остановится относительно горки? в) Чему равны конечные скорости горки и шайбы и как они направлены? Подсказка.
В момент, когда шайба достигла максимальной высоты, ее скорость относительно стола равна скорости горки и направлена горизонтально.
Рассмотрим наконец третий вариант, когда шайба преодолевает горку и скользит по столу дальше.
? 6. Объясните, почему в этом случае конечная скорость шайбы равна ее начальной скорости, а конечная скорость горки равна нулю. Подсказка. Это — единственное решение системы уравнений, выражающих законы сохранения энергии и импульса, если шайба в конечном состоянии находится по другую сторону горки.
Итак, поднимаясь на горку, шайба разгоняет ее, а спускаясь по другому склону, тормозит горку до остановки.
Горка с двумя вершинами
Возьмем теперь гладкую горку массой M с двумя вершинами высотой H и h (рис. 34.5). На более высокой из них в начальном состоянии покоится шайба массой m. Шайба начинает соскальзывать влево. При движении тел шайба не отрывалась от горки, а горка — от гладкого стола.
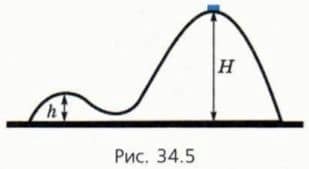
? 7. Какие физические величины сохраняются в данном случае?
? 8. Запишите систему уравнений, выражающую законы сохранения, для момента, когда шайба будет на вершине высотой h. Какие величины можно найти с помощью этой системы? Выразите эти величины через приведенные выше.
? 9. Чему равны скорости горки и шайбы, когда шайба находится на второй вершине горки, если M = 100 г, m = 20 г, H = 8 см, h = 2 см (см. рис. 34.5)? Как будут направлены эти скорости?
Движение шайбы в бруске со сферической выемкой
Рассмотрим теперь случай, когда шайба движется во впадине между двумя вершинами гладкой горки. Такую «горку» представляют иногда как брусок с выемкой.
Пусть на гладком столе покоится брусок массой M с гладкой выемкой глубиной H. На левый край выемки осторожно кладут шайбу массой m и без толчка отпускают (рис. 34.6).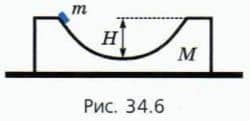 
? 10. Какие физические величины сохраняются в данном случае?
? 11. Запишите систему уравнений, выражающую законы сохранения для момента, когда шайба проходит дно выемки.
? 12. Чему равно отношение массы шайбы к массе бруска, если максимальная скорость шайбы относительно стола равна 1,9 м/с, а глубина выемки равна 20 см?
Пусть теперь брусок находится у стены (рис. 34.7). Тогда движение тел удобно разделить на три этапа.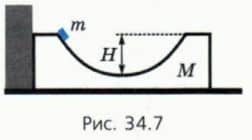 
1. Спуск шайбы. При этом шайба давит на брусок силой, которая имеет горизонтальную составляющую, правленную влево. Но брусок не может двигаться влево, потому что упирается в стену.
Стенка при этом давит на брусок, поэтому горизонтальная проекция суммарного импульса бруска и шайбы не сохраняется. Но сохраняется механическая энергия шайбы.
2. Подъем шайбы. Поднимаясь по правой стороне выемки, шайба давит на брусок силой, которая имеет горизонтальную составляющую, направленную вправо, поэтому он начнет скользить по столу вправо. Теперь горизонтальная проекция суммарного импульса бруска и шайбы сохраняется.
Их суммарная механическая энергия также сохраняется.
3. Момент, когда шайба поднялась на максимально возможную высоту h по правой стороне выемки (рис. 34.8). Достигнув высоты h, шайба на мгновенье останавливается относительно бруска, поэтому их скорости относительно стола будут равны и направлены горизонтально. Заметим, что h < H, поскольку часть своей механической энергии шайба передала бруску.
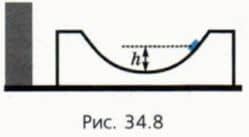
? 13. Шайба начала соскальзывать с высоты H (см. рис. 34.7) и приобрела скорость v относительно стола, когда оказалась на дне выемки.
Обозначим V общую скорость шайбы и бруска в момент, когда шайба поднялась на максимально возможную высоту h по правой стороне выемки. Объясните почему справедливы следующие уравнения:
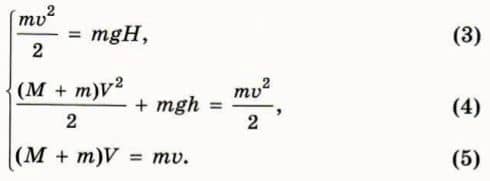
? 14. Выразите h через H, M, m. Подсказка. Воспользуйтесь уравнением (5), чтобы выразить V через v, M, m, и подставьте полученное выражение в (4).
Получится система двух уравнений с двумя неизвестными (h и v).
? 15. У стены на гладком столе покоится брусок массой 400 г с выемкой глубиной 15 см (см. рис. 34.7).
На левый край выемки кладут шайбу и отпускают без толчка. Шайба поднимается по правой стороне выемки на высоту 10 см. Чему равна масса шайбы?
2. Системы с пружиной
Пусть на гладком столе лежит груз массой M, к которому прикреплена пружина жесткостью k (рис. 34.9). На эту систему налетает со скоростью 0 брусок массой m.
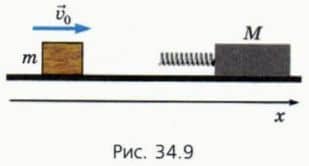
? 16. Каковы проекции конечных скоростей груза и бруска на ось x, изображенную на рисунке 34.9? Подсказка. Для нахождения конечных скоростей груз и брусок можно рассматривать как тела, между которыми произошло упругое столкновение (см. § 32).
Для ответа на этот вопрос не нужна жесткость пружины.
Деформация пружины максимальна в тот момент, когда брусок н груз сблизились на минимальное расстояние. При этом их скорости относительно стола равны. Обозначим xmax модуль деформации пружины, а V — общую скорость бруска и груза в этот момент.
? 17. Объясните, почему для этого момента справедливы следующие уравнения:
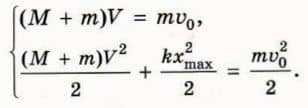
? 18. Чему равен модуль максимальной деформации пружины, если M = 1 кг, m = 300 г, k = 500 Н/м, v0 = 2 м/с?
Рассмотрим теперь случай, когда надо учитывать трение. Пусть на столе покоятся небольшие бруски массой m1 и m2 (рис. 34.10). Между ними находится сжатая пружина жесткостью k, которая удерживается нитью в деформированном состоянии.
Модуль деформации пружины равен x. Коэффициент трения между брусками и столом равен μ. Когда нить пережгли, бруски разъехались на расстояние l друг от друга. Будем считать, что размерами брусков и пружины можно пренебречь по сравнению с l.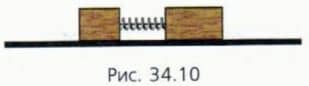 
? 19. Чему равны: а) начальная механическая энергия системы? б) конечная механическая энергия этой системы?
в) работа силы трения скольжения?
? 20. Чему равен коэффициент трения μ, если m1 = 200 г, m2 = 300 г, k = 500 Н/м, x = 5 см, l = 50 см?
Дополнительные вопросы и задания
21. Человек массой m стоит на одном конце покоящейся на рельсах тележки длиной L и массой M (рис. 34.11). Он начинает идти с постоянной скоростью vчт относительно тележки и останавливается (относительно тележки) у другого ее конца.
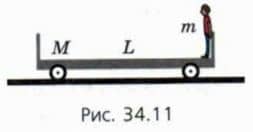а) Чему равно отношение модулей скорости человека и тележки относительно рельсов vчр/vтр? б) Как выражается vчт через vчр и vтр? в) Чему равно vтр? г) Чему равно vчр? д) Сколько времени человек будет идти от одного конца тележки до другого?
е) Насколько переместится тележка за время, пока человек движется от одного ее конца до другого? ж) Чему будет равна скорость тележки, когда человек остановится у другого ее конца?
22. На тележке укреплен поднес, к которому на нити длиной l подвешен шарик массой m (рис. 34.12). Масса тележки с подвесом равна M. Шарик отклоняют, как показано на рисунке, и отпускают без толчка. Сопротивлением воздуха и трением можно пренебречь.
Обозначим v и V модули скорости шарика и тележки в момент, когда шарик проходит положение равновесия. За нулевой уровень потенциальной энергии шарика примем его положение равновесия.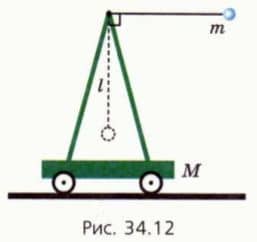 
а) Чему равна начальная механическая энергия системы «тележка + шарик»?
б) Чему равна кинетическая энергия этой системы в момент, когда шарик проходит положение равновесия? в) Чему равны в этот момент модули скорости шарика и тележки относительно стола, если M = 200 г, m = 50 г, l = 30 см?
23. На гладком столе покоятся два бруска массой 2 кг и 3 кг, соединенные пружиной жесткостью 10 кН/м (рис. 34.13). В левый брусок (массой 2 кг) попадает и застревает в нем пуля массой 10 г, летящая горизонтально со скоростью 600 м/с. 
а) Чему равна скорость бруска сразу после столкновения с пулей?
б) Чему равны скорости брусков в момент, когда деформация пружины максимальна? в) Чему равен модуль максимальной деформации пружины? 
(1 votes, average: 5,00 out of 5)