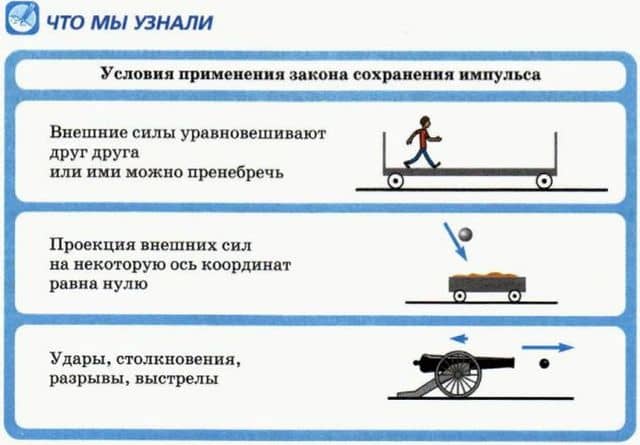
Условия применения закона сохранения импульса
Как мы уже говорили, в точности замкнутых систем тел не существует. Поэтому возникает вопрос: в каких случаях можно применять закон сохранения импульса к незамкнутым системам тел? Рассмотрим эти случаи.
1. Внешние силы уравновешивают друг друга или ими можно пренебречь
С этим случаем мы уже познакомились в предыдущем параграфе на примере двух взаимодействующих тележек.
В качестве второго примера вспомним первоклассника и десятиклассника, соревнующихся в перетягивании каната, стоя на скейтбордах (рис. 26.1). При этом внешние силы
Поэтому сумма импульсов соперников сохраняется.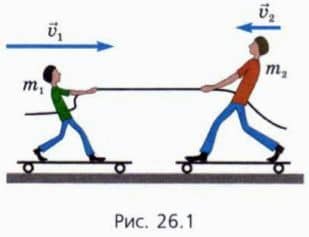 
Пусть в начальный момент школьники покоились. Тогда их суммарный импульс в начальный момент равен нулю. Согласно закону сохранения импульса он останется равным нулю и тогда, когда они будут двигаться.
Следовательно, 
где 
1 и 2 — скорости школьников в произвольный момент (пока действия всех других тел компенсируются).
? 1. Докажите, что отношение модулей скоростей мальчиков обратно отношению их масс:
V1/v2 = m2/m1. (2)
Обратите внимание: это соотношение будет выполняться независимо от того, как взаимодействуют соперники. Например, не имеет значения, тянут они канат рывками или плавно, перебирает канат руками только кто-то один из них или оба.
? 2. На рельсах стоит платформа массой 120 кг, а на ней — человек массой 60 кг (рис. 26.2, а). Трением между колесами платформы и рельсами можно пренебречь. Человек начинает идти вдоль платформы вправо со скоростью 1,2 м/с относительно платформы (рис.
26.2, б).
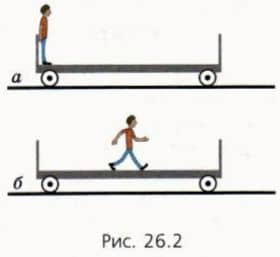
Начальный суммарный импульс платформы и человека равен нулю в системе отсчета, связанной с землей. Поэтому применим закон сохранения импульса в этой системе отсчета.
А) Чему равно отношение скорости человека к скорости платформы относительно земли? б) Как связаны модули скорости человека относительно платформы, скорости человека относительно земли и скорости платформы относительно земли? в) С какой скоростью и в каком направлении будет двигаться платформа относительно земли?
г) Чему будут равны скорости человека и платформы относительно земли, когда он дойдет до ее противоположного конца и остановится?
2. Проекция внешних сил на некоторую ось координат равна нулю
Пусть, например, по рельсам со скоростью катится тележка с песком массой mт. Будем считать, что трением между колесами тележки и рельсами можно пренебречь.
В тележку падает груз массой mг (рис. 26.3, а), и тележка катится далее с грузом (рис. 26.3, б).
Обозначим конечную скорость тележки с грузом К.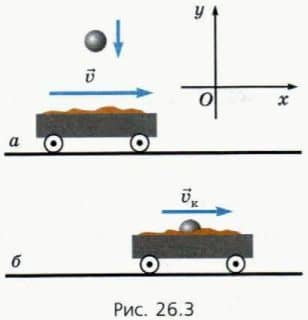 
Введем оси координат, как показано на рисунке. На тела действовали только вертикально направленные внешние силы (сила тяжести и сила нормальной реакции со стороны рельсов). Эти силы не могут изменить горизонтальные проекции импульсов тел.
Поэтому проекция суммарного импульса тел на горизонтально направленную ось х осталась неизменной.
? 3. Докажите, что конечная скорость тележки с грузом
Vк = v(mт/(mт + mг)).
Мы видим, что скорость тележки после падения груза уменьшилась.
Уменьшение скорости тележки объясняется тем, что часть своего начального горизонтально направленного импульса она передала грузу, разгоняя его до скорости К. Когда тележка разгоняла груз, он, согласно третьему закону Ньютона, тормозил тележку.
Обратите внимание на то, что в рассматриваемом процессе суммарный импульс тележки и груза не сохранялся. Неизменной осталась лишь проекция суммарного импульса тел на горизонтально направленную ось x.
Проекция же суммарного импульса тел на вертикально направленную ось у в данном процессе изменилась: перед падением груза она была отлична от нуля (груз двигался вниз), а после падения груза она стала равной нулю (оба тела движутся горизонтально).
? 4. В стоящую на рельсах тележку с песком массой 20 кг влетает груз массой 10 кг. Скорость груза непосредственно перед попаданием в тележку равна 6 м/с и направлена под углом 60º к горизонту (рис. 26.4).
Трением между колесами тележки и рельсами можно пренебречь.
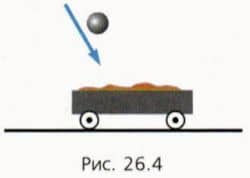а) Какая проекция суммарного импульса в данном случае сохраняется? б) Чему равна горизонтальная проекция импульса груза непосредственно перед его попаданием в тележку? в) С какой скоростью будет двигаться тележка с грузом?
3. Удары, столкновения, разрывы, выстрелы
В этих случаях происходит значительное изменение скорости тел (а значит, и их импульса) за очень краткий промежуток времени. Как мы уже знаем (см. предыдущий параграф), это означает, что в течение этого промежутка времени тела действуют друг на друга с большими силами. Обычно эти силы намного превышают внешние силы, действующие на тела системы.
Поэтому систему тел во время таких взаимодействий можно с хорошей степенью точности считать замкнутой, благодаря чему можно использовать закон сохранения импульса.
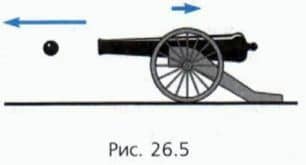
Например, когда во время пушечного выстрела ядро движется внутри ствола пушки, силы, с которыми действуют друг на друга пушка и ядро, намного превышают горизонтально направленные внешние силы, действующие на эти тела.
? 5. Из пушки массой 200 кг выстрелили в горизонтальном направлении ядром массой 10 кг (рис. 26.5). Ядро вылетело из пушки со скоростью 200 м/с.
Какова скорость пушки при отдаче?
При столкновениях тела также действуют друг на друга с довольно большими силами в течение краткого промежутка времени.
Наиболее простым для изучения является так называемое абсолютно неупругое столкновение (или абсолютно неупругий удар). Так называют столкновение тел, в результате которого они начинают двигаться как единое целое. Именно так взаимодействовали тележки в первом опыте (см. рис.
25.1), рассмотренном в предыдущем параграфе, Найти общую скорость тел после абсолютно неупругого столкновения довольно просто.
? 6. Два пластилиновых шарика массой m1 и m2 движутся со скоростями 1 и 2. В результате столкновения они стали двигаться как единое целое. Докажите, что их общую скорость можно найти с помощью формулы
Обычно рассматривают случаи, когда тела до столкновения движутся вдоль одной прямой. Направим ось x вдоль этой прямой. Тогда в проекциях на эту ось формула (3) принимает вид
Направление общей скорости тел после абсолютно неупругого столкновения определяется знаком проекции vx.
? 7. Объясните, почему из формулы (4) следует, что скорость «объединенного тела» будет направлена так же, как начальная скорость тела с большим импульсом.
? 8. Две тележки движутся навстречу друг другу. При столкновении они сцепляются и движутся как единое целое. Обозначим массу и скорость тележки, которая вначале ехала вправо, mп и П, а массу и скорость тележки, которая вначале ехала влево, mл и Л. В каком направлении и с какой скоростью будут двигаться сцепленные тележки, если: а) mп = 1 кг, vп = 2 м/с, mл = 2 кг, vл = 0,5 м/с?
б) mп = 1 кг, vп = 2 м/с, mл = 4 кг, vл = 0,5 м/с? в) mп = 1 кг, vп = 2 м/с, mл = 0,5 кг, vл = 6 м/с?
Дополнительные вопросы и задания
В заданиях к этому параграфу предполагается, что трением можно пренебречь (если не указан коэффициент трения).
9. На рельсах стоит тележка массой 100 кг. Бегущий вдоль рельсов школьник массой 50 кг с разбега запрыгнул на эту тележку, после чего она вместе со школьником стала двигаться со скоростью 2 м/с. Чему была равна скорость школьника непосредственно перед прыжком?
10. На рельсах недалеко друг от друга стоят две тележки массой M каждая. На первой из них стоит человек массой m. Человек перепрыгивает с первой тележки на вторую. а) Скорость какой тележки будет больше?
б) Чему будет равно отношение скоростей тележек?
11. Из зенитного орудия, установленного на железнодорожной платформе, производят выстрел снарядом массой m под углом α к горизонту. Начальная скорость снаряда v0. Какую скорость приобретет платформа, если ее масса вместе с орудием равна M? В начальный момент платформа покоилась.
12. Скользящая по льду шайба массой 160 г ударяется о лежащую льдинку. После удара шайба скользит в прежнем направлении, но модуль ее скорости уменьшился вдвое. Скорость же льдинки стала равной начальной скорости шайбы.
Чему равна масса льдинки?
13. На одном конце платформы длиной 10 м и массой 240 кг стоит человек массой 60 кг. Каково будет перемещение платформы относительно земли, когда человек перейдет к ее противоположному концу? Подсказка.
Примите, что человек идет с постоянной скоростью v относительно платформы; выразите через v скорость платформы относительно земли.
14. В лежащий на длинном столе деревянный брусок массой M попадает летящая горизонтально со скоростью и пуля массой m и застревает в нем. Сколько времени после этого брусок будет скользить по столу, если коэффициент трения между столом и бруском равен μ?
(1 votes, average: 5,00 out of 5)