Условия равновесия тела
1. Первое условие равновесия тела
Выясним, при каких условиях тело, покоящееся относительно некоторой инерциальной системы отсчета, останется в покое.
Если тело покоится, то его ускорение равно нулю. Тогда согласно второму закону Ньютона должна быть равна нулю и равнодействующая приложенных к телу сил. Поэтому первое условие равновесия можно сформулировать так:
Если тело находится в покое, то векторная сумма (равнодействующая) приложенных к нему сил равна нулю: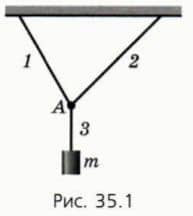 
Заметим, что одного условия
В случаях, когда покоящееся в начальный момент тело может рассматриваться как материальная точка, первого условия равновесия достаточно, чтобы тело осталось в покое. Рассмотрим примеры.
Пусть груз массой m подвешен на трех тросах и покоится (рис. 35.1). Узел А, связывающий тросы, можно считать материальной точкой, которая находится в равновесии.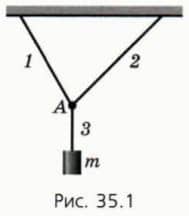 
Следовательно, векторная сумма приложенных к узлу А сил натяжения нитей равна нулю (рис.
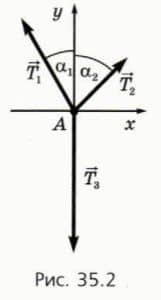
35.2):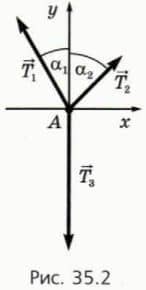 
Покажем два способа применения этого уравнения при решении задач.
Используем проекции векторов. Выберем оси координат и обозначим углы между тросами 1, 2 и вертикалью, как показано на рисунке 35.2.
? 1. Объясните, почему в данном случае справедливы следующие уравнения:
Ox: — T1 sin α1 + T2 sin α2 = 0, Oy: T1 cos α1 + T2 cos α2 — T3 = 0, T3 = mg.
Воспользуйтесь этой системой уравнений при выполнении следующих заданий.
? 2. Чему равна сила натяжения каждого троса, если m = 10 кг, α1 = α2 = 30º?
? 3. Известно, что T1 = 15 Н, α1 = 30º, α2 = 45º. Чему равны: а) сила натяжения второго троса T2? 5) масса груза m?
? 4. Пусть α1 = α2. Чему равны эти углы, если сила натяжения каждого троса: а) равна весу груза? б) в 10 раз больше веса груза?
Итак, силы, действующие на подвесы, могут многократно превышать вес груза!
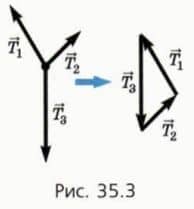
Воспользуемся тем, что три вектора, сумма которых равна нулю, «замыкаются» в треугольник (рис. 35.3). Рассмотрим пример.
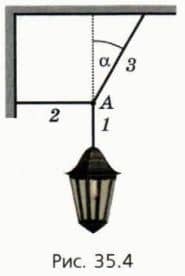
? 5. Фонарь массой m подвешен на трех тросах (рис. 35.4). Обозначим модули сил натяжения тросов T1, T2, T3. Угол α ≠ 0. а) Изобразите силы, действующие на узел A, и объясните, почему T3 > mg и T3 > T2.
б) Выразите T3 через m, g и T2. Подсказка. Векторы сил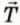 
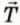1, 2 и 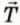3 образуют прямоугольный треугольник.
2. Второе условие равновесия тела (правило моментов)
Убедимся на опыте в том, что одного первого условия равновесия недостаточно для того, чтобы тело оставалось в покое.
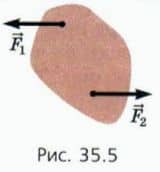
Поставим опыт Прикрепим к куску картона две нити и потянем за них в противоположные стороны с равными по модулю силами (рис. 35.5). Векторная сумма приложенных к картону сил равна нулю, но он не останется в покое, а начнет поворачиваться.
Условие равновесие тела, закрепленного на оси
Второе условие равновесия тела — обобщение условия равновесия тела, закрепленного на оси. Оно знакомо вам из курса физики основной школы. (Это условие является следствием закона сохранения энергии в механике.) Напомним его.
Пусть на тело, закрепленное на оси О, действуют силы 
1 и 2 (рис. 35.6). Тело может находиться в равновесии только при условии, что
F1l1 = F2l2 (2)
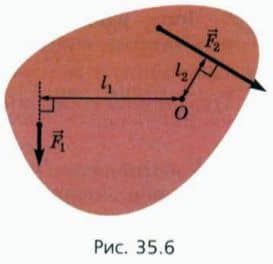Здесь l1 и l2 — плечи сил, то расстояния от оси вращения О до линии действия сил 1 и 2.
Чтобы найти плечо силы, надо линию действия силы и опустить перпендикуляр из оси вращения на эту линию. Его длина и есть плечо силы.
? 6. Перенесите в тетрадь рисунок 35.7. Одной клетке соответствует 1 м. Чему равны плечи сил 1, 2, 3, 4?
Вращающее действие силы характеризуют моментом силы. Модуль момента силы равен произведению модуля силы на ее плечо. Момент силы считают положительным, если сила стремится вращать тело против часовой стрелки, и отрицательным — если по часовой стрелке. (Таким образом, знак момента силы, вращающей тело в какую-то сторону, совпадает со знакомым вам из школьного курса математики знаком угла поворота в ту же сторону на единичной окружности.)
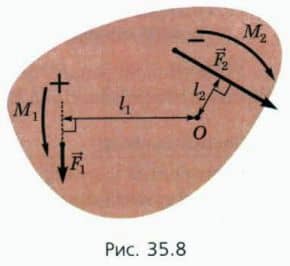
Например, моменты изображенных на рисунке 35.8 сил относительно точки О таковы:
M1 = F1l1; M2 = — F2l2.
Момент силы измеряется в ньютонах * метрах (Н * м).
? 7. Чему равны моменты изображенных на рисунке 35.7 сил относительно точки О? Одной клетке соответствует расстояние 1 м, а также сила 1 Н.
Перепишем соотношение (2), используя моменты сил: M1 + M2 = 0. (3) Это соотношение называют правилом моментов.
Если на покоящееся тело, закрепленное на оси, действуют несколько сил, то оно останется в покое только при условии, что алгебраическая сумма моментов всех этих сил равна нулю:
M1 + M2 + … + Mn = 0.
Заметим, что одного этого условия недостаточно для того, чтобы тело покоилось. Если алгебраическая сумма моментов приложенных к телу сил равна нулю, но в начальный момент тело вращается, то оно будет продолжать вращаться с той же угловой скоростью.
Чтобы убедиться в этом, раскрутите велосипедное колесо приподнятого велосипеда или юлу. После этого они будут вращаться довольно долго: тормозить их будет только небольшая сила трения. Да и наша Земля миллиарды лет вращается вокруг своей оси, хотя вокруг оси никакие силы Землю не вращают!
Условие равновесия тела, не закрепленного на оси
Учтем теперь силу, действующую на закрепленное на оси тело со стороны оси. Так, рассмотренное выше тело (рис. 35.6) на самом деле находится в равновесии под действием трех сил: 1, 2 и 3 (рис.
35.9, а).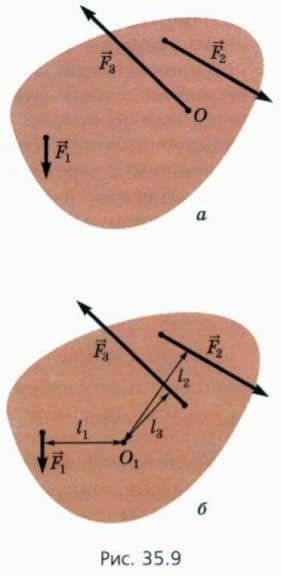 
А теперь заметим, что покоящееся тело не вращается вокруг любой оси.
Поэтому второе условие равновесия для тела, не закрепленного на оси, можно сформулировать так:
Чтобы тело оставалось в покое, необходимо, чтобы алгебраическая сумма моментов всех приложенных к телу сил относительно любой оси была равна нулю:
M1 + M2 + … + Mn = 0. (4)
(Мы считаем, что все приложенные к телу силы лежат в одной плоскости.)
Например, кусок картона, покоящийся под действием сил 1, 2 и 3 (рис. 35.9, б), можно закрепить иглой в произвольной точке О1. Тело «не заметит» новой оси вращения O1: оно как было, так и останется в покое.
При решении задач ось, относительно которой находят моменты сил, часто проводят через точку приложения силы или сил, которые не заданы в условии: тогда их моменты относительно этой оси равны нулю. Например, в следующем задании в качестве такой оси удобно взять нижний конец стержня.
Заметим, что одного второго условия равновесия также недостаточно для того, чтобы тело осталось в покое.
Покоящееся в начальный момент тело останется в покое только в том случае, если равны нулю и равнодействующая приложенных к телу сил, и алгебраическая сумма моментов этих сил относительно любой оси. (Строго говоря, для этого необходимо еще, чтобы равновесие было устойчивым (см. § 36).)
? 8. Верхний конец покоящегося легкого стержня длиной L удерживается горизонтальным тросом (рис. 35.10). Нижний конец стержня закреплен в шарнире (стержень может вращаться вокруг нижнего конца).
Угол между стержнем и вертикалью равен α. К середине стержня подвешен груз массой m. Трением в шарнире можно пренебречь. Изобразите на чертеже вес груза m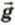
и силу натяжения троса 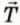, которые действуют на стержень. Чему равны: а) плечо и момент силы тяжести относительно точки O? б) плечо и момент силы 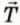относительно точки O? в) модуль силы ?
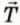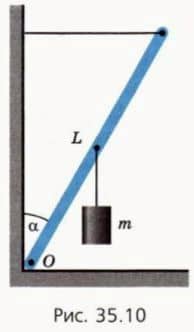
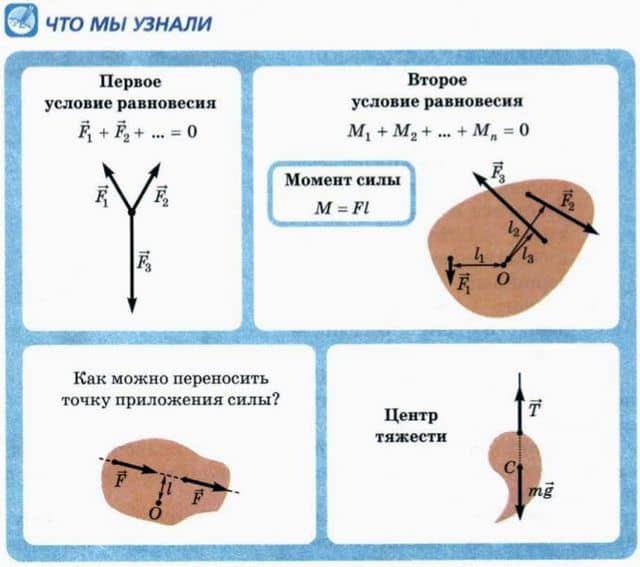
Как можно переносить точку приложения силы?
Перенесем точку приложения сил из A в B вдоль линии действия силы (рис. 35.11).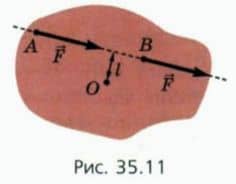 
При этом: — не изменится векторная сумма действующих на тело сил; — не изменится момент этой силы относительно любой оси, потому что не изменилось плечо l этой силы.
Итак, точку приложения силы можно переносить вдоль линии ее действия, не нарушая равновесия тела.
? 9. Объясните, почему тело может находиться в покое под действием трех непараллельных сил только при условии, что линии их действия пересекаются в одной точке (рис. 35.12).
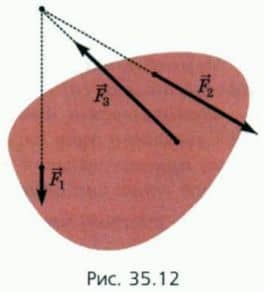Обратите внимание: точка пересечения линий действия этих сил может находиться (и часто находится!) вне тела.
? 10. Вернемся к заданию 8 (рис. 35.10). а) Найдите точку пересечения линий действия веса груза и силы натяжения троса.
б) Найдите графически направление силы, действующей на стержень со стороны шарнира. в) Куда надо перенести точку крепления горизонтально направленного троса, чтобы сила, действующая на стержень со стороны шарнира, была направлена вдоль стержня?
3. Центр тяжести
Центром тяжести называют точку приложения силы тяжести. Будем обозначать центр тяжести буквой С. Центр тяжести однородного тела правильной геометрической формы совпадает с его геометрическим центром.
Например, центр тяжести однородного:
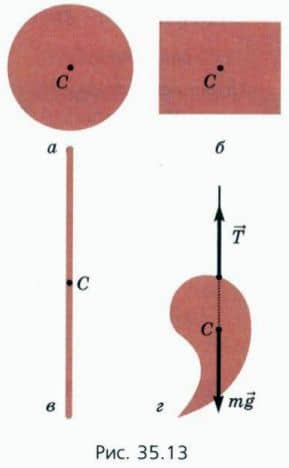
- Диска совпадает с центром диска (рис. 35.13, а); Прямоугольника (в частности, квадрата) совпадает с точкой пересечения диагоналей (рис. 35.13, б); Прямоугольного параллелепипеда (в частности, куба) совпадает с точкой пересечения диагоналей, соединяющих противоположные вершины; Тонкого стержня совпадает с его серединой (рис. 35.13, в).
Для тел произвольной формы положение центра тяжести находят опытным путем:
Если тело, подвешенное в одной точке, находится в равновесии, то его центр тяжести лежит на одной вертикали с точкой подвеса (рис. 35.13, г).
Действительно, если центр тяжести и точка подвеса не будут на одной вертикали, то алгебраическая сумма моментов силы тяжести и силы, действующей со стороны подвеса, не будет равна нулю (например, относительно центра тяжести).
Алгебраическая сумма моментов сил тяжести, действующих на все части тела, относительно центра тяжести тела равна нулю. (Иначе его невозможно было бы подвесить в одной точке.)
Это используют при расчете положения центра тяжести.
? 11. На концах легкого стержня длиной l укреплены шарики массой m1 и m2. На каком расстоянии от первого шарика находится центр тяжести этой системы?
? 12. Горизонтально расположенная однородная балка длиной 1 м и массой 100 кг висит на двух вертикальных тросах. Синий трос укреплен на расстоянии 20 см от левого конца балки, а зеленый — на расстоянии 30 см от ее правого конца.
Изобразите на чертеже действующие на балку силы и их плечи относительно центра тяжести балки. Чему равны: а) плечи сил? б) силы натяжения тросов?
Дополнительные вопросы и задания
13. На одинаковой высоте на расстоянии 1 м друг от друга закреплены концы нерастяжимого троса длиной 2 м. Какой максимальной массы груз можно подвесить к середине троса, чтобы сила натяжения троса не превышала 100 Н?
14. Фонарь подвешен на двух тросах. Силы натяжения тросов равны 10 Н и 20 Н, а угол между тросами равен 120º. Чему равна масса m фонаря? Подсказка.
Если сумма трех векторов равна нулю, то они образуют треугольник.
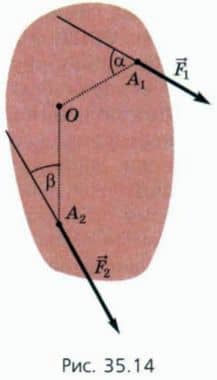
15. К куску картона, закрепленному на оси О, в точках А1 и А2 прикладывают силы 1 и 2 (рис. 35.14). Известно, что ОА1 = 15 см, ОА2 = 20 см, F1 = 20 Н, F2 = 30 Н, α = 60º, β = 30º.
а) Чему равны плечи сил 1 и 2? б) Чему равны моменты этих сил (с учетом знака)? в) Может ли картон остаться в покое?
А если нет, то в какую сторону он начнет вращаться?
16. Два человека несут цилиндрическую трубу массой 30 кг и длиной 4 м. Первый держит трубу на расстоянии 1,2 м от конца. На каком расстоянии от другого конца держит трубу второй чело, век, если нагрузка на его плечо составляет 100 Н?
17. Легкий стержень длиной 1 м закреплен на горизонтальной оси. Если к левому концу стержня подвесить некоторый груз, а к правому — гирю массой 1 кг, то стержень будет находиться в равновесии. А если тот же груз подвесить к правому концу стержня, то стержень будет находиться в равновесии, если к его левому концу подвешена гиря массой 16 кг.
а) Чему равна масса груза? б) На каком расстоянии от центра стержня находится ось?
(1 votes, average: 5,00 out of 5)