План-конспект урока по физике. Тема: Гармонические колебания
Цель урока: сформировать у учащихся представление о гармонических колебаниях, как о гармонических изменениях координаты и других физических величин; ввести понятие амплитуды, периода, частоты, циклической частоты; получить формулу для вычисления периода свободных колебаний.
Ход урока
Проверка домашнего задания методом индивидуального опроса
1. Пояснить, используя чертеж, какие силы заставляют колебаться математический маятник.
2. Получить уравнение движение для пружинного маятника. у доски)
3.
Изучение нового материала
1. Изучив зависимость ускорения от координаты колеблющегося тела, найдем зависимость координаты от времени.
2. Ускорение – вторая производная координаты по времени.
а = — k x/m; x“= — k x/m; где х“- вторая производная координаты по времени.
Если колебания свободные, то координата х со временем изменяется так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.
3. Гармонические колебания
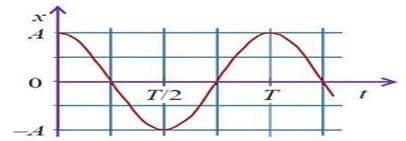
Координата х меняется со временем периодически. Нам известны две периодические функции: синус и косинус
Косинус при возрастании аргумента от нуля меняется медленно, приближаясь к нулю его изменения, происходят все быстрее.
Пружинный маятник, выведенный из положения равновесия, ведет себя точно так же. Синус и косинус обладают свойством, что вторая производная этих функций пропорциональна самим функциям, взятым с противоположным знаком.
На основании этого можно утверждать, что координата тела, совершающего свободные колебания, изменяется со временем по закону косинуса или синуса.
Периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса, называются гармоническими колебаниями.
4. Амплитуда колебаний
Модуль наибольшего смещения тела от положения равновесия называют амплитудой гармонических колебаний.
Амплитуда — характеристика колебательного движения; она показывает как смещено тело от положения равновесия.
5. Решение уравнения движения, описывающего свободные колебания. Запишем решение уравнения; х“= — k x/m; — X= xm QUOTE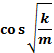 
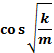·t; Первая производная будет иметь вид: Xʹ= — QUOTE 
xm QUOTE 
·t;
вторая производная будет равна: X“= — QUOTE 
xm QUOTE 
·t = — k x/m; то есть мы, получили первоначальное уравнение. Решением этого уравнения будет также и функция; QUOTE 
·t
Из опытов получили
а= — k x/m a= — g x/L
для пружинного для математического маятника маятника
ОБОЗНАЧИМ
k/m ω02 g/L
Имеем уравнения движения
а= — ω02x Подчиняются одной закономерности a= — ω02x
a ~x x~x“ x “= — ω02x – решением этого дифференциального уравнения
является: x = xm QUOTE 
. График зависимости координаты от времени представляет собой косинусоиду. Гармонические колебания происходят по этому закону.
6. Период и частота гармонических колебаний
Период – время одного колебания. Т=t/n; T= 1/γ; T=2π/ω0 Измеряется в 1с. | Частота – это число колебаний в единицу времени. γ= 1/Т; γ= ω0/2π Измеряется в 1/с; 1Гц | Циклическая (круговая) частота – число колебаний за 2π секунд. ω0 Т= 2π; ω0=2π/Т = 2πγ |
Закрепление изученного материала
Задача. Груз колеблющийся на пружине, за 8 с совершил 32 колебания. Найти частоту и период колебаний.
Решение. Т=t/n; γ = 1/T; T= 8/32 = 0,25 c; γ= 1/0,25 = 4 Гц
Подведем итоги урока
Домашнее задание: § 21, упр. 3, № 1, 2.
(1 votes, average: 5,00 out of 5)