Прямолинейное неравномерное движение. Средняя скорость
Как вы понимаете, в жизни практически невозможно встретить тело, движущееся точно равномерно. Поэтому мы с вами переходим к изучению более сложных видов движения. Рассмотрим простой пример.
Пусть автомобиль, который едет из Москвы в Санкт-Петербург по прямой, за 10 ч проезжает 600 км (рис. 50). Будем считать автомобиль точечным телом, так как его размеры по сравнению с пройденным расстоянием пренебрежимо малы. Понятно, что за время своего движения автомобиль многократно разгонялся и тормозил и даже стоял перед светофорами.
В результате движение

Для таких случаев вводят понятие «средняя путевая скорость». В рассмотренном примере за время t = 10 ч автомобиль проехал путь s = 600 км. Средняя путевая скорость автомобиля при этом равна
Vср. п = s/t = 600 км / 10 ч = 60 км/ч.
Средней путевой скоростью тела называют физическую величину, равную отношению пути, пройденного телом за рассматриваемый промежуток времени, к длительности этого промежутка.
Vср. п = s/t
Обратим внимание на то, что путь s не имеет направления и является скалярной неотрицательной величиной. Поэтому и средняя путевая скорость vср. п всегда является скалярной неотрицательной величиной. Она не имеет направления, а следовательно, не является вектором.
Средняя путевая скорость vср. п — скалярная неотрицательная величина.
Теперь рассмотрим определение еще одной физической величины, которая связана не с путем, пройденным телом, а с его перемещением за рассматриваемый промежуток времени. Введем систему отсчета так, как показано на рис. 50.
В результате мы найдем, что за время t = 10 ч автомобиль совершил перемещение Δx в положительном направлении оси X, модуль которого |Δx| = 600 км.
Средней скоростью тела за промежуток времени t называют физическую величину, равную отношению перемещения Δx, совершенного телом, к длительности этого промежутка времени.
Vср = Δx/t
Поскольку перемещение Δx является вектором, то средняя скорость — тоже вектор. Направление средней скорости vср совпадает с направлением перемещения Δx.
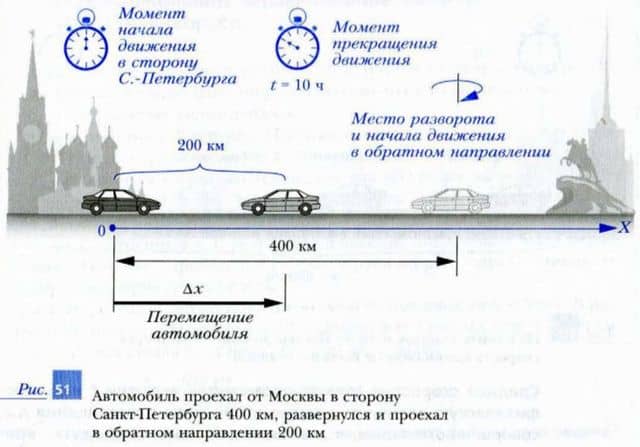
Чтобы лучше понять, чем отличаются друг от друга средняя скорость и средняя путевая скорость, обратимся к рис. 51. Пусть автомобиль, выехавший из Москвы в Санкт-Петербург, находился в пути 10 ч. При этом, проехав 400 км в сторону Санкт-Петербурга, он повернул обратно и проехал 200 км в сторону Москвы. Ясно, что путь, пройденный автомобилем за 10 ч, равен (400 + 200) км = 600 км.
Значение перемещения автомобиля за то же время равно (400 — 200) км = 200 км. Используя данные определения, найдем среднюю путевую скорость и значение средней скорости автомобиля за 10 ч движения:
Vср. п = s/t = 600 км / 10 ч = 60 км/ч; vср = Δx/t = 200 км / 10 ч = 20 км/ч.
Итоги
Средняя путевая скорость — это физическая величина, равная отношению пути, пройденного телом за рассматриваемый промежуток времени, к длительности этого промежутка.
Vср. п = s/t
Средняя путевая скорость — скалярная неотрицательная величина.
Средняя скорость тела за промежуток времени t — это физическая величина, равная отношению перемещения Δx, совершенного телом, к длительности этого промежутка времени.
Vср = Δx/t
Средняя скорость — вектор. Она направлена туда, куда направлено перемещение тела за рассматриваемый промежуток времени.
Если тело все время движется в одном направлении, то модуль средней скорости равен средней путевой скорости. Если же в процессе своего движения тело меняет направление движения, то модуль средней скорости меньше средней путевой скорости.
Вопросы
Дайте определение средней скорости и средней путевой скорости. Какая из этих величин является векторной? Почему средняя путевая скорость не может быть отрицательной? Чему равно значение средней скорости за промежуток времени, в течение которого перемещение тела было равно нулю? Всегда ли будет равна нулю средняя путевая скорость за этот же промежуток времени? Приведите примеры.
Упражнения
1. Пусть автомобиль проехал за первый час 90 км в положительном направлении оси X, а за второй час — 70 км в противоположном направлении. Определите среднюю путевую скорость автомобиля и значение его средней скорости: а) за первый час; б) за второй час; в) за первые два часа движения. Объясните, почему эти скорости отличаются друг от друга.
2.Представьте себе, что вы выехали на автомобиле со стоянки, находящейся рядом с вашим домом, в 8 часов утра. В 17 часов вечера вы вернули автомобиль на прежнее место. За день вы проехали путь s = 380 км, при этом в течение промежутка времени от 10 до 12 часов дня вы ехали по прямолинейной трассе строго на север с постоянной скоростью 60 км/ч. Ответьте на вопросы: а) чему была равна ваша средняя путевая скорость за время с 8 часов утра до 17 часов вечера?
б) какова была ваша средняя скорость за интервалы времени: с 8 до 17 часов; с 10 до 12 часов?
3. Определите значение средней скорости и среднюю путевую скорость за промежуток времени от момента времени t0 = 0 до момента времени t2 = 7 с для тела, график движения которого приведен на рис. 47.
4. А) Измерьте шагами свой путь от дома до школы и время движения. Переведите это расстояние в метры, а время в секунды. Считайте, что длина одного шага приблизительно равна 0,6 м. Вычислите свою среднюю путевую скорость.
Проделайте тот же путь на велосипеде и по результатам измерений найдите среднюю путевую скорость. Б) Используя карту местности, найдите расстояние по прямой от дома до школы, чтобы затем рассчитать среднюю скорость при движении пешком и на велосипеде.
