Home ⇒ 📌Физика ⇒ Сложение скоростей и переход в другую систему отсчета при движении вдоль одной прямой

Сложение скоростей и переход в другую систему отсчета при движении вдоль одной прямой

1. Сложение скоростей

В некоторых задачах рассматривается движение тела относительно другого тела, которое также движется в выбранной системе отсчета. Рассмотрим пример.

По реке плывет плот, а по плоту идет человек в направлении течения реки — в том направлении, куда плывет плот (рис. 3.1, а). Используя установленный на плоту столб, можно отмечать как перемещение плота относительно берега, так и перемещение человека относительно плота.

Обозначим вектор скоростиЧп скорость человека относительно

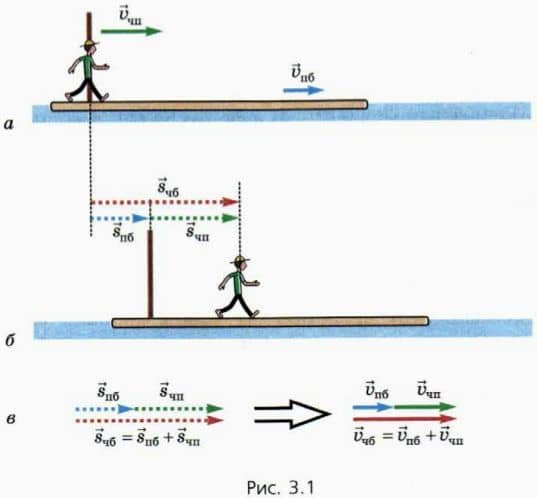
плота, а вектор скоростиПб — скорость плота относительно берега. (Обычно принимают, что скорость плота относительно берега равна скорости течения реки. Скорость и перемещение тела 1 относительно тела 2 мы будем обозначать с помощью двух индексов: первый индекс относится к телу 1, а второй — к телу 2. Например, вектор скорости12 обозначает скорость тела 1 относительно тела 2.) сложение перемещений и скоростей

Рассмотрим перемещения человека и плота за некоторый промежуток времени t.

Обозначим 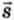вектор перемещенияПб перемещение плота относительно берега, а 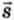вектор перемещенияЧп — перемещение человека относительно плота (рис. 3.1, б).

Векторы перемещений изображены на рисунках пунктирными стрелками, чтобы отличить их от векторов скоростей, изображенных сплошными стрелками.

Перемещение 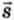вектор перемещенияЧб человека относительно берега равно векторной сумме перемещения человека относительно плота и перемещения плота относительно берега (рис. 3.1, в):

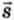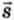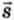вектор перемещенияЧб = вектор перемещенияПб + вектор перемещенияЧп (1)

Свяжем теперь перемещения со скоростями и промежутком времени t. Мы получим:

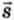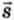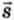вектор перемещенияЧп = вектор скоростиЧпt, (2) вектор перемещенияПб = вектор скоростиПбt, (3) вектор перемещенияЧб = вектор скоростиЧбt, (4)

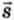Где вектор перемещенияЧб — скорость человека относительно берега. Подставляя формулы (2-4) в формулу (1), получаем:

вектор скоростиЧбt = вектор скоростиПбt + вектор скоростиЧпt.

Сократим обе части этого уравнения на t и получим:

вектор скоростиЧб = вектор скоростиПб + вектор скоростиЧп. (5)

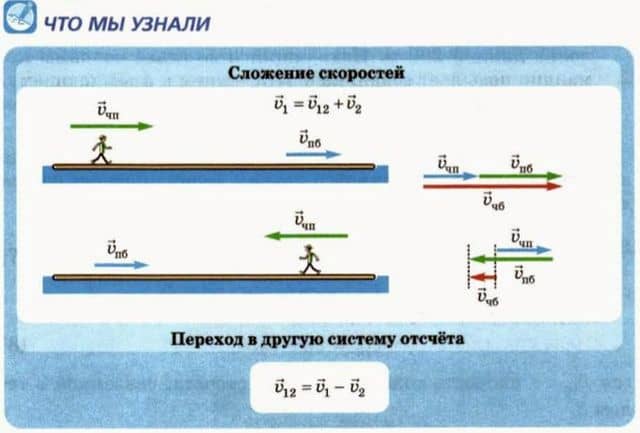
Правило сложение скоростей

Соотношение (5) представляет собой правило сложения скоростей. Оно является следствием сложения перемещений (см. рис. 3.1, в, внизу). В общем виде правило сложения скоростей выглядит так:

вектор скорости1 = вектор скорости12 + вектор скорости2. (6)

Где вектор скорости1 и вектор скорости2 — скорости тел 1 и 2 в одной и той же системе отсчета, а вектор скорости12 — скорость тела 1 относительно тела 2.

Итак, скорость вектор скорости1 тела 1 в данной системе отсчета равна векторной сумме скорости вектор скорости12 тела 1 относительно тела 2 и скорости вектор скорости2 тела 2 в той же системе отсчета.

В рассмотренном выше примере скорость человека относительно плота и скорость плота относительно берега были направлены одинаково. Рассмотрите теперь случай, когда они направлены противоположно, Не забудьте, что скорости надо складывать по правилу сложения векторов!

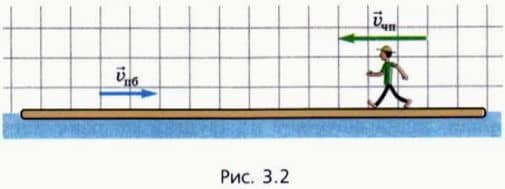
? 1. Человек идет по плоту против течения (рис. 3.2). Сделайте в тетради чертеж, с помощью которого можно найти скорость человека относительно берега.

Масштаб для вектора скорости: две клетки соответствуют 1 м/с.

Уметь складывать скорости необходимо при решении задач, в которых рассматривается движение лодок или судов по реке или полет самолета при наличии ветра. При этом текущую воду или движущийся воздух можно представлять себе как «плот», который движется с постоянной скоростью относительно земли, «неся» на себе суда, самолеты и пр.

Например, скорость плывущей по реке лодки относительно берега равна векторной сумме скорости лодки относительно воды и скорости течения реки.

? 2. Скорость моторной лодки относительно воды равна 8 км/ч, а скорость течения равна 4 км/ч. За сколько времени лодка проплывет от пристани А до пристани Б и обратно, если расстояние между ними 12 км?

? 3. От пристани А одновременно отплыли плот и моторная лодка. За то время, пока лодка доплыла до пристани Б, плот проплыл треть этого расстояния. а) Во сколько раз скорость лодки относительно воды больше скорости течения? б) Во сколько раз время движения лодки из Б в А больше, чем время ее движения из А в Б?

? 4. Самолет пролетел из города М в город Н за 1,5 ч при попутном ветре. Обратный перелет при встречном ветре занял 1 ч 50 мин. Скорость самолета относительно воздуха и скорость ветра оставались постоянными. а) Во сколько раз скорость самолета относительно воздуха больше скорости ветра?

б) Сколько времени занял бы перелет из М в Н в безветренную погоду?

2. Переход в другую систему отсчета

Проследить за движением двух тел намного проще, если перейти в систему отсчета, связанную с одним из этих тел. Тело, с которым связана система отсчета, покоится относительно нее, поэтому следить надо только за другим телом.

Рассмотрим примеры.

Моторная лодка обгоняет плывущий по реке плот. Через час после этого она разворачивается и плывет обратно. Скорость лодки относительно воды 8 км/ч, скорость течения 2 км/ч.

Через какое время после разворота лодка встретит плот?

Если решать эту задачу в системе отсчета, связанной с берегом, то пришлось бы следить за движением двух тел — плота и лодки, да еще учесть при этом, что скорость лодки относительно берега зависит от скорости течения.

Если же перейти в систему отсчета, связанную с плотом, то плот и река «остановятся»: ведь плот движется по реке как раз со скоростью течения. Поэтому в этой системе отсчета все происходит как в озере, где течения нет: лодка плывет от плота и к плоту с одинаковой по модулю скоростью! И раз она удалялась в течение часа, то через час она приплывет обратно.

Как видим, для решения задачи не понадобились ни скорость течения, ни скорость лодки.

? 5. Проезжая под мостом на лодке, человек уронил в воду соломенную шляпу. Через полчаса он обнаружил пропажу, поплыл обратно и нашел плывущую шляпу на расстоянии 1 км от моста. Сначала лодка плыла по течению и ее скорость относительно воды была равна 6 км/ч.

Перейдите в систему отсчета, связанную со шляпой (рис. 3.3), и ответьте на следующие вопросы. а) Сколько времени человек плыл к шляпе?

б) Чему равна скорость течения? в) Какая информация в условии не нужна для ответа на эти вопросы?

3.3

? 6. По прямой дороге со скоростью 1 м/с идет пешая колонна длиной 200 м. Находящийся во главе колонны командир посылает всадника с поручением к замыкающему. Через сколько времени всадник вернется обратно, если он скачет со скоростью 9 м/с?

Выведем общую формулу для нахождения скорости тела в системе отсчета, связанной с другим телом. Воспользуемся для этого правилом сложения скоростей.

Напомним, что оно выражается формулой

вектор скорости1 = вектор скорости2 + вектор скорости12, (7)

Где вектор скорости12 — скорость тела 1 относительно тела 2.

Перепишем формулу (1) в виде

вектор скорости12 = вектор скорости1 — вектор скорости2, (8)

Где вектор скорости12 — скорость тела 1 в системе отсчета, связанной с телом 2.

Эта формула позволяет найти скорость вектор скорости12 тела 1 относительно тела 2, если известны скорость вектор скорости1 тела 1 и скорость вектор скорости2 тела 2.

? 7. На рисунке 3.4 изображены три автомобиля, скорости которых даны в масштабе: двум клеткам соответствует скорость 10 м/с. 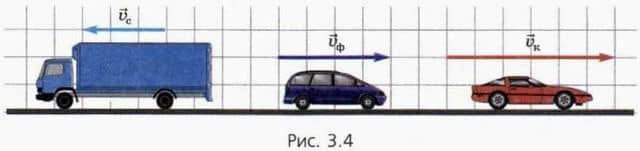Найдите: а) скорость синего и фиолетового автомобилей в системе отсчета, связанной с красным автомобилем; б) скорость синего и красного автомобилей в системе отсчета, связанной с фиолетовым автомобилем; в) скорость красного и фиолетового автомобилей в системе отсчета, связанной с синим автомобилем; г) какая (какие) из найденных скоростей наибольшая по модулю? наименьшая?

Дополнительные вопросы и задания

8. Человек прошел по плоту длиной b и вернулся в начальную точку. Скорость человека относительно плота все время направлена вдоль реки и равна по модулю vч, а скорость течения равна vт. Найдите выражение для пути, пройденного человеком относительно берега, если: а) сначала человек шел по направлению течения; б) сначала человек шел в направлении, противоположном течению (рассмотрите все возможные случаи!).

в) Найдите весь путь, пройденный человеком относительно берега: 1) при b = 30 м, vч = 1,5 м/с, vт = 1 м/с; 2) при b = З0 м, vч = 0,5 м/с, vт = 1 м/с.

9. Пассажир идущего поезда заметил, что мимо его окна промчались две встречные электрички с интервалом 6 мин. С каким интервалом они проехали мимо станции2 Скорость поезда 100 км/ч, скорость электричек 60 км/ч.

10. Два человека одновременно начали спуск на эскалаторе. Первый стоял на одной ступеньке. С какой скоростью шел по эскалатору второй, если он спустился в 3 раза быстрее, чем первый?

Скорость эскалатора 0,5 м/с.

11. На эскалаторе 100 ступеней. Идущий вниз по эскалатору человек насчитал 80 ступеней. Во сколько раз скорость человека больше скорости эскалатора?

12. От пристани А одновременно отправились плот и моторная лодка. Пока плот доплыл до пристани Б, лодка сплавала от А до Б и обратно. Расстояние АБ равно 10 км. а) Во сколько раз скорость лодки относительно воды больше скорости течения?

б) Какое расстояние проплыл плот, когда: 1) лодка доплыла до Б? 2) плот встретил лодку, плывущую обратно?

13. Самый быстрый зверь — гепард (рис. 3.5): он может мчаться со скоростью 30 м/с, но не более одной минуты. Гепард заметил антилопу, находящуюся от него на расстоянии 500 м. С какой скоростью должна бежать антилопа, чтобы спастись?


1 Star2 Stars3 Stars4 Stars5 Stars (1 votes, average: 5,00 out of 5)

Related posts:

  1. Сложение скоростей и переход в другую систему отсчета при движении на плоскости 1. Сложение скоростей Пусть человек идет поперек плота, плывущего по реке. При этом скорость человека относительно плота перпендикулярна скорости течения (рис. 9.1, вид сверху). Из правила сложения скоростей (см. § 3) следует: где Чб — скорость человека относительно берега, Чп — скорость человека относительно плота, Пб — скорость плота относительно берега (скорость течения). На рисунке […]...

  2. Движение тел относительно друг друга В предыдущих параграфах мы с вами на конкретных примерах научились решать некоторые виды задач кинематики. При этом мы в качестве тела отсчета выбирали Землю или неподвижные относительно нее тела. Оказывается, такой выбор тела отсчета не всегда является наиболее удачным. Во многих реальных задачах, которые встретятся вам в будущем, удобнее в качестве тела отсчета выбирать какое-либо […]...

  3. Равномерное движение по окружности 1. Основные характеристики равномерного движения по окружности Движение по окружности часто встречается в природе и технике: по траекториям, близким к окружностям, движутся планеты вокруг Солнца, Луна и искусственные спутники Земли, точки колес и вращающихся деталей механизмов. Мы ограничимся в нашем курсе равномерным движением по окружности. Напомним, что равномерным называют движение, при котором тело за любые […]...

  4. Инерциальные системы отсчета. Первый закон Ньютона Вы наверняка помните, что движение любого тела относительно. То есть нельзя сказать, имеет ли тело ускорение, если не указать, в какой системе отсчета рассматривается его движение. Например, в системе отсчета, связанной с Землей, тележка, изображенная на рис. 65, покоилась до того момента, как мы начали на нее действовать. Следовательно, в отсутствие действия на тележку ее […]...

  5. Второй закон Ньютона Прежде чем сформулировать один из важнейших законов механики, подведем итог приобретенным знаниям. Напомним, что пока мы ведем разговор только о точечных телах. При наблюдении за точечным телом из инерциальной системы отсчета выполняются следующие правила (рис. 85). Если сумма всех сил, действующих на тело, равна нулю, то это тело движется равномерно прямолинейно или покоится. Иначе говоря, […]...

  6. Кинетическая энергия Из первых параграфов этой главы следует, что если суммарная работа сил, действующих на тело, положительна, то скорость тела относительно инерциальной системы отсчета увеличивается. Напротив, если эта работа отрицательна, то скорость тела уменьшается. Таким образом, изменение скорости движения тела и работа, совершенная над этим телом, связаны. Найдем эту связь. Пусть на гладкой горизонтальной плоскости в точке […]...

  7. Кинетическая энергия и механическая работа 1. Кинетическая энергия Пусть на покоящееся вначале тело массой m действуют постоянные силы, равнодействующую которых обозначим (рис. 29.1). Если перемещение тела равно , работа равнодействующей Aрд = Fs. (1) Индекс «рд» подчеркивает, что речь идет о работе равнодействующей всех приложенных к телу сил. Дело в том, что мы будем использовать сейчас второй закон Ньютона, согласно […]...

  8. Скорость прямолинейного равномерного движения Представим себе, что мы имеем дело с равномерно движущимся по прямой велосипедистом, который проезжает за каждую секунду не 5 м (как в предыдущем параграфе), а, например, 10 м. При этом выбрана та же система отсчета. Тогда зависимость координаты фары от времени будет выглядеть несколько иначе, так как в правой части полученного нами выражения на месте […]...

  9. Относительность механического движения Итак, мы научились описывать положение точечного тела относительно тела отсчета с помощь координаты тела. Обратимся еще раз к рис. 4. Ясно, что с течением времени координата клада относительно дуба не изменяется. Значит, его положение относительно выбранного нами тела отсчета остается постоянным. В соответствии с введенным определением механического движения можно сказать, что клад не движется (покоится) […]...

  10. Перемещении при прямолинейном равноускоренном движении 1. Нахождение пути по графику зависимости скорости от времени Покажем, как можно найти пройденный телом путь с помощью графика зависимости скорости от времени. Начнем с самого простого случая — равномерного движения. На рисунке 6.1 изображен график зависимости v(t) — скорости от времени. Он представляет собой отрезок прямой, параллельной осн времени, так как при равномерном движении […]...

  11. Положение тела в пространстве Наверняка каждый из вас неоднократно договаривался с другом, родителями или учителем о встрече. При этом всегда возникал вопрос: где встретиться? Хорошо, если намеченное место встречи было известно, и вы могли его назвать или показать. Но как быть, если вы договариваетесь о месте встречи по телефону или сообщаете о нем в письме? Обратимся за примером к […]...

  12. Три закона Ньютона Раздел механики, в котором изучают, как взаимодействие тел влияет на их движение, называют динамикой. Основные законы динамики открыли итальянский ученый Галилео Галилей и английский ученый Исаак Ньютон. Вы изучали эти законы в курсе физики основной школы. Напомним их. 1. Первый закон ньютона (закон инерции) Повторим один из опытов, которые поставил итальянский ученый Галилео Галилей. Поставим […]...

  13. Прямолинейное равноускоренное движение 1. Определение прямолинейного равноускоренного движения Поставим опыт Изучим, как скатывается шарик с наклонной плоскости. На рисунке 5.1 показаны последовательные положения шарика через равные промежутки времени. Видно, что шарик движется неравномерно: пути, проходимые им за последовательные равные промежутки времени, увеличиваются. Следовательно, скорость шарика увеличивается. Движение шарика, скатывающегося с наклонной плоскости, является примером прямолинейного равноускоренного движения. Такое […]...

  14. Движение тел относительно друг друга. Задача «погоня» Рассмотрим теперь, как будет выглядеть решение задачи «погоня» при использовании системы отсчета, связанной с одним из движущихся тел. Диспетчер, взглянув на монитор, увидел, что за паровозом, движущимся со скоростью |vп| = 60 км/ч, следует электровоз со скоростью |vэ| = 90 км/ч. Через какое время tд электровоз догонит паровоз, если расстояние между ними в начальный момент […]...

  15. Свободное падение и движение тела, брошенного вертикально вверх 1. Свободное падение тела Закономерности падения тел открыл Галилео Галилей. Знаменитый опыт с бросанием шаров с наклонной Пизанской башни (рис. 7.1, а) подтвердил его предположение, что если сопротивлением воздуха можно пренебречь, то все тела падают одинаково. Когда с этой башни бросили одновременно пулю и пушечное ядро, они упали практически одновременно (рис. 7.1, б). Падение тел […]...

  16. «Секреты» прямолинейного равноускоренного движения Продолжим исследование прямолинейного равноускоренного движения, начатое в § 6. 1. Средняя скорость Напомним (см. § 6), что при прямолинейном движении в одном направлении путь l численно равен площади фигуры, заключенной под графиком зависимости v(t). Используя этот факт, докажем, что в этом случае средняя скорость равна среднему арифметическому начальной и конечной скорости: Vср = (v0 + […]...

  17. Мгновенная и средняя скорость 1. Мгновенная скорость В этом параграфе мы будем рассматривать неравномерное движение. Однако при этом нам пригодится то, что мы знаем о прямолинейном равномерном движении. На рисунке 4.1 показаны положения разгоняющегося автомобиля на прямом шоссе с интервалом времени 1 с. Стрелка указывает на зеркальце заднего вида, положение которого мы рассмотрим далее более подробно. Мы видим, что […]...

  18. Механическая энергия системы тел. Закон сохранения механической энергии Мы изучали различные виды энергии, которыми обладают тела или системы тел. При этом было установлено, что кинетическая энергия определяется движением тел и их массой и зависит от механических параметров системы (масс тел и их скоростей). Потенциальная энергия системы тел определяется их взаимодействием и также зависит от механических параметров (взаимного положения, т. е. координат тел системы, […]...

  19. Свободное падение тел Падение тел — один из самых часто наблюдаемых видов движения. Изучать падение тел люди начали очень давно. Роняя на землю различные предметы, они установили, что отпущенные без начальной скорости предметы падают вертикально вниз. (Напомним, что вертикалью называют линию отвеса, неподвижного относительно Земли.) На основании этого был сделан вывод: такое движение является прямолинейным. Сложнее было установить […]...

  20. Движение тела, брошенного горизонтально и под углом к горизонту 1. Движение тела, брошенного горизонтально Если сопротивлением воздуха можно пренебречь, то брошенное как угодно тело движется с ускорением свободного падения . Рассмотрим сначала движение тела, брошенного горизонтально со скоростью v_vec0 с высоты h над поверхностью земли (рис. 11.1). В векторном виде зависимость скорости тела от времени t выражается формулой В проекциях на оси координат: Vx […]...

  21. Условия применения закона сохранения импульса Как мы уже говорили, в точности замкнутых систем тел не существует. Поэтому возникает вопрос: в каких случаях можно применять закон сохранения импульса к незамкнутым системам тел? Рассмотрим эти случаи. 1. Внешние силы уравновешивают друг друга или ими можно пренебречь С этим случаем мы уже познакомились в предыдущем параграфе на примере двух взаимодействующих тележек. В качестве […]...

  22. Движение системы тел 1. Гладкая горка и шайба Горка с одной вершиной Пусть на гладком столе покоится гладкая горка массой M и высотой H (рис. 34.1). На нее налетает со скоростью 0 шайба массой m. Двигаясь по горке, шайба не отрывается от нее. Возможны три варианта развития событий. 1) Шайба не достигнет вершины горки и соскользнет по тому […]...

  23. Система отсчета, траектория, путь и перемещение Механика изучает механическое движение, то есть изменение положения тел друг относительно друга с течением времени. Основная задача механики — определение положения тел в заданный момент времени, если известны положение и скорость тел в начальный момент. Движение тел зависит от взаимодействия между ними. Но для изучения взаимодействий тел нужно овладеть понятиями, с помощью которых описывают движение […]...

  24. Относительное движение брошенных тел. Отскок от наклонной плоскости 1. Относительное движение брошенных тел Пусть в некоторый момент (t = 0) из точки A на высоте h начинает падать яблоко (рис. 12.1). Лежащий на траве юный стрелок в тот же момент стреляет из пружинного пистолета, намереваясь попасть «в яблочко». Пистолет находится в точке B на расстоянии d от вертикали, вдоль которой падает яблоко, а […]...

  25. Действие одного тела на другое. Закон инерции Представим себе, что на горизонтальной дороге стоит тележка с песком (рис. 65, а). Если мы начнем ее толкать, то тележка начнет двигаться относительно Земли (рис. 65, б). Ее скорость будет изменяться — у тележки появится ускорение в системе отсчета, связанной с Землей. В этом случае принято говорить, что на тележку подействовали, т. е. тележка испытала […]...

  26. Разрывы и столкновения 1. Разрыв летящего снаряда В этом параграфе мы будем предполагать, что сопротивлением воздуха можно пренебречь. ? 1. Выпущенный вертикально вверх снаряд разорвался в верхней точке траектории на два осколка массой m1 и m2 (рис. 32.1). Чему равно отношение скоростей осколков после разрыва? (Под скоростями до и после разрыва или столкновения здесь и далее мы понимаем […]...

  27. Средняя и мгновенная скорости Сквозь смежную метель мчится, сверкая огнями, экспресс. Вдруг поезд резко затормозил и остановился перед красным сигналом светофора. Никто из пассажиров, вероятно, и не подумал, что именно этот сигнал предупредил катастрофу: без него экспресс на полном ходу врезался бы в товарный поезд, оказавшийся на пути движения экспресса. Прислушаемся к разговору, который происходит в одном из купе […]...

  28. Скорость при равноускоренном движении Теория равноускоренного движения была разработана знаменитым итальянским ученым Галилео Галилеем. В своей книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к Механике и Местному движению», вышедшей в 1638 г., Галилей впервые дал определение равноускоренного движения и доказал ряд теорем, в которых описывались его закономерности. Приступая к изучению равноускоренного прямолинейного движения, выясним сначала, […]...

  29. Скорость Проделаем опыт. Установим на тележку капельницу (рис. 11). Из капельницы через одинаковые промежутки времени падают капли окрашенной жидкости. Если присоединить к тележке груз (как это показано на рисунке 11), то при определенной его величине расстояния между следами, оставленными каплями на бумаге (при движении тележки), могут оказаться равными. Это означает, что тележка за одинаковые промежутки времени […]...

  30. Наука о движении тел Раздел физики, который вы начинаете изучать, называется механикой. Механика — это наука о движении тел. По характеру решаемых задач механику делят на две основные части: кинематику и динамику. В Кинематике (от греческого слова «кинема» — движение) дается описание того, как движутся тела, без выяснения причин, почему они так движутся. Причины, которыми обусловлено то или иное […]...

  31. Ускорение Мы выяснили, что движущийся по дороге автомобиль практически все время изменяет свою скорость. Так, если во время движения водитель нажимает на педаль тормоза, скорость автомобиля уменьшается. Если водитель нажимает на педаль газа, скорость автомобиля, наоборот, возрастает. При этом под словом «скорость» мы подразумеваем, как это было отмечено в предыдущем параграфе, мгновенную скорость. Таким образом, если […]...

  32. Механическое движение Одним из самых простых физических явлений является механическое движение тел. Кто из вас не наблюдал, как движется автомобиль, летит самолет, идут люди и т. д.! Если, однако, спросить, движется ли сейчас здание, в котором вы находитесь, вы, наверное, ответите, что нет. И будете не правы! А движется ли сейчас самолет, который вы видите в небе? […]...

  33. Прямолинейное неравномерное движение. Средняя скорость Как вы понимаете, в жизни практически невозможно встретить тело, движущееся точно равномерно. Поэтому мы с вами переходим к изучению более сложных видов движения. Рассмотрим простой пример. Пусть автомобиль, который едет из Москвы в Санкт-Петербург по прямой, за 10 ч проезжает 600 км (рис. 50). Будем считать автомобиль точечным телом, так как его размеры по сравнению […]...

  34. Абсолютная температура и средняя кинетическая энергия молекул 1. Основное уравнение молекулярно-кинетической теории Идеальный газ. Если потенциальной энергией взаимодействия молекул в газе можно пренебречь по сравнению с кинетической энергией их хаотического движения, то можно считать, что вся внутренняя энергия газа — это сумма кинетических энергий его молекул. Такую упрощенную модель реального газа называют идеальным газом. Молекулярно-кинетическая теория идеального газа объясняет свойства газов, рассмотренные […]...

  35. Закон сохранения энергии в механике 1. Когда механическая энергия сохраняется? Из курса физики основной школы вы уже знаете, что Сумму кинетической и потенциальной энергий называют полной механической энергией. Докажем, что Полная механическая энергия замкнутой системы тел, взаимодействующих посредством сил упругости и тяготения, сохраняется, то есть ее изменение равно нулю: ∆(Ek + Ep) = 0. (1) Это утверждение называют законом сохранения […]...

  36. Импульс — значит толчок Загляните в словарь иностранных слов: «импульс» — от лат. impulsus — толчок, удар, побуждение». Эффект, производимый ударом, всегда вызывал удивление у человека. Почему тяжелый молот, положенный на кусок металла на наковальне, только прижимает его к опоре, а тот же молот ударом молотобойца плющит металл? А в чем секрет старого циркового трюка, когда сокрушительный удар молота […]...

  37. Основные следствия, вытекающие из постулатов теории относительности Цель урока: формировать у учащихся новые представления о пространстве и времени, в соответствии с этим, с новой точки зрения рассмотреть закон сложения скоростей. Ход урока 1. Проверка домашнего задания методом фронтального опроса А) Почему оказалось несостоятельным предположение о возможности мгновенной передачи сигнала из одной точки в другую? Б) Какие привычные представления пришлось пересмотреть из – […]...

  38. Реактивное движение. Освоение космоса 1. Реактивное движение Из закона сохранения импульса следует: чтобы разогнаться, надо что-то оттолкнуть назад. Например, когда человек разбегается, он ногами толкает назад дорогу; автомобиль толкает назад дорогу вращающимися ведущими колесами; гребец веслом толкает назад воду. А что можно оттолкнуть назад, когда вокруг ничего нет — как у ракеты в открытом космосе? В таком случае надо […]...

  39. План-конспект урока по физике по теме: Принцип относительности Галилея Цель урока: сформулировать принцип относительности Галилея; показать на примере, что Земля не является строго инерциальной системой отсчета; продолжить формирование умений решать вычислительные и качественные задачи на применение основных законов механики. Ход урока Проверка домашнего задания методом проведения самостоятельной работы. ВАРИАНТ – 1 На движущийся предмет действует несколько сил, результирующая, которых равна нулю. Какой из представленных […]...

  40. Движение Равномерное движение Величина скорости показывает, какое расстояние s может преодолеть тело за определенное время t. Если машина ехала со скоростью 100 километров в час, это значит, что расстояние в 100 километров машина проехала за один час. Если эта скорость является постоянной, то мы имеем дело с равномерным движением тела. Таким образом, скорость тела определяет отношение […]...

Сложение скоростей и переход в другую систему отсчета при движении вдоль одной прямой
«
»