Второй закон Ньютона
Прежде чем сформулировать один из важнейших законов механики, подведем итог приобретенным знаниям.
Напомним, что пока мы ведем разговор только о точечных телах. При наблюдении за точечным телом из инерциальной системы отсчета выполняются следующие правила (рис. 85).
Если сумма всех сил, действующих на тело, равна нулю, то это тело движется равномерно прямолинейно или покоится. Иначе говоря, его ускорение равно нулю (см. рис. 85, а). Эксперименты показывают, что ускорение a тела увеличивается при увеличении суммы F всех сил, действующих на

Если же при действии равными силами на два покоившихся тела модуль |a1| ускорения первого из них меньше модуля |a2| ускорения второго тела, то масса m1 первого тела больше массы m2 второго (см. рис. 85, г). То есть если |a1| 2|, то m1 > m2.
Таким образом, сумма всех сил, действующих на первоначально покоившееся тело, масса этого тела и его ускорение в ИСО связаны между собой. Ньютон, обобщив все известные ему экспериментальные данные, высказал предположение, что эта связь сохраняется и для движущегося в ИСО тела. При атом выполняются следующие положения.
Ускорение a точечного тела в инерциальной системе отсчета: 1) пропорционально сумме F всех сил, действующих на это тело; 2) обратно пропорционально массе этого тела.
В настоящее время эти положения объединены в утверждение, которое принято называть вторым законом Ньютона.
В инерциальной системе отсчета ускорение a точечного тела равно отношению суммы F всех действующих на него сил к его массе m.
A = F/m.
Обратим внимание на то, что входящая в это выражение F — сумма всех действующих на тело сил. Если мы подставим на место F сумму только части сил, забыв о действии других сил, то это выражение не будет верным (не обратится в тождество).
Второй закон Ньютона является одним из важнейших законов природы. Мы будем использовать этот закон при выводе многих других законов и при решении большого числа задач. Поэтому необходимо подробно разобраться, что утверждает второй закон Ньютона и какие выводы можно сделать о причинах движения тела на основании этого закона.
Для этого проведем его анализ.
I. Представим себе, что на какое-то тело не действуют другие тела или сумма всех действующих на него сил равна нулю. Тогда числитель дроби равен нулю. Следовательно,
A = F/ m = 0/m = 0.
В этом случае ускорение такого тела равно нулю. Иначе говоря, скорость тела не изменяется со временем, а значит, это тело движется равномерно прямолинейно (или покоится) в ИСО.
Заметим, что если ускорение тела в ИСО равно нулю, то сумма всех действующих на него сил также равна нулю. То есть если в выражение m — a = F подставить a = 0, то мы получим F = 0.
II. Теперь отметим, что направление суммы F всех действующих на тело сил совпадает с направлением его ускорения a в ИСО. Поэтому в выбранной системе отсчета значение F суммы всех действующих на тело сил и значение его ускорения а в выбранной системе отсчета всегда имеют одинаковые знаки: если F > 0, то и a > 0, и наоборот, при F
Поэтому второй закон Ньютона можно записать в виде соотношения между значениями суммы всех сил, действующих на тело и его ускорения:
A = F/m.
III. Исследуем теперь, как будет изменяться значение ускорения a тела при изменении значения F суммы всех действующих на него сил.
Если увеличить значение F, например, в два раза, то в два раза увеличится числитель дроби, стоящей в правой части. Так как знаменатель дроби m при этом не изменяется, то в два раза увеличится значение ускорения a тела.
Понятно, что если F уменьшить, например, в 10 раз, то при неизменной массе m уменьшится в 10 раз и значение a. Одним словом, во сколько раз увеличивается (уменьшается) значение суммы всех действующих на тело сил, во столько же раз увеличивается (уменьшается) значение его ускорения a. В этом случае говорят, что значение ускорения тела пропорционально значению суммы всех действующих на тело сил: a ~ F.
IV. Теперь посмотрим, что будет происходить со значением ускорения тела, если изменять его массу, оставляя значение суммы всех действующих на него сил неизменным.
Пусть массу тела увеличили, например, в 10 раз. Тогда знаменатель m дроби в правой части увеличится в 10 раз. Так как числитель дроби остается неизменным, то в 10 раз уменьшится значение ускорения a тела.
Наоборот, если при неизменной сумме сил уменьшить массу тела, например, в два раза, то значение ускорения этого тела увеличится в два раза. Таким образом, во сколько раз увеличивается (уменьшается) масса тела m при неизменной сумме действующих на него сил, во столько раз уменьшается (увеличивается) значение ускорения тела. В этом случае говорят, что значение ускорения тела обратно пропорционально массе m этого тела:
A ~ 1/m.
Выражение m — a = F верно только в инерциальных системах отсчета.
Поясним это на двух примерах.
Пример 1. Имеется кирпич, который лежит на поверхности Земли, как показано на рис. 86. В системе отсчета, связанной с Землей, он покоится.
Так как система отсчета, связанная с Землей, является инерциальной и кирпич в этой системе отсчета имеет нулевое ускорение, мы можем сделать следующий вывод: сумма всех сил, действующих на кирпич, равна нулю.
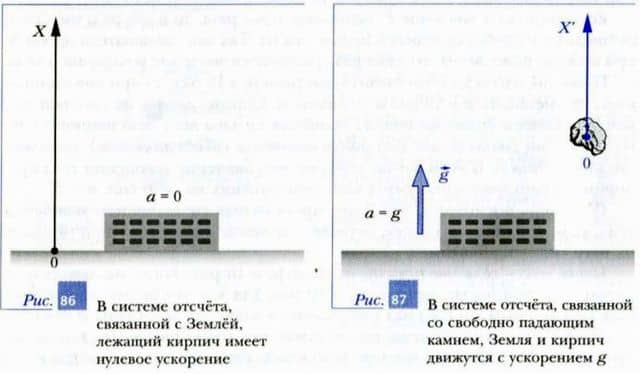
Теперь посмотрим на этот кирпич из системы отсчета, связанной со свободно падающим камнем (рис. 87). В этой системе отсчета падающий камень покоится, а Земля движется с ускорением g в положительном направлении оси X’ (вверх).
Вместе с Землей с ускорением g в том же направлении движется лежащий кирпич. Вместе с тем мы уже знаем, что сумма всех сил, действующих на этот кирпич, равна нулю. Получается, что в системе отсчета X’ лежащий на земле кирпич движется с ускорением a = g, несмотря на то, что сумма всех действующих на него сил равна нулю.
Следовательно, в этой системе отсчета m — a ≠ F. Значит, система отсчета, связанная со свободно падающим камнем, является неинерциальной.
Пример 2. На рис. 88 изображен автобус, резко затормозивший перед сидящим на дороге котом. В результате резкого торможения пассажиры автобуса, которые не держались за поручни, попадали вперед (относительно автобуса). Рассмотрим ситуацию вначале с точки зрения человека, стоящего у обочины дороги (в инерциальной системе отсчета).
На автобус действовала тормозящая сила со стороны дороги, направленная горизонтально в отрицательном направлении оси X. Поэтому скорость автобуса стала уменьшаться. На пассажиров, которые при движении ни за что не держались, в горизонтальном направлении (вдоль оси X) не действовали никакие силы. Поэтому они продолжили движение вперед с постоянной скоростью в инерциальной системе отсчета.
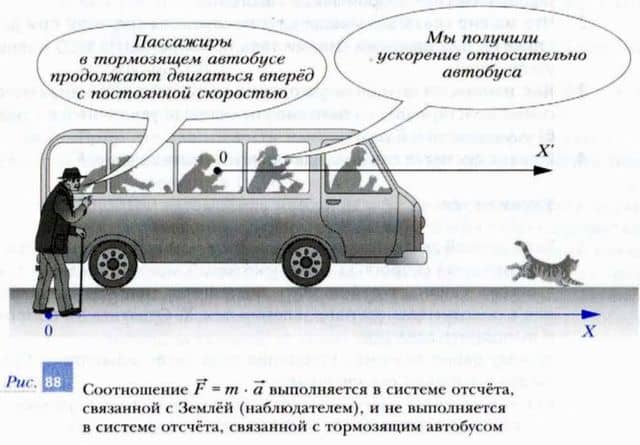
Рассмотрим движение пассажиров в системе отсчета, неподвижной относительно автобуса. Как уже отмечалось, в горизонтальном направлении на пассажиров не действуют никакие силы. Однако в какой-то момент времени их «бросило» вперед. Иначе говоря, в этой системе отсчета (относительно автобуса) их ускорение стало отлично от нуля. Соотношение a = F/m в этом случае не выполняется.
Следовательно, система отсчета, связанная с тормозящим автобусом, не является инерциальной.
Таким образом, мы еще раз убедились, что системы отсчета, связанные с телами, которые движутся относительно Земли (т. е. относительно инерциальной системы отсчета) с ускорением, не являются инерциальными.
Итоги
Второй закон Ньютона. В инерциальной системе отсчета ускорение а точечного тела равно отношению суммы F всех действующих на это тело сил к его массе m.
A = F/m
Зная ускорение a тела массой m в инерциальной системе отсчета, сумму всех сил F, действующих на это тело, можно найти по формуле: F = m — a.
Вопросы
Сформулируйте второй закон Ньютона. Что можно сказать о массах двух покоящихся тел, если при действии на них равными силами тела приобретают в ИСО равные ускорения? Как изменится значение ускорения тела, если при неизменной сумме действующих на тело сил его масса: а) увеличится в 2 раза; б) уменьшится в 5 раз? В каких системах отсчета выполняется соотношение F = m — a?
Упражнения
Тело массой m движется в положительном направлении оси X с постоянной скоростью v0. В некоторый момент времени t0 на это тело начинает действовать постоянная сила F, направленная в положительном направлении оси X. Ответьте на вопросы и выполните задания: а) чему равно значение ускорения тела после момента t0, будет ли это ускорение постоянным; б) как изменится значение скорости тела (увеличится, уменьшится), как будет двигаться тело (разгоняться, тормозиться); в) напишите закон изменения значения скорости тела от времени. Ответьте на вопросы и выполните задания упражнения 1 при условии, что на то же тело в момент времени t0 начинает действовать сила F, направленная в отрицательном направлении оси X. Чему равно значение силы, разгоняющей автомобиль массой m = 1 т = 1000 кг, если значение его ускорения относительно дороги a = 4 м/с2? Определите значение постоянной силы торможения, необходимой для остановки за время t = 4 с автомобиля, который двигался относительно дороги со скоростью v0 = 72 км/ч. Масса автомобиля M = 2 т. Сформулируйте гипотезу о зависимости времени торможения от модуля постоянной тормозящей силы. Обоснуйте ее, используя второй закон Ньютона. На первоначально покоившееся в ИСО тело массой m = 10 кг начинает действовать постоянная сила, значение которой равно: а) F = 100 Н; б) F = 200 Н; в) F = 1000 Н. Определите значения ускорения тела и его скорости через t = 1 с и через t = 2 с после начала движения. Определите значения ускорений в ИСО тела массой m = 2 кг, если на него действуют силы: а) |F1| = 20 Н в положительном направлении оси X и |F2| = 10 Н в отрицательном направлении оси X; б) |F1| = 30 Н и |F2| = 10 Н, направленные в положительном направлении оси X; в) |F1| = 20 Н в положительном направлении оси X и |F2| = 40 Н в отрицательном направлении оси X. Получите зависимость изменения значения скорости v(t) и закон движения x тела из упражнения 6. До начала действия силы тело покоилось в ИСО, x0 = 0. Грузовой автомобиль массой M = 5 т движется по дороге со скоростью, значение которой v0 = 54 км/ч. В некоторый момент водитель нажимает на педаль тормоза, и на автомобиль со стороны дороги начинает действовать постоянная тормозящая сила, модуль которой равен 25 кН. Определите: а) ускорение автомобиля (модуль и направление); б) время торможения автомобиля до полной остановки; в) длину тормозного пути.
