Движение тел относительно друг друга
В предыдущих параграфах мы с вами на конкретных примерах научились решать некоторые виды задач кинематики. При этом мы в качестве тела отсчета выбирали Землю или неподвижные относительно нее тела. Оказывается, такой выбор тела отсчета не всегда является наиболее удачным.
Во многих реальных задачах, которые встретятся вам в будущем, удобнее в качестве тела отсчета выбирать какое-либо тело, движущееся относительно Земли. Понятно, что в такой системе отсчета Земля уже не будет неподвижной. Вместе с Землей в такой системе отсчета будут двигаться
Мы уже сталкивались с таким выбором, когда связывали систему отсчета с идущим по земле человеком. При этом растущий на земле дуб и клад, зарытый в землю, изменяли свои координаты с течением времени. Значит, в системе отсчета, связанной с идущим человеком, они двигались.
Мы говорили тогда, что движение тела зависит от того, в какой системе отсчета оно рассматривается. Изучим теперь этот вопрос подробнее. Для этого рассмотрим одну простую задачу.
Пусть два поезда движутся по параллельным путям навстречу друг другу, как показано на рис. 35. При этом модуль скорости первого поезда |v1| = 10 м/с, а второго — |v2| = 15 м/с.
В первом поезде сидит пассажир, которого мы будем называть наблюдателем.
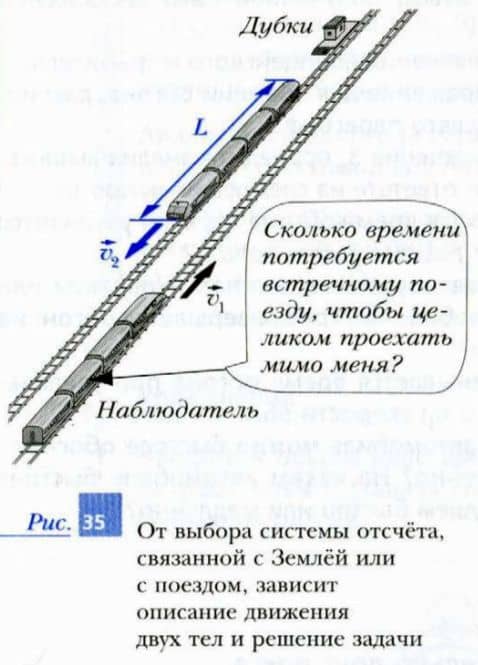
Ответим на вопрос: в течение какого времени второй поезд целиком (от «носа» до «хвоста») проедет мимо наблюдателя, если длина второго поезда L = 175 м?
Понятно, что можно решить эту задачу в системе отсчета, связанной, например, со станцией, пс подвижной относительно Земли. Если вы попробуете сделать это, то убедитесь, что такое решение окажется достаточно сложным. Однако можно существенно упростить решение задачи, если связать систему отсчета непосредственно с наблюдателем.
Сделаем это, используя уже хорошо известный нам алгоритм решения задач кинематики.
Шаг 1. В качестве тела отсчета выберем вагон, в котором находится наблюдатель. Пусть начало отсчета совпадает с наблюдателем. Координатную ось X направим от начала отсчета в сторону движения первого поезда (к станции Дубки). Часы (секундомер) включим в тот момент, когда «нос» второго поезда поравняется с наблюдателем (с началом отсчета).
Этот момент изображен на рис. 36. Можно сказать, что в этот момент второй поезд начал проезжать мимо наблюдателя.
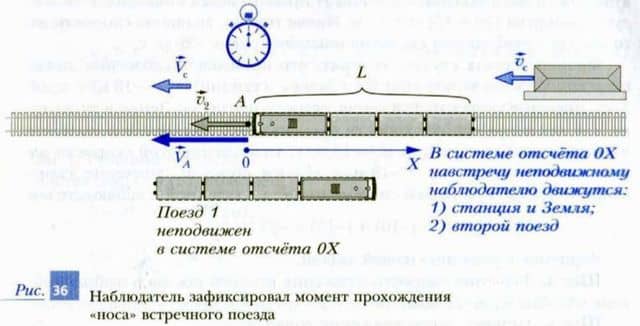
Необходимо отметить, что в данной задаче второй поезд имеет определенные размеры. Поэтому мы не можем считать сто точечным телом. А поскольку мы пока умеем описывать движение только точечных тел, в качестве точки, характеризующей положение второго поезда, выберем точку A — его «нос».
Шаг 2. Определим начальную координату точки A. Из рис. 36 видно, что в выбранной системе отсчета начальная координата точки A равна xA0 = 0.
Теперь начинается самое интересное. Прежде чем продолжить решение, выясним, с какой скоростью движется точка A («нос» второго поезда) в выбранной системе отсчета. Для этого вначале определим, как движутся в этой системе отсчета первый поезд, станции и Земля. Ясно, что относительно наблюдателя первый поезд неподвижен, так как наблюдатель сидит в этом поезде. Напротив, станция в системе отсчета, связанной с наблюдателем, приближается к нему.
Как вы помните, в этом случае вектор скорости станции направлен в отрицательном направлении оси X. Следовательно, значение скорости станции отрицательно. Так как по условию задачи первый поезд движется относительно Земли со скоростью, модуль которой |v1| = 10 м/с, наблюдатель в поезде приближается за каждую секунду к станции на 10 метров. Значит, в системе отсчета, связанной с наблюдателем, станция приближается к нему за каждую секунду на 10 метров.
Следовательно, ее координата уменьшается на 10 метров за каждую секунду. В соответствии с определением значения скорости мы можем сказать, что в выбранной системе отсчета станция движется со скоростью, имеющей значение Vс = -10 м/с. В этой системе отсчета движутся с такой же скоростью и железнодорожное полотно, и деревья, и дома, и вся Земля.
Значения скоростей в нашей системе отсчета мы будем обозначать большими буквами — V, чтобы отличить их от значений скоростей v, которые имели тела в системе отсчета, связанной с Землей. Поэтому значение скорости станции мы обозначили Vс.
Итак, мы выяснили, что в выбранной системе отсчета вся Земля вместе со станцией и железнодорожным полотном движутся в отрицательном направлении оси X со скоростью, имеющей значение Vс = -10 м/с.
По условию задачи по железнодорожному полотну в направлении от станции к первому поезду относительно Земли движется точка A («нос» второго поезда) со скоростью, модуль которой |v2| = 15 м/с. Следовательно, за каждую секунду точка A удаляется от станции в сторону наблюдателя на 15 метров. Сама станция при этом приближается к наблюдателю за одну секунду на 10 метров.
Поэтому точка A приближается к наблюдателю за каждую секунду на (10 + 15) м = 25 м. Иначе говоря, значение скорости второго поезда в выбранной системе отсчета равно -25 м/с.
Физики в таких случаях говорят, что произошло сложение значений скоростей: к значению скорости Земли (станции) Vс = -10 м/с прибавилось значение скорости движения второго поезда по Земле в ту же сторону. Так как направление скорости v2 совпадало с отрицательным направлением оси X, а ее модуль |v2| = 15 м/с, то значение этой скорости отрицательно и равно v2 = -15 м/с. Таким образом, значение скорости второго поезда VA в нашей системе отсчета, связанной с наблюдателем:
VА = Vс + v2 = (-10) + (-15) = -25 (м/с).
Вернемся к решению нашей задачи.
Шаг 3. Значение скорости движения второго поезда в выбранной системе отсчета VА = -25 м/с.
Шаг 4. Запишем закон движения точки A:
XA = xA0 + VA — t = 0 — 25 — t.
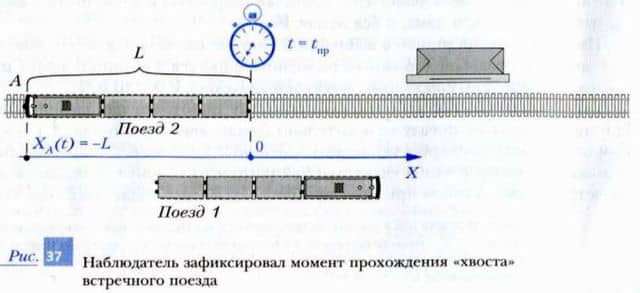
Шаг 5. Запишем в виде уравнения условие задачи. По условию задачи второй поезд должен к искомому моменту времени полностью проехать мимо наблюдателя. Значит, нас интересует тот момент, когда «хвост» второго поезда поравняется с наблюдателем. Этот момент изображен на рис.
37. Легко увидеть, что в этот момент расстояние от точки A до наблюдателя в точности равно длине второго поезда L. Кроме того, значение координаты точки A отрицательно. Следовательно, в этот момент времени
XA = — L = -175 м.
Шаг 6. Объединим составленные уравнения, присвоив каждому номер и название:
XA = xA0 + VA — t = 0 — 25 — t, (1) (закон движения точки A) xA = — L = -175 м. (2) (условие окончания проезда второго поезда мимо наблюдателя)
Шаг 7. Решение уравнений. Подставляя (1) в (2), получаем:
0 — 25 — t = -175 (м), t = -175 м / -25 м/с = 7 с.
Таким образом, второй поезд проедет мимо наблюдателя за t = 7 с.
Итоги Решение задачи, в которой задано движение двух тел относительно третьего (например, Земли), может быть сведено к задаче о движении одного тела, если систему отсчета связать с одним из движущихся тел. При этом решение задач получается более простым.
Вопросы
Как надо выбрать систему отсчета, чтобы одно из движущихся относительно Земли тел в задаче «встреча» стало неподвижным в выбранной системе отсчета? За счет чего произошло сложение значений скоростей в рассмотренной задаче? В какой системе отсчета оно произошло? Увеличилось или уменьшилось значение скорости второго поезда (точки A) в результате сложения скоростей?
Упражнения
Два поезда движутся по параллельным путям навстречу друг другу. Модуль скорости первого поезда |v1| = 5 м/с, а второго — |v2| = 10 м/с. В течение какого времени второй поезд целиком проедет мимо наблюдателя, сидящего в первом поезде? Длина второго поезда L = 150 м. За какое время катер пройдет мимо идущего навстречу ему теплохода? Модуль скорости катера |vк| = 7 м/с, а теплохода — |vт| = 3 м/с. Длина теплохода L = 60 м. Катер считайте точечным телом. Решите задачу из упражнения 1 графическим способом в системе отсчета, связанной с наблюдателем. Решите задачу из упражнения 1 в системе отсчета, связанной с наблюдателем, в общем виде. Проведите анализ полученного решения.
