Движение заряженного тела в электрическом поле
1. Движение вдоль линий напряженности
Рассмотрим сначала случай, когда действующей на тело силой тяжести можно пренебречь по сравнению с силой, которая действует на тело со стороны электрического поля. Это всегда имеет место, когда речь идет о движении заряженных микрочастиц, например электронов. Напомним, кстати, что электрон имеет отрицательный заряд, а протон — положительный.
? 1. Объясните, почему при рассмотрении движения частицы в электрическом поле нельзя пренебрегать массой частицы даже в том случае, когда сила тяжести пренебрежимо
? 2. Заряженная частица движется в однородном электрическом поле. Что можно сказать о начальной скорости этой частицы, если траектория ее движения — прямолинейная?
Рассмотрим, как при таком движении изменяется кинетическая и потенциальная энергия частицы.
? 3. Электрон движется прямолинейно в однородном электрическом поле из точки с потенциалом 700 В в точку с потенциалом 200 В. а) Совпадает ли направление начальной скорости электрона с направлением линий напряженности поля или эти направления противоположны? б) Как изменилась полная энергия электрона? в) Чему равно изменение потенциальной энергии электрона?
г) Чему равно изменение кинетической энергии электрона? д) Какова минимальная начальная скорость электрона?
При движении в электрическом поле заряженная частица может изменить направление движения на противоположное.
? 4. Электрон влетает в однородное электрическое поле с начальной скоростью 8 * 106 м/с. Потенциал поля в точке, в которую влетает электрон, равен 500 В. Направление начальной скорости электрона совпадает с направлением линий напряженности поля. а) До точки с каким минимальным значением потенциала поля долетит электрон?
б) С какой по модулю скоростью электрон вернется в начальную точку? в) Чему равна напряженность поля, если электрон вернулся в начальную точку через 9,1 * 10-9 с? г) Чему равен путь, пройденный электроном до его возвращения в начальную точку?
Сравним движение в одном и том же поле двух частиц с одинаковыми по модулю зарядами, но с различными массами.
? 5. Электрон и протон находятся на одной линии напряженности однородного электрического поля на расстоянии 1 см друг от друга. Они начинают двигаться из состояния покоя в противоположные стороны.
а) Чему равна напряженность поля, если через 10-8 с расстояние между частицами стало равным 9,8 см? б) На какое расстояние от своей начальной точки удалился к этому моменту протон? в) Чему равны в этот момент скорости электрона и протона?
2. Движение заряженной частицы в конденсаторе
Если силой тяжести можно пренебречь по сравнению с силой, действующей на заряженную частицу со стороны электрического поля, то ее движение в поле конденсатора будет аналогично движению тела, брошенного горизонтально или под углом к горизонту, только роль силы тяжести будет играть сила, действующая на заряженную частицу со стороны электрического поля.
? 6. По какой траектории будет двигаться заряженная частица в однородном электрическом поле, если ее начальная скорость направлена под углом к линиям напряженности поля?
При рассмотрении тела, брошенного горизонтально или под углом к горизонту, мы использовали горизонтально направленную ось координат x и вертикально направленную ось y. В данном случае также удобно ввести оси координат x и y, как показано на рисунке 56.1.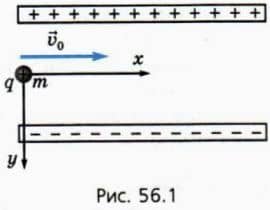 
Если начальная скорость частицы направлена горизонтально, направление оси y удобно выбрать так, чтобы проекция силы, действующей на эту частицу со стороны электрического поля конденсатора, была положительной.
Начало координат совместим с начальным положением частицы.
? 7. Частица с зарядом q и массой m влетает в электрическое поле плоского конденсатора в точке, находящейся посередине между пластинами (рис. 56.1). Пластины конденсатора расположены горизонтально. Расстояние между пластинами равно d, длина пластин l, напряжение между пластинами U. Начальная скорость частицы равна по модулю v0 и направлена горизонтально. а) Чему равны проекции ускорения частицы на оси координат при ее движении внутри конденсатора?
б) Как зависят от времени проекции скорости частицы? в) Как зависят от времени координаты частицы? г) Сколько времени частица будет лететь сквозь весь конденсатор, если не столкнется с его пластиной? д) При каком соотношении между указанными выше параметрами частица пролетит сквозь весь конденсатор и вылетит из него? е) Чему равен тангенс угла между скоростью частицы и горизонталью в тот момент, когда частица вылетает из конденсатора?
ж) Чему равен модуль скорости частицы, когда она вылетает из конденсатора?
? 8. Электрон влетает в конденсатор посередине между его пластинами со скоростью, направленной параллельно пластинам. Расстояние между пластинами равно 1 см, длина пластин 10 см. Начальная скорость электрона 5 * 107 м/с.
а) Какова должна быть разность потенциалов между пластинами конденсатора, чтобы электрон не пролетел сквозь весь конденсатор? б) На какую пластину в таком случае попадет электрон? в) На каком расстоянии от положительной пластины будет находиться электрон в момент вылета из конденсатора, если напряжение между его пластинами равно 100 В? г) Чему в этом случае будет равен тангенс угла между скоростью электрона и горизонталью в момент его вылета из конденсатора?
д) Как в этом случае изменится потенциальная энергия электрона за время его движения в конденсаторе? е) На сколько процентов увеличится кинетическая энергия электрона за время движения в конденсаторе?
Рассмотрим случай, когда начальная скорость частицы направлена под углом к пластинам конденсатора.
Возможные типы траектории движения частицы схематически изображены на рисунке 56.2. Для определенности мы выбрали положительно заряженную частицу.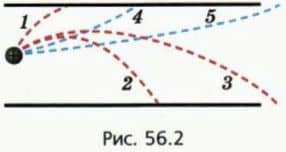 
? 9. Каков знак заряда верхней пластины конденсатора, если положительно заряженная частица движется по одной из траекторий, изображенных красным пунктиром? синим пунктиром?
3. Движение заряженного тела в электрическом поле с учетом силы тяжести
Рассмотрим теперь случай, когда надо учитывать не только силу, действующую на тело со стороны электрического поля, но и силу тяжести.
? 10. Две большие пластины заряженного плоского конденсатора расположены вертикально (рис. 56.3). Разность потенциалов между пластинами равна U, а расстояние между ними равно d. Посередине между пластинами находится шарик с зарядом q и массой m. В начальный момент шарик покоится. Через некоторое время после того, как шарик отпустили, он столкнулся с одной из пластин конденсатора.
Направим оси координат, как показано на рисунке. 56.3 а) Чему равна по модулю сила, действующая на шарик со стороны электрического поля? б) Чему равна проекция ускорения шарика на ось х? в) Через какой промежуток времени шарик столкнется с пластиной?
Каков знак заряда этой пластины? г) Насколько уменьшится высота шарика над землей к моменту столкновения по сравнению с его начальной высотой? д) Какова форма траектории шарика? е) Чему равно ускорение шарика во время движения?
ж) Чему равна скорость шарика в момент столкновения с пластиной?
Дополнительно вопросы и задания
11. Крупинка массой 10-5 г влетает в электрическое поле горизонтально расположенного плоского конденсатора в точке, находящейся посередине между пластинами. Верхняя пластина конденсатора заряжена положительно. Начальная скорость крупинки направлена горизонтально.
Длина пластин конденсатора 10 см, расстояние между пластинами 1 см, напряжение между пластинами 1 кВ. Начальная скорость пылинки 6 м/с. Заряд крупинки равен по модулю 3 * 10-12 Кл.
а) Чему равно отношение модулей силы тяжести и силы, действующей на крупинку со стороны электрического поля? При каком знаке заряда крупинки эти силы направлены одинаково? б) Чему равно и как направлено ускорение крупинки, если у нее избыток электронов? недостаток электронов?
в) При каком знаке заряда крупинки она пролетит конденсатор насквозь?
12. Заряженная частица влетает в однородное электрическое поле с начальной скоростью, перпендикулярной линиям напряженности поля. В момент вылета из поля направление ее скорости составляет угол 60º с направлением начальной скорости. Во сколько раз увеличилась кинетическая энергия частицы при движении в электрическом поле?
Считайте, что силой тяжести можно пренебречь.
(1 votes, average: 5,00 out of 5)