План-конспект урока по физике. Тема: Математический маятник. Динамика колебательного движения
Цель урока: сформировать у учащихся представление о математическом маятнике, как о модели физического маятника; на основании законов механики Ньютона получить уравнения, описывающие колебательные движения.
Ход урока
Проверка домашнего задания методом индивидуального опроса
1. Что изучает физика колебаний? По какому принципу объединены вопросы в этом разделе?
2. Особенности свободных и вынужденных колебаний. Примеры.
3. При каких условиях возникают свободные колебания? Рассмотреть на примере
Изучение нового материала
1. Физический маятник – это шарик, подвешенный на длинной нити.
2. Если пренебречь размерами шарика и рассматривать его как материальную точку, а массу и растяжение нити не учитывать, то мы получим математический маятник, модель – физического.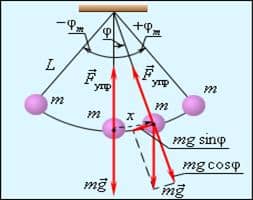 
3. Какие силы действуют на шарик? F̄T= mg и Fупр- направлена вдоль нити. Силу сопротивления будем считать ничтожно малой и не будем ее учитывать.
4. Чтобы понять динамику движения маятника, разложим силу тяжести на две составляющие: Fn= mg QUOTE 
и Fτ=mg QUOTE 
. Сила упругости Fупр и составляющая Fn – перпендикулярны скорости маятника и сообщают ему центростремительное ускорение.
Работа этих сил = 0. Поэтому эти силы не меняют скорости маятника по модулю.
Их действие вызывает непрерывное изменение вектора скорости, так что скорость в любой момент направлена по касательной к дуге окружности.
Сила Fτ двигает маятник с нарастающей скоростью по дуге окружности вниз.
Эта сила Fτ всегда направлена к положению равновесия, уменьшается по модулю и проходя через положение равновесия становится равной нулю. Но из-за инертности маятник продолжает движение, поднимаясь вверх, а сила Fτ уже будет направлена против скорости.
Таким образом, математический маятник свободно колеблется при выведении его из положения равновесия и небольшом трении в системе.
5. Получим уравнения движения для пружинного маятника и для математического маятника.
6. Для пружинного маятника. Для математического маятника
F= ma — 2-ой закон Ньютона F=ma – 2 –ой закон Ньютона
F= — kx — закон Гука Fτ= — mg QUOTE 
составляющая силы тяжести
ma= — kx; a= — kx/m ma= — mg QUOTE ; a =- g x/L
Wn= kx2/2 Wn= mgh;
Wk= mV2/2 WK= mV2/2
7. Уравнения для ускорений просты на вид и формулируются так: ускорение прямо пропорционально координате.
Значит, смещение шарика ,колеблющегося маятника и тела на пружине от положений равновесия происходят по одному и тому же закону, хотя силы, вызвавшие эти смещения, имеют разную физическую природу.
Закрепление изученного материала
1. Какой маятник называется математическим?
2. Под действием , каких сил, происходят колебания математического маятника?
3. Пояснить уравнение для пружинного маятника.
4. Пояснить уравнение для математического маятника.
Подведем итоги урока
Домашнее задание: §20, 21, повт. §19.
(1 votes, average: 5,00 out of 5)