Прямолинейное равноускоренное движение
1. Определение прямолинейного равноускоренного движения
Поставим опыт Изучим, как скатывается шарик с наклонной плоскости. На рисунке 5.1 показаны последовательные положения шарика через равные промежутки времени.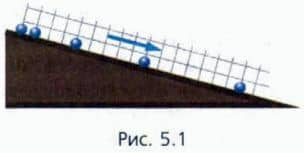 
Видно, что шарик движется неравномерно: пути, проходимые им за последовательные равные промежутки времени, увеличиваются. Следовательно, скорость шарика увеличивается.
Движение шарика, скатывающегося с наклонной плоскости, является примером прямолинейного
Прямолинейным равноускоренным движением называют прямолинейное движение, при котором скорость тела за любые равные промежутки времени изменяется на одну и ту же величину.
Прямолинейно равноускоренно может двигаться, например, автомобиль во время разгона (рис. 5.2, а). Однако непривычным может показаться то, что при торможении (рис. 5.2, б) автомобиль тоже может двигаться прямолинейно равноускоренно!
Ведь в определении прямолинейного равноускоренного движения речь идет не об увеличении скорости, а только об ее изменении.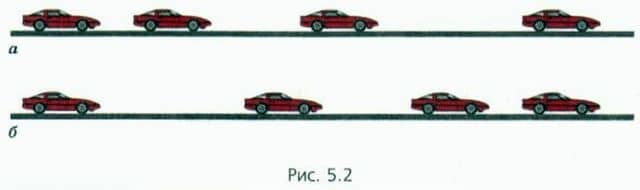 
Дело в том, что понятие ускорения в физике шире, чем в разговорном языке. В обыденной речи под ускорением понимают обычно только увеличение скорости. Мы же будем говорить, что тело движется с ускорением всегда, когда скорость тела изменяется со временем любым образом (увеличивается или уменьшается по модулю, изменяется по направлению и т. п.).
Может возникнуть вопрос: почему мы уделяем внимание именно прямолинейному равноускоренному движению? Забегая немного вперед, выдадим «секрет»: именно с таким движением мы будем очень часто иметь дело при изучении механики.
Напомним (об этом уже говорилось в курсе физики основной школы), что под действием постоянной силы тело движется прямолинейно равноускоренно. (Если начальная скорость тела равна нулю или направлена вдоль линии действия силы.) А во многих задачах по механике рассматривается именно такая ситуация. Ниже мы рассмотрим подробно ее различные варианты.
2. Ускорение
В определении прямолинейного равноускоренного движения речь идет об изменении скорости. Как определяют изменение скорости?
Обозначим 
0 скорость тела в начальный момент времени, а — скорость тела через промежуток времени t. Тогда изменение скорости за этот промежуток времени 
Эту формулу можно переписать также в виде 
На рисунке 5.3 показано, как найти вектор изменения скорости Δ в случае прямолинейного неравномерного движения.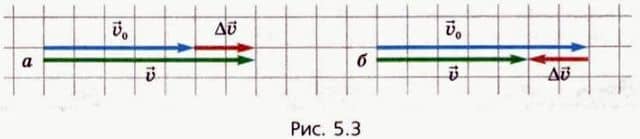 
? 1. Какому из рисунков 5.3 (а или б) соответствует увеличение скорости, а какому — уменьшение?
Введем теперь понятие ускорения.
Ускорением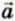 
называют отношение изменения скорости Δ к промежутку времени Δt, за который произошло это изменение: 
(Здесь в общем случае надо говорить о мгновенном ускорении, которое определяется с помощью достаточно малых промежутков времени — подобно тому, как мы определяли выше мгновенную скорость. При прямолинейном равноускоренном движении мгновенное ускорение постоянно.)
Как следует из этого определения, ускорение — векторная величина. Она характеризует скорость изменения скорости. Единицей ускорения в СИ является 1 м/с2 (читают: «метр в секунду за секунду» или «метр делить на секунду в квадрате»).
Если тело движется с таким по модулю ускорением в одном направлении, то его скорость каждую секунду увеличивается (или уменьшается!) на 1 м/с.
Когда тело падает, оно движется с ускорением, равным примерно 10 м/с2 (если можно пренебречь сопротивлением воздуха).
Рассмотрим теперь, при каком условии скорость тела увеличивается, а при каком — уменьшается. Из определения (3) следует, что 
На рисунке 5.4 мы заменили (по сравнению с рисунком 5.3) Δ на равное ему выражение 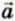Δt.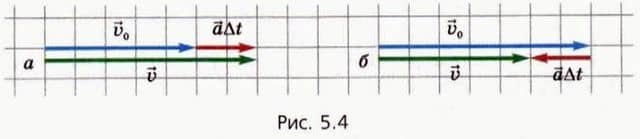 
Мы видим теперь, что скорость тела увеличивается, если ускорение направлено так же, как начальная скорость (рис. 5.4, а). Если же ускорение направлено противоположно скорости (рис.
5.4, б), то скорость тела уменьшается.
? 2. На каком из рисунков 5.2 (а или б) ускорение автомобиля направлено влево?
Выберем начальный момент времени t0 = 0, тогда Δt = t — t0 = t — 0 = t. Поскольку Δ = — 0, из формулы (4) получаем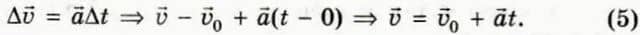 
Направим ось x вдоль траектории движения тела. Тогда
Vx = v0x + axt. (6)
Здесь vx — проекция скорости в момент времени t, v0x — проекция начальной скорости, ax — проекция ускорения.
В формуле (6) проекция начальной скорости v0x и проекция ускорения ax могут быть положительными и отрицательными. В зависимости от соотношения знаков v0x и ax модуль скорости тела будет увеличиваться или уменьшаться со временем.
Рассмотрим примеры.
? 3. Четыре автомобиля движутся вдоль оси x. В течение некоторого времени зависимость vx(t) выражается для них (в единицах СИ) формулами: 1) vx = 8 + 2t; 2) vx = 20 — 4t; 3) vx = -10 + t; 4) vx = -15 — 3t. а) Чему равны проекции начальной скорости и ускорения каждого автомобиля? б) Какие автомобили разгоняются, а какие — тормозят?
в) Скорость какого автомобиля наибольшая по модулю в момент времени t = 2 с? наименьшая?
Выполнив это задание, вы заметите, что скорость тела увеличивается по модулю, если проекция начальной скорости и проекция ускорения имеют одинаковые знаки (обе положительные или обе отрицательные).
Если же проекции начальной скорости и ускорения имеют разные знаки, то скорость тела сначала уменьшается по модулю. В некоторый момент скорость тела станет равной нулю, после чего (если ускорение останется прежним) направление скорости изменится на противоположное и модуль скорости тела начнет увеличиваться. Далее мы рассмотрим это на примере тела, брошенного вертикально вверх.
3. График зависимости скорости от времени
Из формулы (6) следует, что при прямолинейном равноускоренном движении проекция скорости vx линейно зависит от времени t. Поэтому график зависимости vx(t) — отрезок прямой.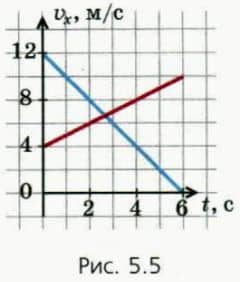 
На рисунке 5.5 изображены графики зависимости проекции скорости от времени для синего и красного автомобилей, движущихся вдоль оси x. а) Какой из автомобилей тормозит? Чему равен модуль его ускорения? б) У какого автомобиля модуль ускорения меньше?
Чему он равен? в) Запишите зависимость vx(t) для каждого автомобиля. г) Используя эту запись, найдите момент времени, когда скорости автомобилей станут равными.
Проверьте полученный ответ по приведенным графикам.
? 5. На рисунке 5.6 изображены графики зависимости проекции скорости от времени для тел, движущихся вдоль оси x.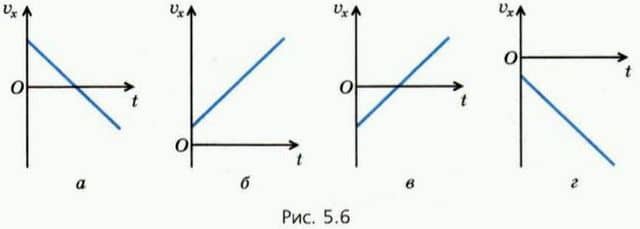 
а) Какие графики описывают движение тела, скорость которого все время увеличивается по модулю? б) На каких графиках v0x и ax имеют разные знаки?
в) Какие графики описывают случаи, когда направление скорости тела изменяется на противоположное? г) Начертите для всех изображенных случаев графики зависимости модуля скорости от времени.
? 6. Зависимость проекции скорости от времени для первого тела выражается в единицах СИ формулой v12 = 6 — Зt, а для второго — формулой v2x = 2 + t. а) Изобразите графики vx(t) для каждого тела. б) В какой момент скорости тел равны (по модулю и по направлению)? в) В какие моменты скорости тел равны по модулю?
Дополнительные вопросы и задания
7. От платформы отправляется поезд на восток. В это же время у соседней платформы тормозит поезд, идущий на запад. Сделайте схематический рисунок, на котором покажите направления скорости и ускорения каждого поезда.
8. Как направлено ускорение лифта, когда он: а) начинает двигаться с первого этажа? б) тормозит на верхнем этаже? в) тормозит на третьем этаже, двигаясь вниз? г) начинает движение на третьем этаже, двигаясь вверх?
Движение лифта при разгоне и торможении считайте равноускоренным.
9. Автомобиль трогается с места в направлении на север и набирает скорость 72 км/ч за 40 с. Движение автомобиля считайте прямолинейным равноускоренным. а) Как направлено ускорение автомобиля? б) Чему равно ускорение автомобиля по модулю?
в) Начертите график зависимости проекции скорости автомобиля от времени. г) Какой была скорость автомобиля через 10 с после начала движения?
(1 votes, average: 5,00 out of 5)