Уравнение состояния идеального газа
Уравнение состояния. Мы детально рассмотрели поведение идеального газа с точки зрения молекулярно-кинетической теории. Была определена зависимость давления газа от концентрации его молекул и температуры (формула 2.10). На основе этой зависимости можно получить уравнение, связывающее все три макроскопических параметра P, V и T, характеризующие состояние данной массы достаточно разреженного газа.
Это уравнение называют уравнением состояния идеального газа.
Подставим в уравнение (2.10) P = nkT выражение для концентрации газа. Учитывая
где NA — постоянная Авогадро, M — масса газа, M — его молярная масса.После подстановки (3.1) в (2.10) будем иметь: 
Произведение постоянной Больцмана K и постоянной Авогадро NA называют универсальной газовой постоянной и обозначают буквой R:
R = kNA = 1,38 * 10-23 * 6,02 * 1023 Дж/(моль * К) = 8,31 Дж/(моль * К). (3.3)
Подставляя в уравнение (3.2) вместо произведения KNA универсальную газовую постоянную R, получим уравнение состояния для произвольной массы идеального газа: 
Единственная величина в этом уравнении зависящая от рода газа, — это его молярная масса.
Из уравнения состояния (3.4) вытекает связь между давлением, объемом и температурой идеального газа в двух любых состояниях.
Если индексом 1 обозначить параметры, относящиеся к первому состоянию, а индексом 2 — параметры, относящиеся ко второму состоянию, то согласно уравнению (3.4) для данной массы газа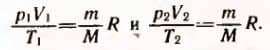 
Правые части этих уравнений одинаковы.
Следовательно, должны быть равны и их левые части: 
Уравнение состояния в форме (3.5) носит название уравнения Клапейрона и представляет собой одну из форм записи уравнения состояния. (Клапейрон Б. П. (1799-1864) — французский физик; в течение десяти лет работал в России.)
Уравнение состояния в форме (3.4) было впервые получено великим русским ученым Д. И. Менделеевым. Поэтому его называют уравнением Менделеева-Клапейрона.
Менделеев Дмитрий Иванович (1834-1907) — великий русский ученый, создатель периодической системы элементов — одного из самых глубоких обобщений в науке.
Д. И. Менделееву принадлежат важнейшие работы по теории газов, взаимным превращениям газов и жидкости (открытие критической температуры, выше которой газ нельзя превратить в жидкость). Передовой общественный деятель, Д. И. Менделеев много сделал для развития производительных сил России, использования полезных ископаемых и развития химического производства.
Экспериментальная проверка уравнения состояния. В справедливости уравнения состояния в форме (3.5) можно убедиться с помощью прибора, изображенного на рисунке 31.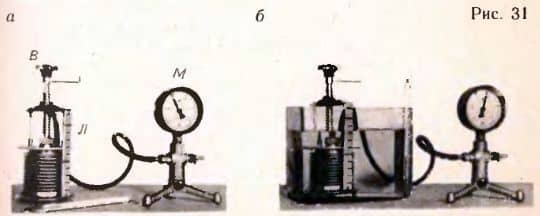 
Герметический гофрированный сосуд с манометром М, регистрирующим давление внутри сосуда.
При вращении винта В объем сосуда меняется. Об объеме можно судить с помощью линейки Л. Температура газа в сосуде равна температуре окружающего воздуха и регистрируется термометром. Измеряя давление P, температуру T и объем V газа в начальном состоянии (рис.
31, а), можно вычислить отношение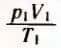 
(надо помнить, что T — это абсолютная температура, а не температура по шкале Цельсия).
После этого нужно изменить объем сосуда нагреть газ, поместив сосуд в горячую воду (рис. 31, б). Измерив снова давление газа p2, объем V2 и температуру T2, можно вычислить отношение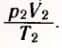 
.
В пределах точности, обеспечиваемо экспериментальной установкой, уравнение состояния (3.5) выполняется. Лишь при давлениях в тысячи атмосфер отклонения результатов эксперимента от предсказываемых уравнением состояния идеального газа, становятся существенными. Плотные газы нельзя даже приближенно считать идеальными.
(1 votes, average: 5,00 out of 5)