Абсолютная температура и средняя кинетическая энергия молекул
1. Основное уравнение молекулярно-кинетической теории
Идеальный газ. Если потенциальной энергией взаимодействия молекул в газе можно пренебречь по сравнению с кинетической энергией их хаотического движения, то можно считать, что вся внутренняя энергия газа — это сумма кинетических энергий его молекул. Такую упрощенную модель реального газа называют идеальным газом.
Молекулярно-кинетическая теория идеального газа объясняет свойства газов, рассмотренные в предыдущем параграфе.
Согласно этой теории давление газа обусловлено
Поставим опыт Будем сыпать на лист тонкого картона песок (рис. 41.1).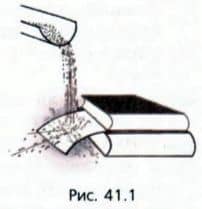 
Мы увидим, что лист картона согнется, будто на него действует постоянная сила, хотя его деформация обусловлена ударами отдельных песчинок. Таким образом, частые удары мелких частиц создают постоянную силу.
Исходя из того, что давление газа создается ударами молекул, немецкий физик Рудольф Клаузиус вывел соотношение 
Где p — давление газа, n — концентрация его молекул, m0 — масса молекулы,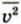 
— среднее значение квадрата скорости молекул, которое определяется формулой 
Здесь N — число молекул в газе.
Уравнение (1) называют основным уравнением молекулярно-кинетической теории идеального газа.
Запишем это уравнение с учетом того, что средняя кинетическая энергия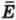 
поступательного движения молекулы связана со средним квадратом ее скорости 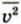соотношением 
(Если молекула состоит более чем из одного атома, у нее есть также кинетическая энергия вращательного движения. Расчет, выходящий за рамки нашего курса, показывает, что при нахождении давления газа ее учитывать не нужно.)
Отсюда следует, что m0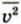 = 2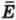. Подставляя это выражение в формулу (1), получаем другую форму записи основного уравнения молекулярно-кинетической теории идеального газа: 
Значение основного уравнения молекулярно-кинетической теории идеального газа состоит в том, что оно выражает макроскопический параметр (давление газа) через микроскопические параметры — концентрацию молекул, массу молекулы и средний квадрат скорости или среднюю кинетическую энергию молекул.
Вывод основного уравнения
План наших действий таков.
- Найдем число ударов молекул о стенку сосуда за короткий промежуток времени ∆t. Найдем импульс, передаваемый стенке одной молекулой при ударе. Найдем импульс, передаваемый стенке молекулами за промежуток времени ∆t. Найдем силу давления, используя второй закон Ньютона в импульсной форме. Найдем давление.
Направим ось x перпендикулярно стенке сосуда, давление на которую мы рассматриваем. Ее площадь обозначим S. Предположим сначала для простоты, что у всех молекул одинаковое по модулю значение проекции скорости на ось x.
Сколько молекул ударятся о стенку за коротким промежуток времени ∆t? За этот промежуток времени молекулы пролетают по направлению к стенке или от нее расстояние, равное vx∆t (рис. 41.2). Следовательно, успеет долететь до стенки и удариться о нее половина молекул, находящихся у стенки в слое толщиной vx∆t (см. рис.
41.2).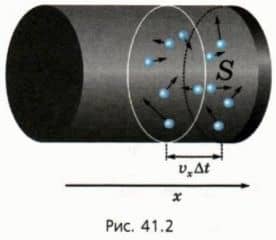 
Почему только половина?
Потому, что со стенкой столкнутся только молекулы, у которых проекция скорости vx положительна — они движутся к стенке. А к стенке и от стенки летит примерно равное число молекул.
? 1. Докажите, что в объеме слоя толщиной vx∆t и площадью S находится nSvx∆t молекул, а число Z ударов молекул о стенку за время ∆t выражается формулой
Какой импульс передает стенке при ударе одна молекула? Перед ударом проекция скорости молекулы равна vx, а после дара она равна — vx (молекула летит от стенки). Поэтому для одуля импульса, переданного стенке одной молекулой, получаем:
2m0vx.
Чему равен импульс, переданный стенке молекулами за время ∆t? Для ответа на этот вопрос надо просто умножить число Z ударов молекул на импульс, передаваемый одной молекулой. Мы получим:
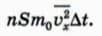В этой формуле мы учли, что на самом деле молекулы движутся с различными скоростями, поэтому в ней стоит среднее значение квадрата проекции скорости.
С какой силой газ давит на стенку? Согласно второму закону Ньютона, записанному в виде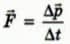 
(см. § 25), сила 
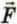давления газа равна отношению импульса, переданного стене за время ∆t, к этому промежутку времени. Следовательно,
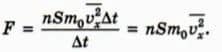Чему равно давление газа на стенку? По определению, давление p равно силе давления F, деленной на площадь поверхности S, на которую действует эта сила.
Следовательно,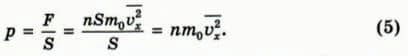 
По теореме Пифагора (в трехмерном пространстве) квадрат модуля скорости равен сумме квадратов проекций скорости:
V2 = vx2 + vy2 + vz2.
Учтем, что все направления скоростей молекул равновероятны. Поскольку молекул очень много и их движение хаотично, то средние значения квадратов проекций скорости молекул на оси координат x, y и z равны: 
Выполнив усреднение (см. формулу (2)), получим: 
Из формул (6) и (7) следует, что
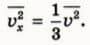Подставляя это выражение в формулу (5), получаем: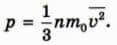 
Это и есть основное уравнение молекулярно-кинетической теории идеального газа.
2. Связь между температурой и средней кинетической энергией молекул
Напишем теперь рядом основное уравнение молекулярно-кинетической теории и уравнение состояния идеального газа в удобной для сравнения форме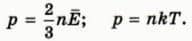 
Левые части этих уравнений совпадают. Значит, их правые части равны.
Приравнивая их, получаем: 
Эта формула раскрывает физический смысл абсолютной температуры:
Абсолютная температура является мерой средней кинетической энергии движения молекул.
Таким образом, температура является энергетической характеристикой газа.
Обратите внимание: средняя кинетическая энергия поступательного движения молекул газа зависит только от абсолютной температуры. Она не зависит ни от массы молекул, ни от давления газа. Например, молекулы кислорода и водорода при одинаковой температуре имеют одинаковые средние кинетические энергии поступательного движения (независимо от того, равны ли давления этих газов).
? 2. В воздухе содержится небольшое количество аргона (молярная масса 40 * 10-3 кг/моль) и неона (молярная масса 20 * 10-3 кг/моль). Чему равна средняя кинетическая энергия молекул каждого из этих газов при нормальных условиях? Есть ли в условии задания лишние данные? (Это одноатомные молекулы)
3. Скорости молекул
Среднеквадратичной скоростью молекул называют корень квадратный из среднего квадрата скорости молекул: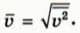 
Ее можно использовать для оценки среднего значения модуля скорости молекул. (Расчет, выходящий за рамки нашего курса, показывает, что среднее значение модуля скорости примерно равно среднеквадратичной скорости.)
Среднеквадратичную скорость молекул газа можно выразить через микроскопические параметры газа: абсолютную температуру T и молярную массу M, а также через давление p и плотность ρ.
? 3. Объясните, почему справедлива формула
? 4. Чему равны среднеквадратичные скорости молекул водорода, кислорода и радона при комнатной температуре?
Обратите внимание: при одной и той же температуре среднеквадратичные скорости молекул разных газов не равны это следствие того, что у них одинаковая средняя кинетическая энергия. Чем меньше масса молекулы, тем больше ее среднеквадратичная скорость при той же температуре.
? 5. Объясните, почему справедлива формула
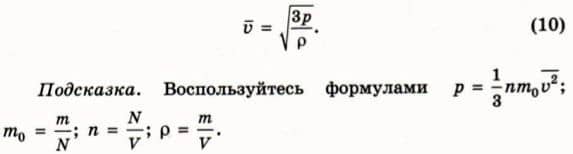
? 6. В сосуде объемом 10 л находится 14 г азота. Давление в сосуде 2 * 105 Па. Чему равна среднеквадратичная скорость молекул газа?
Есть ли в условии лишние данные?
Выполнив это задание, вы убедитесь, что молекулы действительно движутся со скоростями артиллерийских снарядов!
Измерение скоростей молекул
Значения скоростей молекул, предсказываемые молекулярно-кинетической теорией, казались некоторым ученым слишком большими, что было одним из возражений против этой теории.
В начале 20-го века немецкий физик Отто Штерн поставил опыт, в котором скорости молекул были измерены непосредственно. Вдоль общей оси двух жестко соединенных цилиндров А и В расположена покрытая серебром проволока (рис. 41.3).
Воздух из пространства между цилиндрами откачан. Проволоку нагревают электрическим током, вследствие чего атомы серебра начинают испаряться. Из цилиндра А они могут вылететь только через узкую щель.
В результате через некоторое время на внутренней поверхности цилиндра В появлялась узкая серебряная полоса 1 точно напротив щели.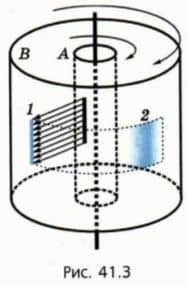 
Затем ток выключали, раскручивали соединенные цилиндры вокруг их общей оси и снова включали ток. На этот раз вместо узкой полосы напротив щели возникала довольно широкая и к тому же смещенная полоса 2.
Чем же обусловлены смещение полосы и ее расширение?
Смещение полосы было обусловлено тем, что за то время, пока атомы серебра пролетали от щели в цилиндре А до поверхности цилиндра В, сами цилиндры успевали повернуться на заметный угол.
Расширение же полосы было обусловлено тем, что скорости атомов при одной и той же температуре различны. Поэтому можно говорить только о средних значениях модуля скорости или о среднеквадратичной скорости.
Результаты опыта Штерна полностью подтвердили предсказания молекулярно-кинетической теории. 
Дополнительные вопросы и задания
7. Температура воздуха повысилась от 0 ºС до 20 ºС. На сколько процентов увеличилась при этом: а) средняя кинетическая энергия молекул в воздухе? б) среднеквадратичная скорость молекул?
8. При нагревании водорода от 300 К до 1350 К все его молекулы распались на атомы. а) Во сколько раз увеличилась средняя кинетическая энергия частиц? б) Во сколько раз увеличилась среднеквадратичная скорость частиц?
9. При повышении температуры газа на 900 К среднеквадратичная скорость молекул газа увеличилась в 2 раза. Чему равна начальная температура газа?
10. На Луне есть атмосфера, хотя и очень разреженная. Когда поверхность Луны не освещена Солнцем, концентрация газа вблизи поверхности Луны составляет 2 * 105 м-3. Температура газа при этом равна -150 ºС. а) Чему равно давление газа? б) Во сколько раз это давление меньше земного атмосферного давления?
в) Во сколько раз средняя кинетическая энергия молекул этого газа меньше средней кинетической энергии молекул при нормальных условиях? г) Во сколько раз среднеквадратичная скорость молекул газа на поверхности Луны меньше среднеквадратичной скорости молекул того же газа при нормальных условиях?
11. В первом сосуде содержится гелий, а во втором — кислород. Температура гелия равна -100 ºС. При какой абсолютной температуре кислорода: а) средняя кинетическая энергия молекул кислорода равна средней кинетической энергии молекул гелия?
б) среднеквадратичная скорость молекул кислорода равна среднеквадратичной скорости атомов гелия?
(1 votes, average: 5,00 out of 5)