Основное уравнение молекулярно-кинетической теории газов
Вычислим с помощью молекулярно-кинетической теории давление газа. Вывод формулы для давления не очень сложный, но довольно громоздкий. Разобьем его на отдельные этапы. Пусть газ находится в прямоугольном сосуде ABCD, одна из стенок которого представляет собой поршень CD, способный перемешаться без трения (рис.
21). Причем газ и сосуд имеют одинаковые температуры.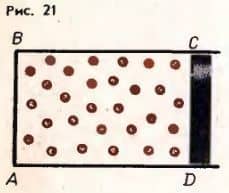 
Вычислим давление газа на поршень CD, имеющий площадь S. Поверхность поршня расположена перпендикулярно оси Ox. Давление газа
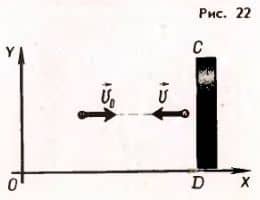
Столкновение молекулы с поршнем.Рассмотрим вначале случай, когда скорость v0 молекулы до соударения с поршнем (рис. 22) перпендикулярна поверхности поршня. Молекулы в нашей модели это твердые шарики. При столкновениях со стенкой они отскакивают от нее без изменения кинетической энергии. Подобные соударения называют абсолютно упругими.
При этом модуль скорости не меняется, а направление движения меняется на противоположное: v = — v0. Изменение импульса молекулы равно:
M0v — m0v0 = m0v — (-m0v) = 2m0v.
Если же скорость молекулы направлена под произвольным углом к поршню (рис. 23), то при столкновении молекулы с поршнем проекция v0x ее скорости на направление, перпендикулярное поверхности поршня, меняет знак vx = — v0x, а проекция v0y и v0z скоростей на направления, параллельные поверхности поршня, остаются без изменения: vy = v0y и vz = v0z. То же самое происходит с мячом при столкновении с гладкой стенкой, если считать это столкновение абсолютно упругим.
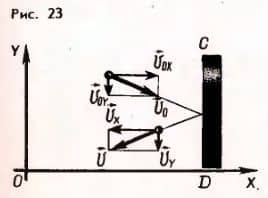Изменение проекции импульса молекулы на ось Ox равно:
M0vx — m0v0x = m0vx — (-m0vx) = 2m0vx. (1.13)
Согласно закону сохранения импульса суммарный импульс молекулы и поршня остается неизменным. Это означает, что модуль изменения импульса поршня равен модулю изменения импульса молекулы. Иначе говоря, при столкновении молекулы с поршнем поршню передается импульс, модуль которого равен 2m0|vx|.
Согласно второму закону Ньютона изменение импульса тела равно импульсу силы — произведению силы на время ее действии. Поэтому модуль импульса силы, действующей на поршень со стороны молекулы за время удара, равен 2m0|vx|.
Число соударений молекул с поршнем. Для того чтобы вычислить импульс силы, действующей на поршень со стороны всех молекул, необходимо подсчитать число соударений молекул с поршнем за некоторый интервал времени ∆t, много больший времени столкновения с поршнем одной молекулы. (Интервал ∆t можно считать таким, что в слое толщиной |vx|∆t столкновений молекул практически не происходит, хотя число молекул и велико. Это возможно, так как среднее расстояние между молекулами много меньше средней длины свободного пробега молекул, т. е. среднего расстояния, проходимого молекулами без столкновений.)
За время ∆t поршня могут достичь только молекулы, которые находятся от него на расстоянии, не превышающем CC’ = |vx|∆t (рис. 24). Молекулы, находящиеся на больших расстояниях, не успеют долететь до поршня. Надо еще учесть, что стенки CD достигают за это время лишь те молекулы, у которых vx > 0, т е. движущиеся слева направо.
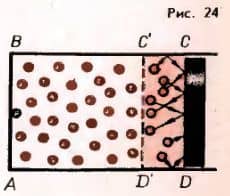Значения проекций скоростей vy и vz не влияют на достижение молекулами поршня CD. Если молекула упруго столкнется со стенкой BC или AD (рис 24), то проекция скорости vx при этом не изменится и молекула сместится вдоль оси Ox асе равно на отрезок |vx|∆t.
Выделенный объем CC’D’D равен |vx|∆t — S. Если концентрация молекул составляет n, то число их в выделенном объеме равно n|vx|∆t — S.
Вследствие хаотичности движения в среднем лишь половина молекул в выделенном объеме имеет проекцию скорости vx > 0 и движется слева направо. У другой половины молекул vx < 0 и они движутся в противоположном направлении.
Следовательно, число ударов z молекул о поршень за время ∆t, равное половине всех молекул в выделенном объеме, составляет:
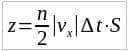(1.14)
Импульс средней силы, действующей на поршень со стороны всех молекул. Каждая молекула при соударении меняет импульс поршня на 2m0|vx|. За время ∆t все z молекул изменят его импульс на 2m0|vx|z. Согласно второму закону Ньютона модуль F∆t импульса силы, действующей на поршень, равен модулю изменения его импульса:
F∆t = z2m0|vx| = nm0Svx2∆t (1.15)
Теперь нужно учесть следующее: рассуждения велись так, как будто бы скорости всех молекул одинаковы. На самом деле скорости молекул различны и каждая из них при ударе о поршень вносит свой особый вклад в давление. Для учета этого нужно взять среднее по всем молекулам значение квадрата проекции скорости vx2 вместо vx2.
Выражение для среднего значения модуля импульса силы определится формулой F∆t = nm0Svx2∆t. 
Это и есть основное уравнение молекулярно-кинетической теории.
Давление идеального газа пропорционально произведению массы молекулы, числа молекул в единице объема и среднего квадрата скорости движения молекул.
Формула (1.17) связывает макроскопическую величину — давление, которое может быть измерено манометром, — с микроскопическими величинами, характеризующими молекулы, и является как бы мостом между двумя мирами: макроскопическим и микроскопическим. 
В следующей главе будет доказано, что средняя кинетическая энергия молекул определяется температурой газа.
1. Что называют идеальным газом в молекулярно-кинетической теории? 2. Каков механизм возникновения давления газа с точки зрения молекулярно-кинетической теории? 3. Чему равно среднее значение проекции скорости молекулы на ось Ox?
4. Дайте определение среднего значения квадрата скорости молекул. 5. Чему равно изменение импульса молекулы при ее соударении со стенкой? 6. От чего зависит число соударений молекул с поршнем площади S за время ∆t?
7. Запишите основное уравнение молекулярно-кинетической теории.
(1 votes, average: 5,00 out of 5)