Система отсчета, траектория, путь и перемещение
Механика изучает механическое движение, то есть изменение положения тел друг относительно друга с течением времени. Основная задача механики — определение положения тел в заданный момент времени, если известны положение и скорость тел в начальный момент.
Движение тел зависит от взаимодействия между ними. Но для изучения взаимодействий тел нужно овладеть понятиями, с помощью которых описывают движение тела. Это — траектория движения тела, его перемещение, скорость и ускорение.
Раздел механики, в котором рассматривают описание
1. Система отсчета
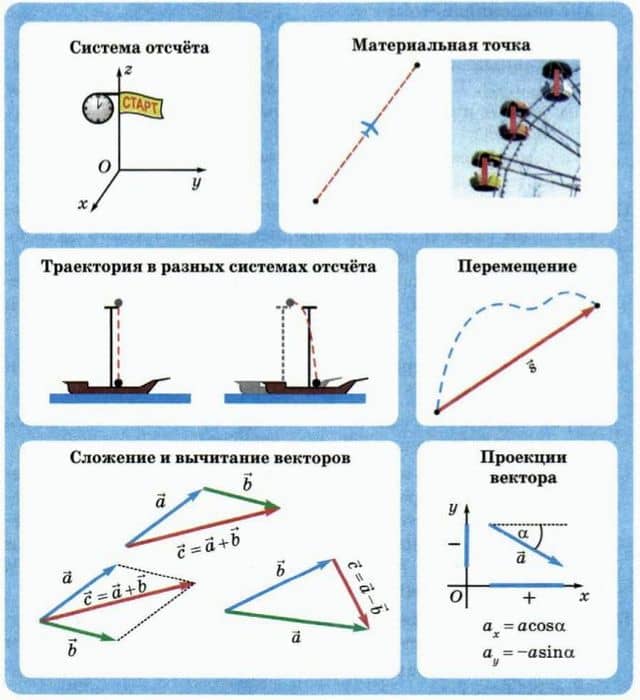
Из курса физики основной школы вы знаете, что движение относительно. Например, сидящий в кресле пассажир летящего самолета (рис. 1.1) покоится относительно самолета, однако относительно Земли он движется, причем довольно быстро.
Кроме того, он движется относительно стюардессы, идущей вдоль рядов кресел. 
Поэтому, прежде чем описывать движение тел, мы должны выбрать тело, относительно которого будем рассматривать положение всех тел в данной задаче. Это тело называют телом отсчета.
Иногда тело отсчета не указывают явно (когда из-за этого не может возникнуть недоразумений).
? 1. Что принято за тело отсчета в следующих случаях? а) Автомобиль едет со скоростью 100 км/ч. б) Стюардесса идет со скоростью 1 м/с.
в) Скорость Луны равна 1 км/с.
С телом отсчета связывают систему координат (рис. 1.2). Кроме того, для описания движения нужны часы.
Тело отсчета, связанная с ним система координат и часы образуют систему отсчета.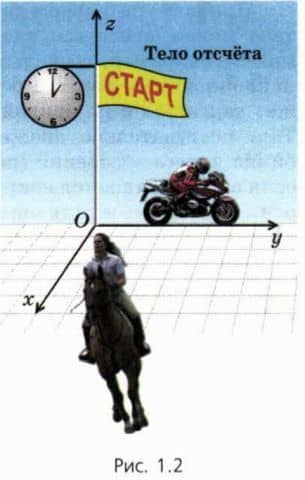 
2.
Материальная точка
Часто для описания движения тела достаточно задать движение только одной его точки. В таком случае тело мысленно заменяют одной точкой.
Тело, размерами которого в данной задаче можно пренебречь, называют материальной точкой.
Тело можно считать материальной точкой в следующих случаях.
А) Когда размеры тела малы по сравнению с расстоянием, пройденным телом. В этом случае различие в движении разных точек тела несущественно.
Например, самолет можно считать материальной точкой, если надо найти время его перелета между двумя городами (рис. 1.3). Но его нельзя считать материальной точкой при рассмотрении фигур высшего пилотажа.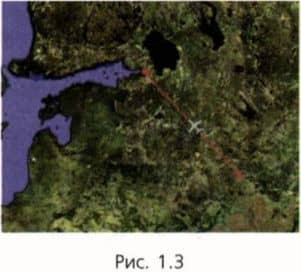 
Б) При поступательном движении тела. Так называют движение тела, при котором все его точки движутся одинаково, поэтому для описания движения тела можно задать движение только одной его точки. При поступательном движении отрезок, соединяющий любые две точки тела, остается параллельным самому себе.
При поступательном движении тело может двигаться вдоль прямой — например, соскальзывать с наклонной плоскости. Но оно может двигаться и по кривой линии. Так, поступательно движется кабинка колеса обозрения (рис. 1.4), если она не вращается вокруг своей оси.
Отрезок, соединяющий середину пола кабинки с серединой ее крыши, остается все время вертикальным (на фотографии он показан красным). 
? 2. Приведите пример задачи, в которой Землю можно считать материальной точкой, и задачи, в которой нельзя.
3. Траектория, путь и перемещение
В дальнейшем мы будем рассматривать в основном такие задачи, в которых тело можно считать материальной точкой.
Когда тело движется, соответствующая ему материальная точка описывает в пространстве некоторую воображаемую линию, которую называют траекторией движения тела (или, для краткости, просто траекторией). Если тело оставляет за собой след, траектория тела становится видимой (рис. 1.5). 
На рисунке 1.5, а изображена траектория прямолинейного движения тела, а на рисунке 1.5, б — криволинейного.
Если конечная точка траектории совпадает с начальной, траекторию называют замкнутой.
? 3. Приведите свои примеры прямолинейного и криволинейного движения, а также движения по замкнутой траектории.
Зависит ли форма траектории от выбора системы отсчета?
Рассмотрим пример, предложенный Галилеем.
С вершины мачты плывущего корабля на палубу падает ядро. В системе отсчета, связанной с кораблем, траектория движения ядра — прямолинейный вертикальный отрезок (рис. 1.6, а). В системе же отсчета, связанной с Землей, ядро движется по кривой линии — параболе (рис.
1.6, б).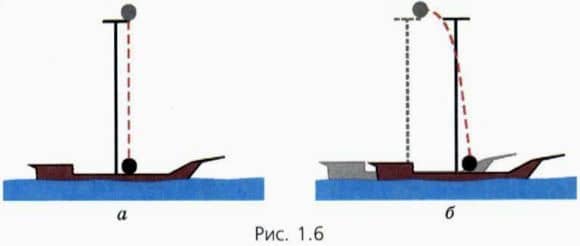 
Итак, форма траектории движения тела зависит от выбора системы отсчета.
Длину траектории называют путем, пройденным телом.
Если тело проходит какой-то участок траектории несколько раз, то путь равен длине этого участка, умноженной на число, показывающее, сколько раз тело прошло этот участок. Например, если автомобиль делает три круга по шоссе длиной 100 км, то пройденный им путь равен 300 км.
Путь является скалярной величиной (то есть характеризуется только числовым значением). Будем обозначать путь буквой l.
? 4. Какие из графиков, приведенных на рисунке 1.7, не могут отображать зависимость пути от времени? Почему?
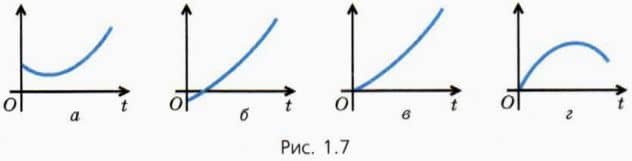
Если за любые равные промежутки времени тело проходит равные пути, движение тела называют равномерным. Оно может быть как прямолинейным, так и криволинейным.
Если же пути, проходимые телом за равные промежутки времени, не одинаковы, движение называют неравномерным.
? 5. Приведите примеры равномерного и неравномерного движения — как прямолинейного, так и криволинейного.
Пусть тело (материальная точка), двигаясь по некоторой траектории, переместилось из начального положения А в положение Б (рис. 1.8).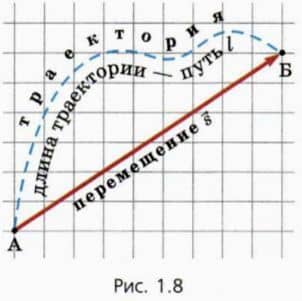 
Направленный отрезок, проведенный от начального положения тела к его положению в данный момент времени, называют перемещением 
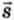тела.
Перемещение является векторной величиной, которая характеризуется неотрицательным числовым значением (модулем) и направлением.
? 6. Используя рисунок 1.8, найдите модуль перемещения материальной точки (масштаб на чертеже 1:1). Придумайте, как измерить пройденный путь, и найдите его значение. ? 7. Как движется тело, если: а) модуль его перемещения равен пройденному пути? б) перемещение равно нулю, но путь не равен нулю?
? 8. Изобразите в тетради как можно более простую траекторию движения, для которой: а) путь в 3 раза больше модуля перемещения; б) путь в π/2 раз больше модуля перемещения. ? 9. Длина минутной и секундной стрелок часов равна 10 см. В начальный момент концы стрелок совпадают. а) Чему равны модули перемещений концов этих стрелок за 20 мин?
б) Какой путь прошел конец каждой стрелки за это время?
4. Действия с векторными величинами
Векторные величины (часто для краткости их называют просто векторами) широко используют в физике: это, например, перемещение, скорость, ускорение. Векторную величину обозначают буквой со стрелкой над ней, а модуль этой величины — той же буквой, но без стрелки. Например, перемещение обозначают 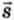, а модуль перемещения — s.
Напомним действия с векторами, уже знакомые вам из курса математики.
А) Умножение вектора на число
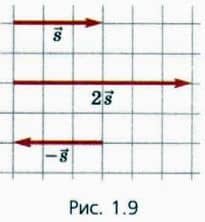
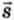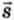При умножении вектора на число его модуль умножают на это число. Важно помнить: если это число отрицательно, то направление вектора изменяется на противоположное. На рисунке 1.9 изображены векторы , 2 и —.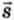 
Б) Сложение векторов
Две векторные величины складывают по правилу треугольника (рис. 1.10, а) или по правилу параллелограмма (рис. 1.10, б).
Результат сложения один и тот же, поэтому при выборе правила сложения исходят из соображений удобства.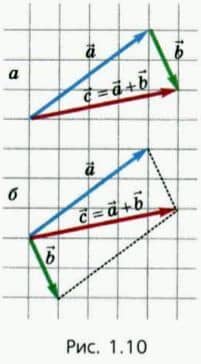 
В) Вычитание векторов
Чтобы вычесть из вектора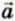 
вектор 
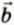, можно отложить эти векторы из одной точки и соединить направленным отрезком конец вектора 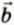с концом вектора 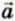(рис. 1.11). Этот направленный отрезок и есть вектор 
= — .
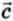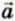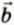Действительно, из рисунка 1.11 видно, что = + .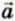 
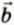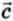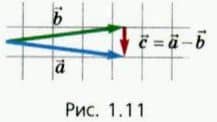
Мы намеренно выбрали случай, когда векторы 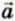и 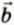равны по модулю. Обратите внимание на то, что при малом угле между такими векторами их разность представляет собой вектор, почти перпендикулярный векторам 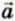и 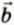. Это замечание пригодится нам в дальнейшем.
? 10. Вектор 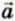направлен вертикально вверх, а вектор 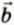по горизонтали вправо. Модуль вектора 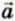равен 4, а модуль вектора 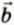равен 3. Постройте вектор = — .
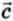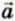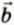Чему равен его модуль?
Проекции векторных величин
Действия с векторными величинами часто упрощаются, если использовать проекции этих величин на оси координат. (В школьном курсе геометрии проекции вектора называют координатами вектора.) Проекцию вектора обозначают той же буквой, что и сам вектор, но без стрелки и с индексом внизу, указывающим ось координат. Например, проекцию вектора 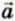на ось x обозначают ax.
Чтобы найти проекцию вектора на ось координат, проецируют изображающий этот вектор отрезок на данную ось, а затем приписывают проекции знак «+» или «-» в зависимости от того, как направлен данный вектор относительно выбранной оси. На рисунке 1.12 показано, как находить проекции векторов на оси координат x и y.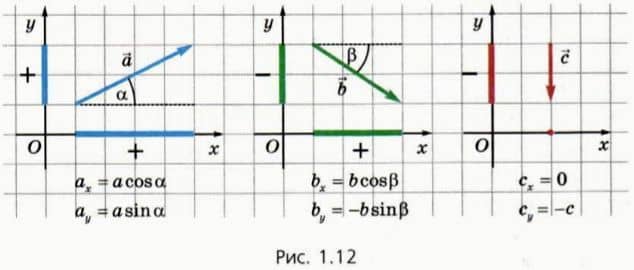 
Обратите внимание, что проекция вектора может быть положительной, отрицательной или равной нулю.
При умножении вектора на число все проекции этого вектора умножаются на то же число.
При сложении векторов их проекции складываются, а при вычитании — вычитаются.
Например, если 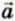= 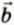+ 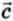, то ax = bx + cx; ay = by + cy.
? 11. Изобразите на чертеже в тетради: а) вектор, у которого обе проекции на оси координат x, y отрицательны; б) два вектора с общим началом, модули которых не равны, а проекции на ось x равны; в) два вектора с общим началом, модули которых равны, а проекции на ось y не равны.
Дополнительные вопросы и задания
12. Корабль совершил кругосветное путешествие за полгода. Является ли его траектория замкнутой в системе отсчета, связанной: а) с Землей? б) с Солнцем? Как изменились бы ответы, если бы путешествие длилось точно год?
13. Велосипедист едет по прямой дороге. Изобразите в тетради приблизительный вид траектории точки колеса велосипеда в системе отсчета, связанной: а) с велосипедистом; б) с дорогой.
14. Реактивный самолет А оставляет в небе след (см. рис. 1.5, а). Является ли этот след траекторией движения самолета А в системе отсчета, связанной: а) с Землей? б) с самолетом Б, летящим рядом с самолетом А? Поясните свои ответы.
15. Автомобиль поворачивает на 90º вправо по дуге окружности. При этом его левое переднее колесо прошло путь lл. Выразите путь lп, который прошло правое колесо, через lл и расстояние между колесами d. Найдите числовое значение lп, если lл = 10 м, d = 1,5 м. Сделайте пояснительный чертеж.
16. Вектор 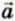имеет проекции ax = 3 см, ay = 5 см, а проекции вектора 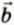равны bx = 4 см, by = -2 см. Изобразите эти векторы и найдите графически вектор 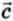= 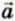— 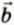. Чему равны проекции этого вектора?
17. Полярник вышел из палатки, расположенной точно на Северном полюсе, прошел 5 км по прямой, затем в направлении точно на восток 15,71 км, после этого повернул налево и шел по прямой еще 5 км. Какова форма траектории полярника? Чему равен модуль перемещения?
Сделайте в тетради пояснительный чертеж.
18. Турист переместился из пункта А в пункт В, а затем — в пункт С. Известно, что sAB = 5 км, sAC = 4 км, причем 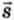BC ⊥ 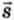AC. Чему равен sBC? Сделайте в тетради пояснительный чертеж.
(1 votes, average: 5,00 out of 5)