Движение тел относительно друг друга. Задача «встреча»
Рассмотрим, как будет выглядеть решение уже знакомой нам задачи «встреча» в системе отсчета, связанной с одним из движущихся тел.
Пусть по прямолинейной дороге навстречу друг другу едут мотоциклист и велосипедист, как показано на рис. 38. При этом относительно Земли модуль скорости мотоциклиста |vм| = 20 м/с, а модуль скорости велосипедиста — |vв| = 10 м/с. Определим, через какое время произойдет их встреча, если в момент начала наблюдения расстояние между ними l = 600 м.

Шаг
В качестве единицы длины выберем 1 м. Часы (секундомер) включим в момент начала наблюдения.
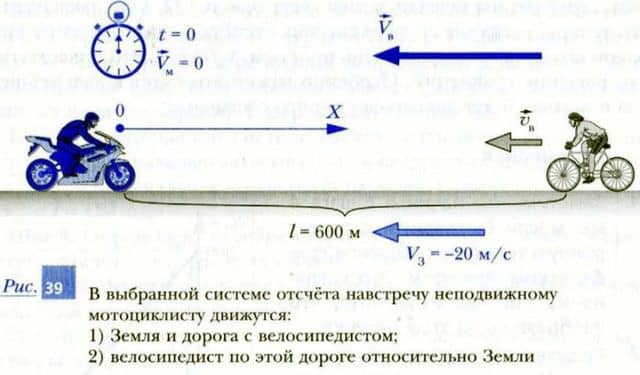
Шаг 2. Найдем начальную координату велосипедиста xв0 в момент времени t = 0. Видно, что в выбранной системе отсчета xв0 = 600 м, так как расстояние от начала отсчета (мотоциклиста) до велосипедиста l = 600 м.
Шаг 3. В выбранной системе отсчета мотоциклист неподвижен (так как он является началом отсчета и его координата все время равна xм = 0). Определим значение скорости велосипедиста. В выбранной системе отсчета Земля вместе с дорогой движутся в отрицательном направлении оси X со скоростью, имеющей значение Vз = -|vм| = -20 м/с.
Велосипедист по условию задачи движется относительно Земли также в отрицательном направлении оси X (навстречу мотоциклисту) со скоростью, имеющей значение vв = -10 м/с. Значит, относительно выбранной системы отсчета (мотоциклиста) велосипедист будет двигаться со скоростью, значение которой равно Vв = Vз + vв = (-20) + (-10) = -30 м/с. Напомним, что здесь, как и в предыдущем параграфе, мы обозначаем буквами v значения скоростей относительно Земли, а значения скоростей тел в выбранной системе отсчета — большими буквами V.
Шаг 4. Запишет законы движения мотоциклиста и велосипедиста:
Xм = 0 xв = xв0 + Vв — t = 600 — 30 — t.
Шаг 5. Представим в виде уравнения условие задачи, т. е. условие встречи мотоциклиста и велосипедиста. Как вы помните, это условие означает равенство координат движущихся навстречу друг другу тел. Поэтому
Xв = xм.
Шаг 6. Объединим полученные уравнения, присвоив каждому из них номер и название:
Xм = 0 (1) (закон движения мотоциклиста) xв = 600 — 30 — t, (2) (закон движения велосипедиста) xв = xм. (3) (условие встречи)
Шаг 7. Решим полученные уравнения, подставив в условие встречи (3) координаты xм и xв из уравнений (1) и (2):
0 = 600 — 30 — t, tвстр = t = 600/30 = 20 (с).
Таким образом, встреча произойдет через 20 с.
Обратим внимание на существенное отличие данного способа решения от способа, которым мы решали задачу «встреча» раньше. Оно заключается в том, что теперь, когда мы связали систему отсчета с одним из движущихся тел, закон его движения стал очень простым: xм(t) = 0. Это существенно упростило решение уравнений. Особенно важно это будет в дальнейшем, когда тела в задачах будут двигаться намного сложнее.
Упражнения
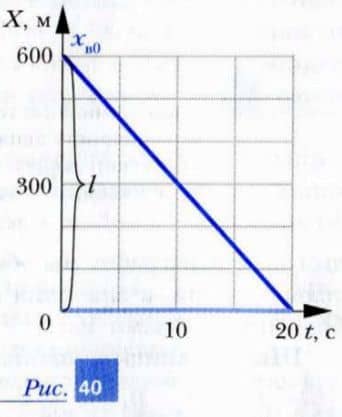
1. Заметим, что начиная с шага 4 мы могли бы решить рассмотренную только что задачу и графическим способом. Это сделано на рис. 40.
Объясните, что изображено на этом рисунке.
2. Решите задачу, изображенную на рис. 38, в системе отсчета, связанной с велосипедистом. (Особое внимание уделите вопросам: куда направить координатную ось? Куда и с какой скоростью в этой системе отсчета будут двигаться Земля и мотоциклист?)
3. Выполните упражнение 2 графическим способом начиная с шага 4.
4. Решите в общем виде задачу, условие которой изображено на рис. 38, в системе отсчета, связанной с мотоциклистом. Проведите анализ полученного решения.
