Задача «встреча». Графический способ решения
Теперь, когда мы с вами научились описывать движение тел, применим паши знания для решения практических задач. Начнем с одной из самых важных и распространенных в природе и технике задач — задачи о встрече тел. Наверняка вы неоднократно слышали о стыковках космических аппаратов, видели, как встречные поезда одновременно подъезжают к промежуточной станции, выпущенная из лука стрела попадает в цель и т. п. Все эти ситуации можно представить как движение двух точечных тел навстречу друг другу.
Задача заключается в том, чтобы определить,
Считается, что два тела встретились, если в некоторый момент времени их положения в пространстве совпали. Иначе говоря, в этот момент времени их координаты в какой-либо системе отсчета сравнялись. Поэтому для решения задачи нам понадобится ввести систему отсчета, в которой необходимо будет описать движение этих тел (в графическом или аналитическом виде).
Только таким образом мы сможем грамотно решить данную задачу.
Рассмотрим простой пример. Пусть по прямолинейной дороге навстречу друг другу одновременно начинают двигаться пешеход и велосипедист. Расстояние между ними в момент начала движения составляет l = 20 м. При этом они движутся равномерно относительно дороги навстречу друг другу со скоростями, модули которых |vп| = 1 м/с и |vв| = 3 м/с соответственно. (Мы поставили знаки модуля у скоростей движущихся тел.
Это связано с тем, что, пока не выбрана система отсчета. мы не можем сказать, у кого из них значение скорости будет положительным, а у кого — отрицательным. Другими словами, мы не можем определить, будут увеличиваться или уменьшаться их координаты в процессе движения.)
Ответим на два вопроса. Где произойдет встреча пешехода и велосипедиста? Когда (через какое время после начала движения) она состоится?
Рассмотрим каждый шаг решения задачи.
Шаг 1. Введем систему отсчета (рис. 20). В качестве тела отсчета выберем землю, а началом отсчета — место, где растет дерево, от которого начинает свое движение пешеход. Координатную ось направим вдоль дороги в направлении движения пешехода. В качестве единицы длины выберем 1 м. Будем считать пешехода и велосипедиста точечными телами.
Координата каждого из тел будет численно равна расстоянию от дерева до этого тела в заданный момент времени. Часы (секундомер) включим в тот момент, когда начинается движение.

Шаг 2. Определим значение координа пешехода и велосипедиста в момент включения секундомера. Ясно, что начальная координата пешехода xп0 (читается «икс пэ нулевое») равна 0, а велосипедиста xв0 = 20 м.
Шаг 3. Найдем значения скоростей равномерного движения тел. Из рисунка видно, что в выбранной нами системе отсчета координата пешехода в процессе движения будет увеличиваться. Следовательно, значение скорости пешехода положительно: vп = 1 м/с. Напротив, велосипедист в выбранной системе отсчета движется так, что его координата со временем уменьшается.
Поэтому значение его скорости отрицательно: vв = -3 м/с.
После того как определены начальные координаты и значения скоростей движения тел, можно переходить к описанию их движения. Для этого у нас есть несколько способов. Начнем с графического.
Шаг 4 (графический). Построим систему координат, состоящую из оси времени t и оси координаты X. Отметим начальные координаты пешехода и велосипедиста (рис. 21).
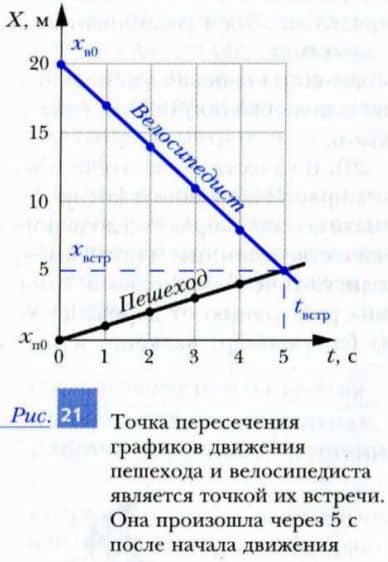
Шаг 5 (графический). Теперь от точки xп0 проведем прямую линию, описывающую зависимость координаты пешехода от времени. Поскольку по условию задачи координата пешехода за каждую секунду увеличиваются на 1 м, то это будет «поднимающаяся» прямая линия, проходящая через точки с координатами (1; 1), (2; 2), (3; 3), (4;4), (5; 5) и т. д.
График зависимости от времени координаты велосипедиста — это тоже прямая, но она исходит из точки xв0 = 20 м, расположенной на оси координаты. Координата велосипедиста со временем уменьшается на 3 м за каждую секунду. Поэтому линия, описывающая зависимость этой координаты от времени, «опускается» за каждую секунду на 3 м, т. е. эта линия проходит через точки с координатами (0; 20), (1; 17), (2; 14), (3; 11), (4; 8), (5; 5) и т. д.
Из рис. 21 следует, что прямые, описывающие зависимости координат пешехода и велосипедиста от времени, пересекаются в точке (tвстр = 5 с, xвстр = 5 м). Это означает, что через 5 секунд после начала движения координаты пешехода и велосипедиста становятся равными: xп = xв = xвстр = 5 м. Иначе говоря, в этот момент времени положения тел в пространстве совпадут, и, таким образом, в момент tвстр = 5 с в точке с координатой xвстр = 5 м произойдет встречи пешехода и велосипедиста.
Итоги
Встречей двух тел считают совпадение их положений в пространстве (равенство их координат в одной и той же системе отсчета) в некоторый момент времени.
При графическом способе решения задачи о встрече движущихся тел необходимо: ввести систему отсчета; определить начальные координаты и значения скоростей тел; построить графики движения тел; найти точку пересечения этих графиков.
Вопросы
Приведите примеры встречи двух тел. Что означает в кинематике, что два тела встретились? Перечислите шаги решения задачи «встреча».
Упражнения
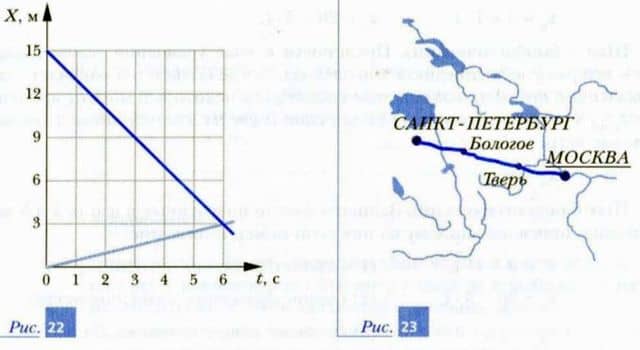
Определите графическим способом время и место встречи двух равномерно движущихся навстречу друг другу школьников, если в момент включения часов: а) расстояние между ними l = 30 м, а модули их скоростей |v1| = 3 м/с, |v2| = 3 м/с; б) расстояние между ними l = 30 м, |v1| = 1 м/с, |v2| = 4 м/с. Сформулируйте условие задачи, решение которой дано на рис. 22. Определите место встречи (город) двух равномерно движущихся поездов, которые одновременно выезжают навстречу друг другу из Москвы (|v1| = 100 км/ч) и Санкт-Петербурга (|v2| = 50 км/ч) (рис. 23). Расстояние между Москвой и Санкт-Петербургом — 600 км.